机器学习之线性回归-多因子房价预测
机器学习是一种实现人工智能的方法
从数据中寻找规律、建立关系,根据建立的关系去解决问题
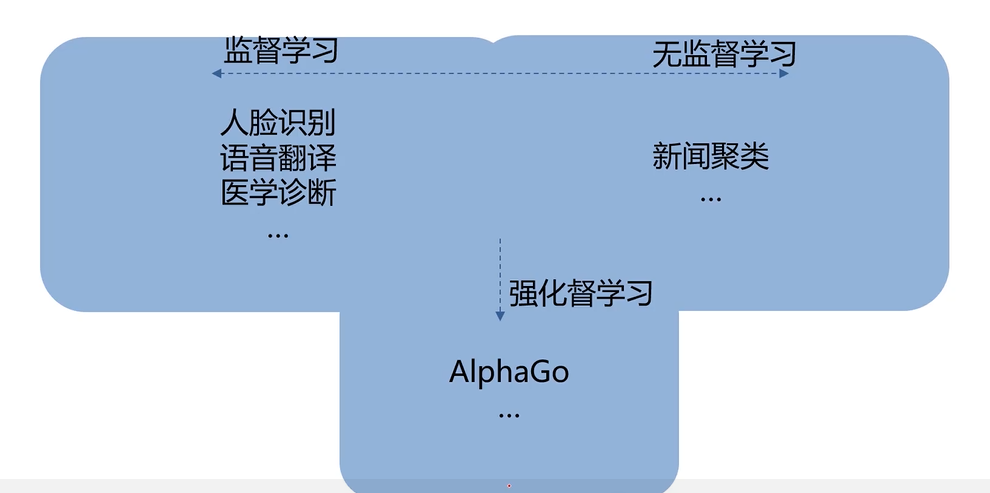
机器学习的应用场景
数据挖掘、计算机视觉、自然语言处理、证券分析、医学诊断、机器人…
实现机器学习的基本框架
将训练数据喂给计算机,计算机自动求解数据关系,在新的数据上做出预测或给出建议
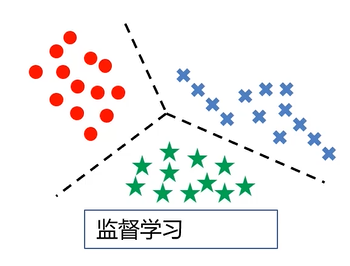
机器学习的类别
- 监督学习(Supervised Learning)
- 训练数据包括正确的结果(标签-label)
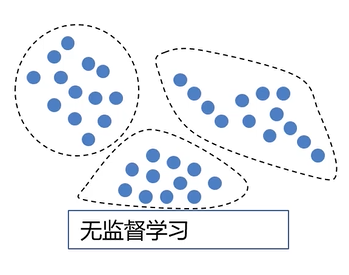
- 无监督学习(Unsupervised Learning)
- 训练数据不包括了正确的结果
- 半监督学习(Semi-supervised Learning)
- 训练数据包括少量正确的结果

强化学习


机器人行走遇到障碍物
程序初始化
根据执行效果给与奖励/惩罚(分数)
程序逐步寻找获得高分的方法
回归分析
回归分析:根据数据,确定两种或两种以上变量间相互依赖的定量关系
函数表达式:
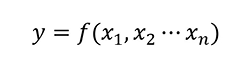
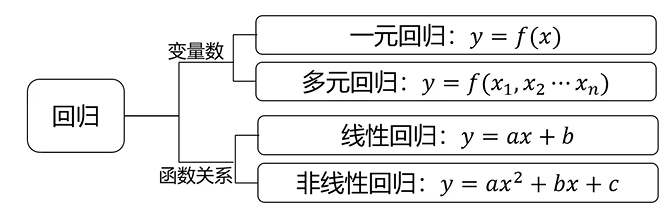
线性回归
线性回归:回归分析中,变量与因变量存在线性关系
函数表达式:
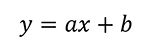
举例:
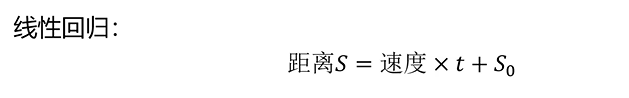

回归问题求解
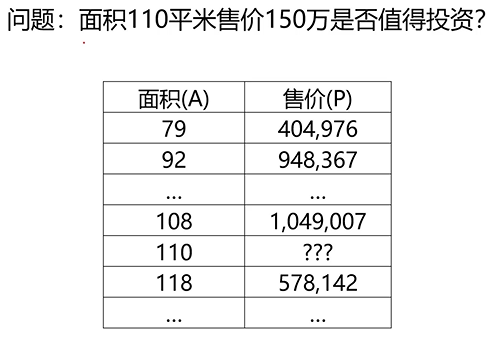
- 确定P、A间的定量关系
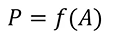
- 根据关系预测合理价格、
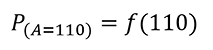
- 做出判断

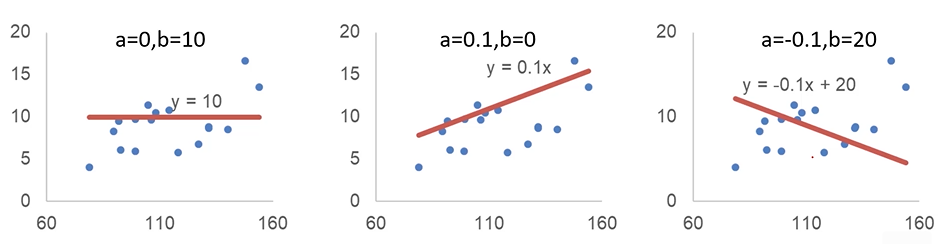
如何寻找到最合适的a、b?

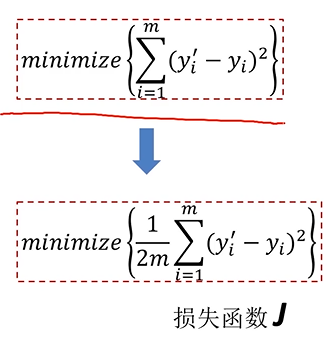
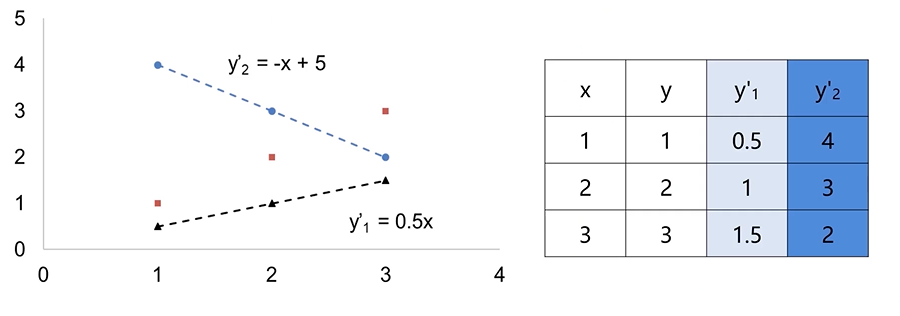
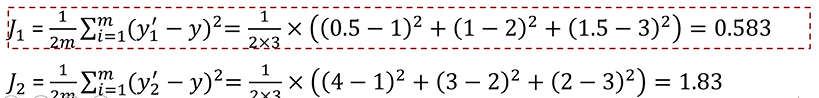


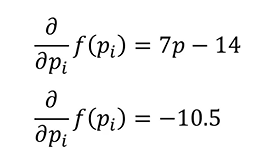
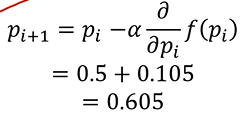
逐渐接近极小值点(p=2)

Scikit-learn
Python语言中专门针对机器学习应用而发展起来的一款开源框架(算法库),可以实现数据预处理、分类、回归、降维、模型选择等常用的机器学习算法
特点:
- 集成了机器学习中各类成熟的算法,容易安装和使用,样例丰富,教程和文档也非常详细
- 不正常Python之外的语言,不正常深度学习和强化学习
调用Sklearn求解线性回归问题
寻找a、b(y=ax+b):
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
lr_model.fit(x,y)
展示a、b:
a=lr_model.coef_
b=lr_model.intercept_
对新数据做预测:
predictions=lr_model.predict(x_new)
评估模型表现


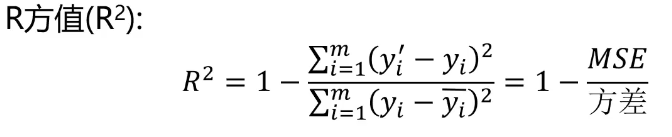
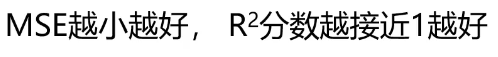
计算y与y’的均方误差(MSE)、R方值(R2_score):
from sklearn.metrics import mean_squared_error,r2_socre
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
画图对比y与y’,可视化模型表现:
from matplotlib import pyplot as plt
plt.scatter(y,y')

图像展示
画散点图
import matplotlib.pyplot as plt
plt.scatter(x,y)
多张图同时展示
fig1=plt.subplot(211)
#211 2行1列第一个
plt.scatter(x1,y1)
fig=plt.subplot(212)
plt.scatter(x2,y2)
代码演示
# 读取数据
import pandas as pd
data = pd.read_csv('generated_data.csv')
查看内容

查看数据类型和维度

print(type(data),data.shape)
赋值并打印
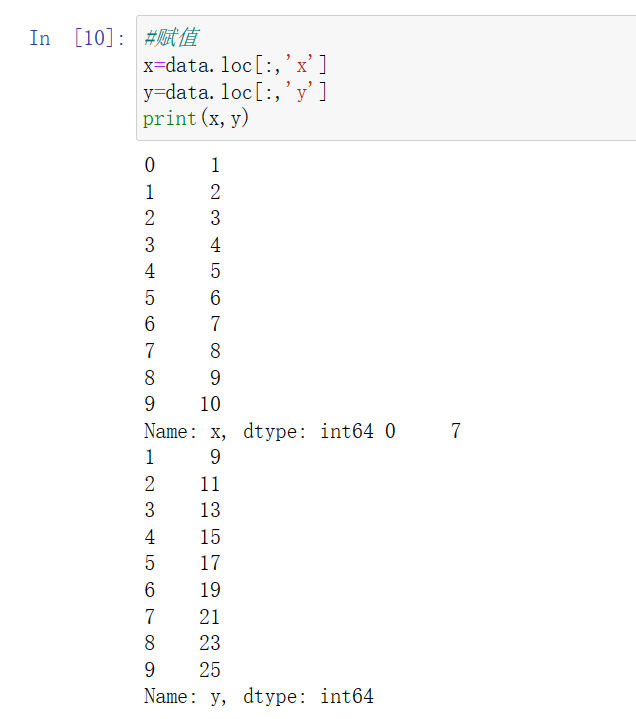
图像显示
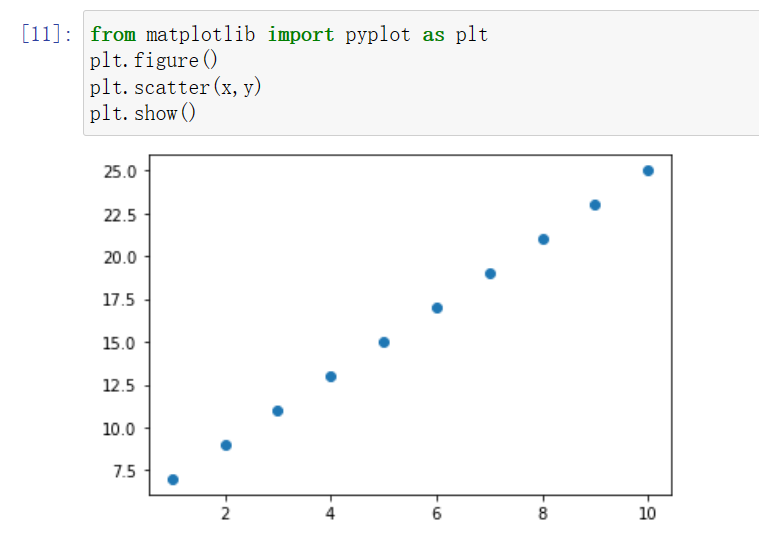
from matplotlib import pyplot as plt
plt.figure()
plt.scatter(x,y)
plt.show()
引入包,创建模型
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
更改维度
import numpy as np
x=np.array(x)
x=x.reshape(-1,1)
y=np.array(y)
y=y.reshape(-1,1)
拟合
lr_model.fit(x,y)
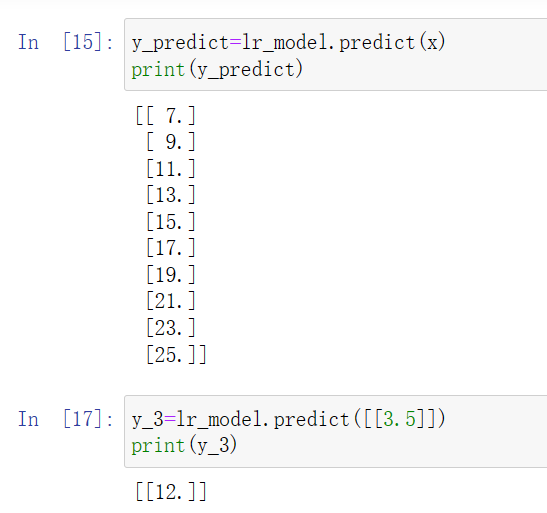
预测
y_predict=lr_model.predict(x)
print(y_predict)
y_3=lr_model.predict([[3.5]])
print(y_3)
打印a\b
a=lr_model.coef_
b=lr_model.intercept_
print(a,b)

模型评估
from sklearn.metrics import mean_squared_error,r2_score
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
print(MSE,R2)

plt.figure()
plt.plot(y,y_predict)
plt.show()
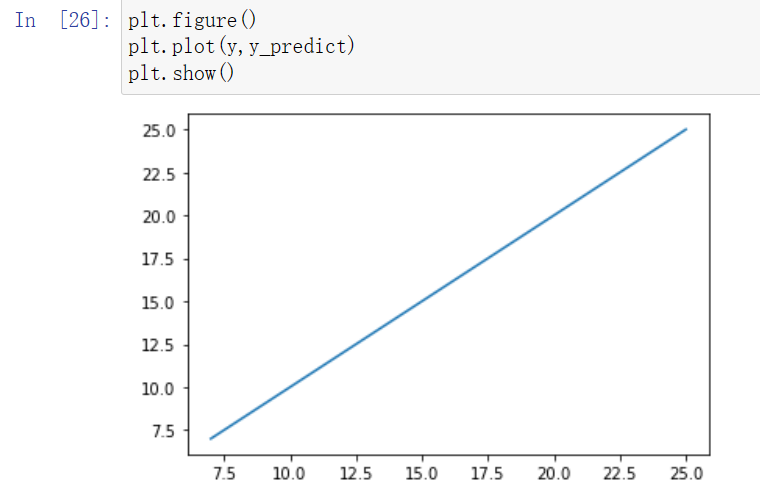
多因子房价预测
基于usa_housing_price.csv数据,建立线性回归模型,预测合理房价:
- 以面积为输入变量,建立单因子模型,评估模型表现,可视化线性回归预测结果
- 以income、house age、numbers of rooms、population、area为输入变量,建立多因子模型,评估模型表现
- 预测
Income=65000,House Age=5,Number of Rooms=5,Population=30000,size=200的合理房价
读取数据并预览
import pandas as pd
import numpy as np
data = pd.read_csv('usa_housing_price.csv')
data.head()
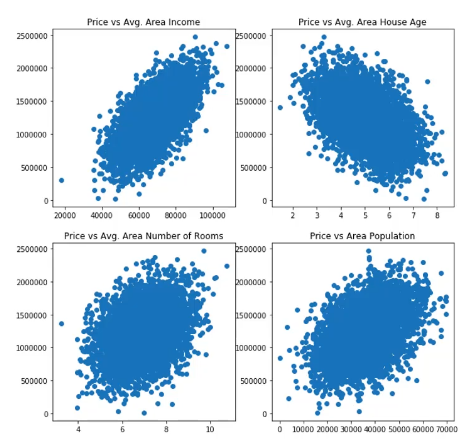
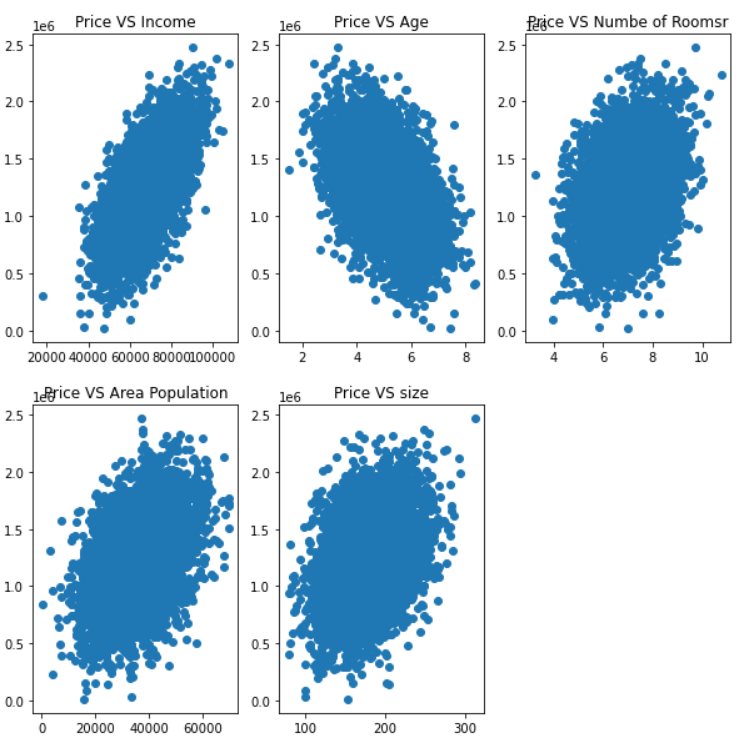
数据可视化
%matplotlib inline
from matplotlib import pyplot as plt
fig=plt.figure(figsize=(10,10))
fig1=plt.subplot(231)
plt.scatter(data.loc[:,'Avg. Area Income'],data.loc[:,'Price'])
plt.title('Price VS Income')
fig2=plt.subplot(232)
plt.scatter(data.loc[:,'Avg. Area House Age'],data.loc[:,'Price'])
plt.title('Price VS Age')
fig3=plt.subplot(233)
plt.scatter(data.loc[:,'Avg. Area Number of Rooms'],data.loc[:,'Price'])
plt.title('Price VS Numbe of Roomsr')
fig4=plt.subplot(234)
plt.scatter(data.loc[:,'Area Population'],data.loc[:,'Price'])
plt.title('Price VS Area Population')
fig5=plt.subplot(235)
plt.scatter(data.loc[:,'size'],data.loc[:,'Price'])
plt.title('Price VS size')
plt.show()
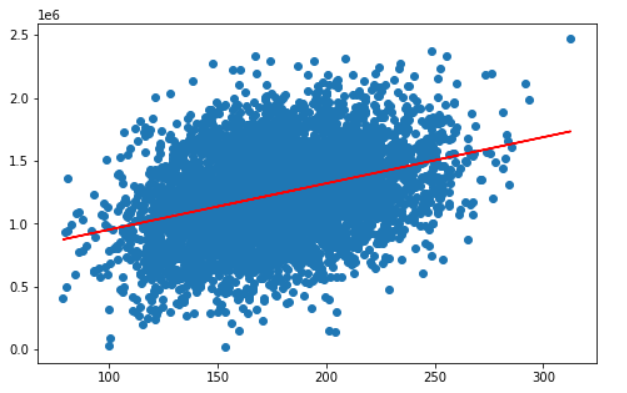
建立单因子模型
x=data.loc[:,'size']
y=data.loc[:,'Price']
x=np.array(x).reshape(-1,1)
from sklearn.linear_model import LinearRegression
LR1=LinearRegression()
LR1.fit(x,y)
预测结果
y_predict_1=LR1.predict(x)
print(y_predict_1)
模型评估
from sklearn.metrics import mean_squared_error,r2_score
mean_squared_error_1 = mean_squared_error(y,y_predict_1)
r2_score_1 = r2_score(y,y_predict_1)
print(mean_squared_error_1,r2_score_1)
可视化评估
fig6=plt.figure(figsize=(8,5))
plt.scatter(x,y)
plt.plot(x,y_predict_1,'r')
plt.show()
多因子
读取数据
X_multi=data.drop(['Price'],axis=1)
X_multi
#创建实例
LR_multi = LinearRegression()
#训练
LR_multi.fit(X_multi,y)
#模型预测
y_predict_multi=LR_multi.predict(X_multi)
print(y_predict_multi)
#评估
mean_squared_error_multi = mean_squared_error(y,y_predict_multi)
r2_score_multi = r2_score(y,y_predict_multi)
print(mean_squared_error_multi,r2_score_multi)
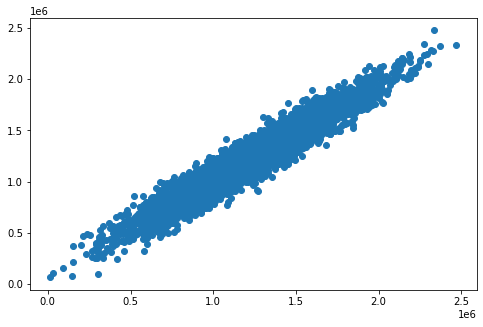
可视化
fig7=plt.figure(figsize=(8,5))
plt.scatter(y,y_predict_multi)
plt.show()
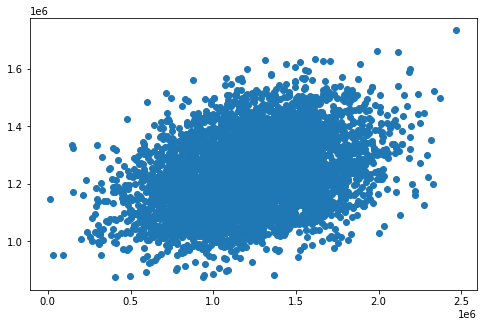
对比单因子
fig8=plt.figure(figsize=(8,5))
plt.scatter(y,y_predict_1)
plt.show()
预测
Income=65000,House Age=5,Number of Rooms=5,Population=30000,size=200的合理房价
X_test=[65000,5,5,30000,200]
X_test=np.array(X_test).reshape(1,-1)
print(X_test)
# 预测
y_test_predict=LR_multi.predict(X_test)
print(y_test_predict)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!