递归经典问题讲解

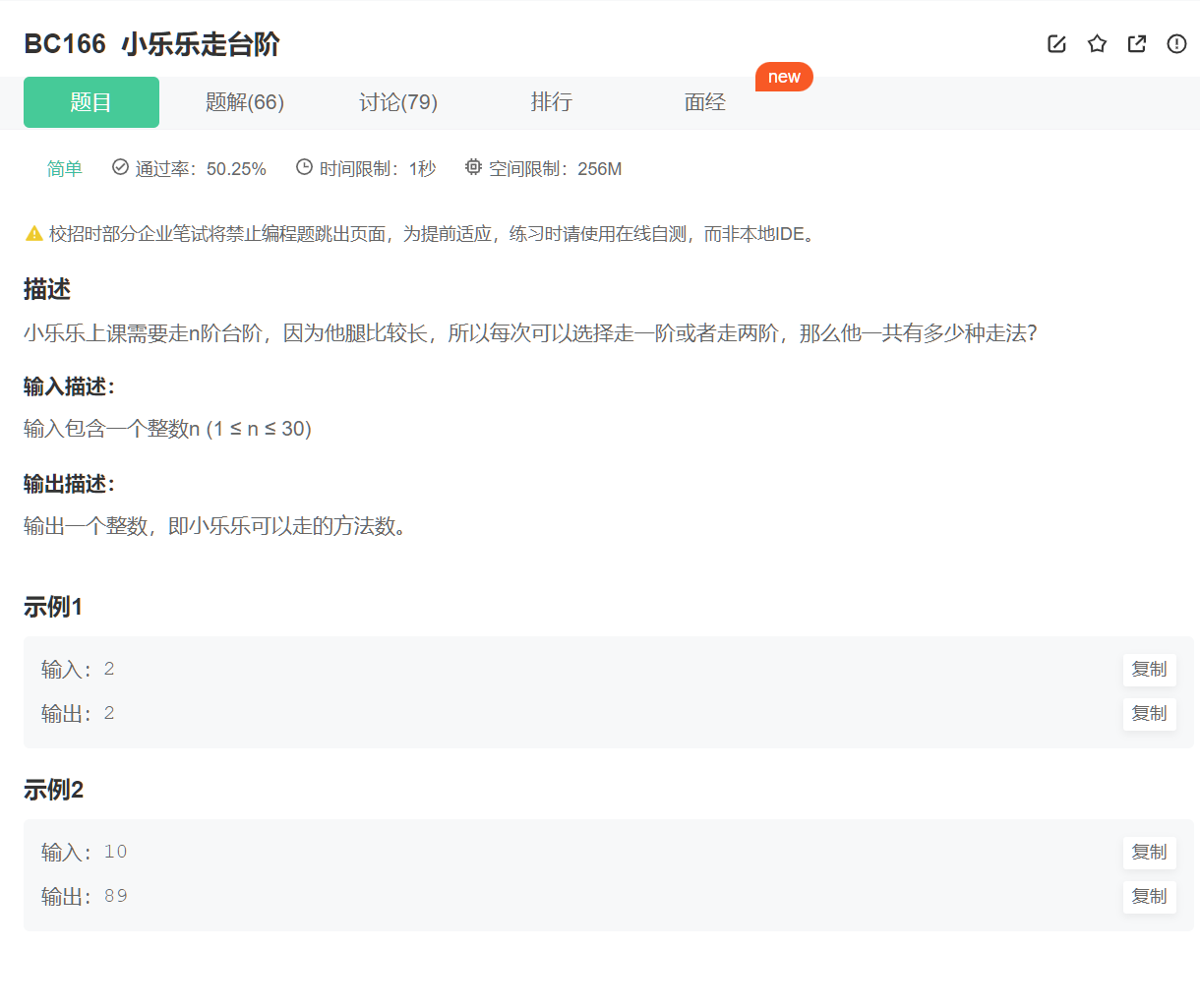
小乐乐走台阶问题

题目链接

思路讲解

? ? ? ? 这里我们假设由n阶台阶，设函数F(n)为总共的走法，即有n台阶的时候我们有F(n)种走法，我们往上递推一下，如果我们上一步是走了一阶台阶的话，就会剩下n-1台阶，就有F(n-1）种走法；如果我们上一步是走了两阶台阶的话，就会剩下n-1台阶，就有F（n-2）种走法；这样我们就得到了F(n) = F(n-1) + F(n-2)
? ? ? ?我们继续递推验证一下，F(n-1)时，有n-1个台阶，上一步要么走了一步要么走了两步，即F(n-1)=F(n-2)+F(n-3); F(n-2)时，有n-2个台阶，要么走了一步要么两步，即F(n-2)=F(n-3)+F(n-4); 以此类推…
? ? ? ?接下来要思考递归停止条件，避免出现死递归现象，所以我们来考虑递归到最后，其实就会剩下一个台阶，对应一种走法，或者剩下两个台阶，就是一步一步或二步这两种走法，所以这就是递归结束条件，递推到最后F(3)=F(1)+F(2);之后进行回归操作。

---

代码示例

#include  <stdio.h>
  
int  sum(int  n)
{
 if(n==1)
 return  1;
 if(n==2)
 return  2;
 return  sum(n-1)+sum(n-2);
}
  
int  main()
{
 int n;
 scanf("%d",&n);
 int ret = sum(n);
 printf("%d",ret);
 return  0;
}

---

汉诺塔问题

汉诺塔问题是一个经典的递归问题，最初由法国数学家Edouard Lucas提出。问题描述如下：有三根柱子A、B、C，开始时柱子A上有n个盘子，盘子从上到下按照从小到大的顺序摆放。现在要将这n个盘子从柱子A移动到柱子C，期间可以借助柱子B，但要满足以下规则：

1. 每次只能移动一个盘子；
2. 大盘子不能放在小盘子上面。

问题如下：给定n个盘子，请问有怎么把这些盘子移动到大盘子里。
输入实例如下
input：1
output:A->C

input：2
output:A->B A->C B->C

input：3
output:A->C A->B C->B A->C B->A B->C A->C

思路讲解

? ? ? ?我们从最简单的下手，如果只有一个盘子的时候，我们直接将这个盘子从A移动到C
? ? ? ?如果有两个的时候，我们需要将最上面的小盘子放在B上，然后将A剩下的大盘子放在C中，将B上的盘子放在C中就可以了。
? ? ? ?如果视频看不到，出现数据不存在的情况，重新加载或刷新一下即可。

? ? ? ?如果有三个盘子，我们就有需要将上面两个先放在B柱子上，这样A柱上最后一个盘子就可以放在C柱子上，B柱上的两个盘子便要借助A柱子依次移动到C柱上，大家可以看一下下面的移动视频：
? ? ? ?如果视频看不到，出现数据不存在的情况，重新加载或刷新一下即可。

? ? ? ?根据上面的推演，我们可以将汉诺塔问题抽象成1和n-1的问题，也就是说我们需要将除了A柱上最大的盘子之外，将上面的n-1个盘子先移动到B柱上，然后这一个最大的盘子就可以移动到C柱上，在B柱上最大的盘子不动，其上面的n-2个盘子需要移动到A盘上，最后将B柱上这个盘子移动到C盘上，以此类推…
大家可以看一下抽象出来的视频：
? ? ? ?如果视频看不到，出现数据不存在的情况，重新加载或刷新一下即可。

代码示例

#include <stdio.h>

void move(char p1, char p2)
{
	printf("%c->%c  ", p1, p2);
}

void HanNuoTa(int n,char p1,char p2,char p3)
{
	if (n == 1)
		printf("%c->%c ", p1, p3);
	else
	{
		HanNuoTa(n - 1, p1, p3, p2);
		move(p1, p3);
		HanNuoTa(n - 1, p2, p1, p3);
	}
}

int main()
{
	int n;
	while (scanf("%d", &n) != EOF)
	{
		HanNuoTa(n, 'A', 'B', 'C');
	}
	return 0;
}