计算机组成原理05：定点数除法

回忆一下计算原码乘法时我们的计算步骤，再思考一下我们手算竖式除法的步骤，发现它们都有一个共同点，就是都需要移位。不同的点在于，乘法中每一步都是加法，而显然的，除法中的每一步都是减法。

定点数除法问题分析

根据以上的背景，我们可以分析出几个定点除法的特点和问题：

1. 除法可以通过减法实现
2. 需要2n位的余数寄存器（这是因为所有的被除数的位都要参与运算，根据手工运算除法，最后留下的余数最多可能有2n位）
3. 需要判断是否够减

定点数除法算法设计

关于定点数除法的前两个特点我们可以和乘法类比，但问题在于第三点：如何判断上一步留下的差是否仍然够减？在手工除法中，我们一般通过将新的被除数和除数比大小来判断是否够减。计算机也可以通过类似的方式来实现。通过这种方式判断是否够减的定点数除法，我们称作原码回恢复余数除法。

原码恢复余数除法

在原码恢复余数除法中，一开始都假设本次运算的商为1，并且将余数减去除数，随后判断差的正负。如果为正则继续运算，如果为负数，则将除数加回去（也就是”恢复余数“），并且本次运算的商改为0。随后，根据手工除法的规律，将余数左移一位，进行下一次比较。

下面是一个原码恢复余数除法的例子：

使用原码恢复余数除法计算： 0.1001/0.1011

解：

被除数/余数            商            说明

  1001                1
- 1011
--------------------------------------------
 -0010               
  1001                0         余数为负，恢复余数，商上0
->10010               0            余数左移
-  1011              01
-------------------------------------------------
    111                         余数为正，不恢复，商上1
-> 1110
-  1011              011
-------------------------------------------------
     11                          余数为正，不恢复，商上1
->  110
-  1011              0111  
-------------------------------------------------
   -101                  
    110            0110           余数为负，恢复余数，商上0    
->  1100                           
-   1011            01101
--------------------------------------------------
    0001

故商为0.1101，余数为0.00000001

加减交替法（不恢复余数除法）

原码恢复余数除法虽然容易理解，但是使用原码恢复余数除法不容易确定恢复余数的次数，为程序设计造成了困难。使用加减交替法后，计算的次数就完全取决于被除数和除数的位数。

?加减交替法的设计如下：

1. 减去除数，然后按照2，3进行比较
2. 如果余数大于0，那么商上1，余数左移一位，减去除数
3. 如果余数小于0，那么商上0，余数左移一位，加上除数

下面是一个加减交替法的例子：

使用加减交替法计算： 0.1001/0.1011

解：

被除数/余数            商            说明

  1001                
- 1011
--------------------------------------------
  -0010                        余数为负，左移后加上除数，商上0
->-0100               0            余数左移
+ 1011              
-------------------------------------------------
   111                         余数为正，左移后减去除数，商上1
-> 1110
-  1011              01
-------------------------------------------------
     11                          余数为正，左移后减去除数，商上1
->  110
-  1011              011  
-------------------------------------------------
   -101                         余数为负，左移后加上除数，商上0    
-> -1010                           
+   1011             0110
--------------------------------------------------
    0001            01101        余数为正，商上1，结束

故商为0.1101，余数为0.00000001

使用加减交替法相比恢复余数除法，确定了计算的次数，便于使用循环计数。而且其计算方法从形式上看是非常简洁的。

除法器的设计

为了简便，我们使用加减交替法的方法来设计除法器。下面是全加器的例子：

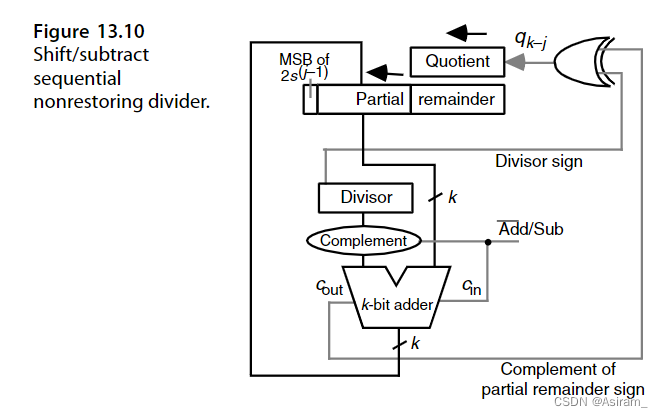
阵列除法器

阵列除法器同样基于加减交替法实现，在元件上则集成为一个可控制加减单元CAS，由一位信号P控制。当P=0时，CAS为全加器；当P=1时，CAS为全减器。

基于CAS的阵列除法器设计如下：

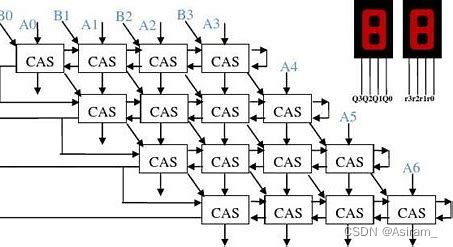
该阵列除法器使用串行除法，特点如下：

1. 使用加减交替法（不恢复余数除法）
2. 最左边的CAS输出商，决定下一位是加还是减
3. 执行完一步除法后右移一位

关于除法器的高级知识，可以参考一下知乎文章：

【硬件算法笔记13】基础除法器方案 - 知乎 (zhihu.com)