我的AI之旅开始了

?

知道重要，但是就是不动。? ? ? ? ?

今天告诉自己，必须开始学习了。

用这篇博文作为1月份AI学习之旅的起跑点吧。

从此，无惧AI，无惧编程。

AI之路就在脚下。

AI，在我理解，就是让机器变得更加智能，能够以人思考和行为的方式去实行某种操作，更大更快更强。

编程和AI的关系，就如同鱼与水的关系。

没有编程，AI就没有办法乖乖的听我们的话，做我们要它做的事。

编程，就相当于是发布一条条指令，指挥机器去干这个，去干那个。

机器就是一堆机械堆砌出来的玩意。他们没有感情，只会冷血的一条一条执行程序。

想让它为我所用，就得学编程。

所以，MATLAB，我来了。

反向学习：

利用反向学习，可以增加种群的多样性，防止种群陷入局部最优。

基本初等函数：

正弦、余弦、反正弦、反余弦、正切、余切、反正切、反余切、指数、对数、幂、以e为底的指数函数、S型函数等。

这些基本初等函数可以两两组队成为复合函数。

高斯随机游走策略：

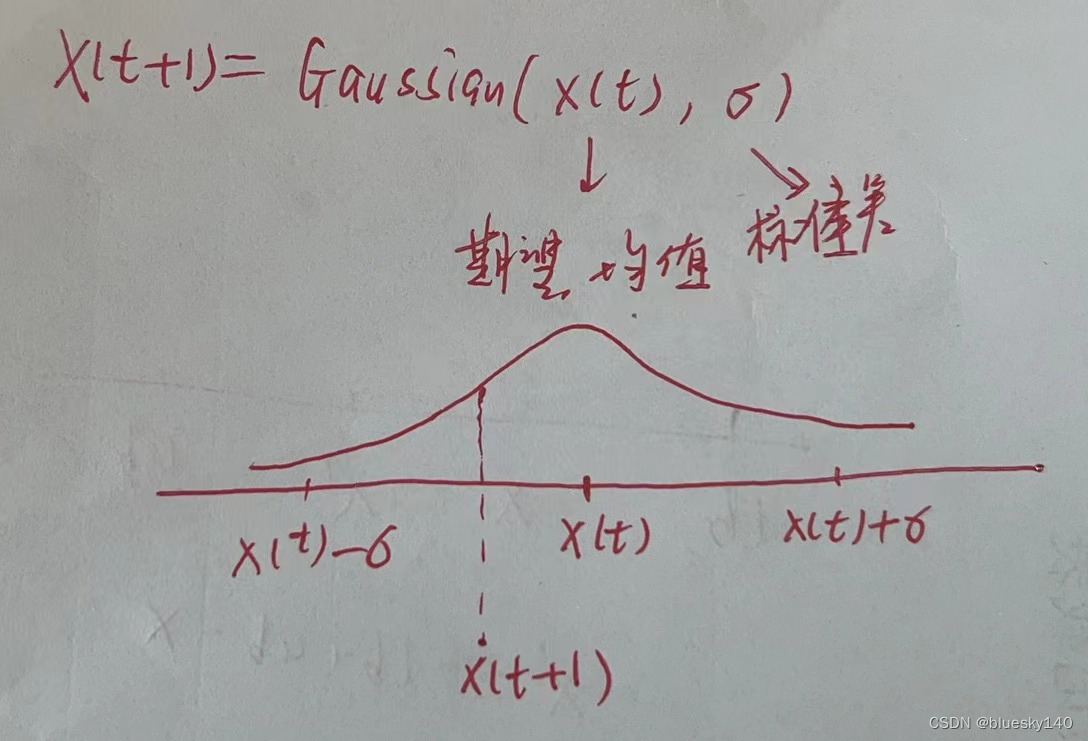
下一步位置等于上一步位置的高斯扰动。

在上一个位置的基础上，下一个位置存在于距离上一个位置左右两边距离标准差σ内存在的可能性比较大。

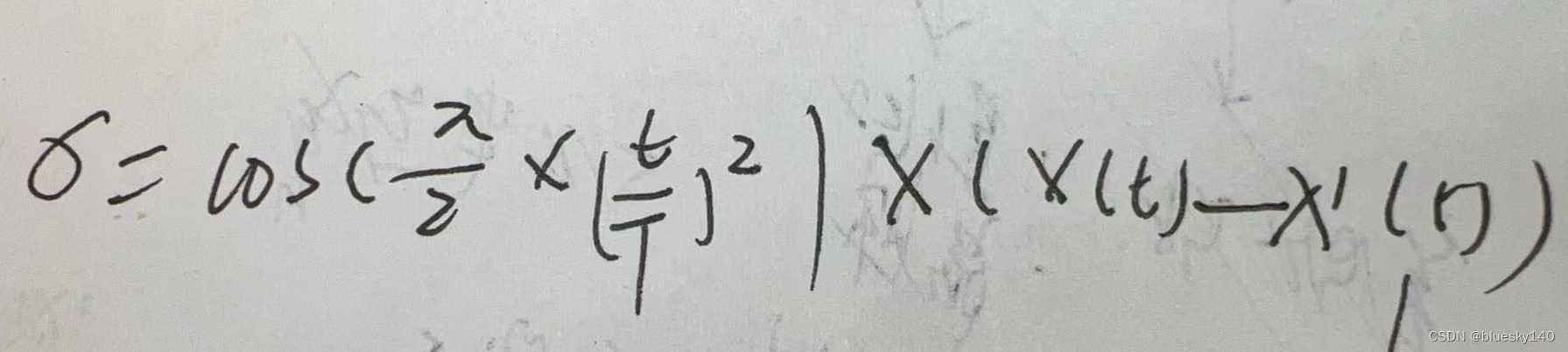
x'(t)表示最佳位置，或者平均位置，或者中位数位置。

高斯分布，也可以改成柯西分布，或者莱维分布。

1、2、5、9、13的中位数为5。

通过余弦函数，在迭代前期施加较大扰动，在迭代后期，扰动迅速减小，进而平衡了算法的探索和开发能力。

方差和标准差：

1、正负1倍标准偏差的概率 =68.3%；

2、正负2倍标准偏差的概率 =95.5%；

3、正负3倍标准偏差的概率 =99.7%；

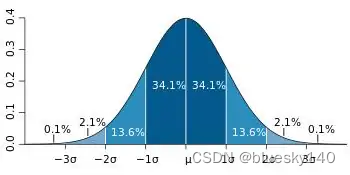
标准差（standard deviation)

标准差是一组数值自平均值分散程度的一种测量观念。

一个较大的标准差，代表大部分的数值和其平均值之间差异较大，一个较小的标准差，代表这些数值较接近平均值。

例如：

两组数的集合 {0， 5， 9， 14} 和 {5， 6， 8， 9} 其平均值都是7，但第二个集合具有较小的标准差

标准差应用于投资上，可作为量度回报稳定性的指标。标准差数值越大，代表回报远离过去平均数值，回报较不稳定故风险越高。相反，标准差数值越小，代表回报较为稳定，风险亦较小。
?

例如：

A，B两组各有6位学生参加同一次语文测验，A组的分数为95，85，75，65，55，45　　

B组的分数为73，72，71，69，68，67

?

这两组的平均数都是70，但A组的标准差为17.078分，B组的标准差为2.160分，说明A组学生之间的差距要比B组学生之间的差距大得多

上面的靶上有两套落点。尽管两套落点的平均中心位置都在原点?(即期望相同），但两套落点的离散程度明显有区别。蓝色的点离散程度更小。

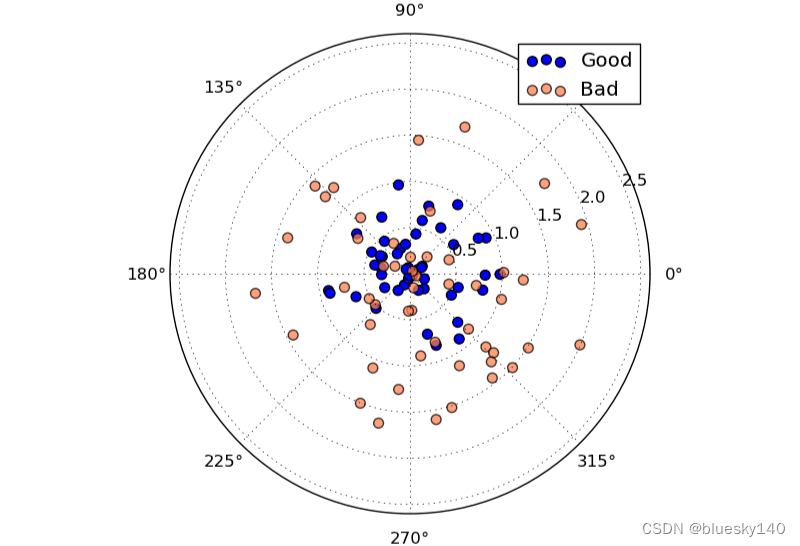
方差（variance)：

数学上，我们用方差来代表一组数据或者某个概率分布的离散程度。可见，方差是独立于期望的另一个对分布的度量。两个分布，完全可能有相同的期望，而方差不同，正如我们上面的箭靶。

标准差和方差的关系为：

搜索文章顺序：标题-主题-全文

惯性权重总是和位置联系在一起，在其它地方就叫调整因子、惯性因子、权重因子、收缩策略等。

初始化

惯性因子

位置更新1或2个。全局一个，局部一个。

E

朋友说的话：引导直播预约，钩子引导私域，不浪费每一个流量价值。

地上本没有坑，拿铲子挖出坑来。