【寒假打卡】Day01

选择

如下代码输出的是什么（ ）

char a=101;
int sum=200;
a+=27;sum+=a;
printf("%d\n",sum);

A: 32 B: 99 C: 328 D: 72

答案： C

解析： 首先，char a = 101; 定义了一个字符变量 a，并将其赋值为 101。由于 ASCII 编码中 101 对应的字符是 'e'，所以 a 的值为 'e'。

然后，a += 27; 将 a 的值增加 27。由于 a 的类型是 char，其取值范围为 -128 到 127，所以这里的加法会发生溢出。27 加上 101 的结果是 128，超过了 char 的取值范围。根据 C++ 的规定，溢出时 char 类型会进行模运算，即 128 模 256 等于 128。因此，a 的新值为 128。

接下来，sum += a; 将 sum 的值增加 a。sum 的初始值是 200，a 的新值是 128，所以 sum 的新值为 328。

最后，printf("%d\n", sum); 使用 printf 函数以十进制格式输出 sum 的值。因此，程序输出的结果是 328。

---

对于下面代码执行后输出的是什么（ ）

int value = 1024;
char condition = *((char*)(&value));
if(condition) value += 1; condition = *((char*)(&value));
if(condition) value += 1; condition = *((char*)(&value));
printf("%d %d", value, condition);
void func(char para[100])
{
void *p = malloc(100);
printf("%d, %d\n", sizeof(para), sizeof(p));
}

A: 1026 1 B: 1025 0 C: 1025 1 D: 1024 0

答案： C

解析：
先将一个整型值 1024 转换为了字符指针类型，并通过指针对内存进行访问。然后我们判断这个字符的值，如果不为0（即非零），则将整型值加上1。接着我们再次将整型值转换为字符指针类型，并通过指针对内存进行访问，判断第二个字符的值。最后输出整型值和最后一个字符的值（即条件变量的值）。由于整型值 1024 的二进制表示为 0000 0100 0000 0000，其中最低有效字节为 0，所以第一个条件不满足，整型值不变。而第二个条件满足，整型值加上了 1，并且最后一个字符的值为 1。

---

假设在32位机器上，读代码选结果（ ）

void func(char para[100])
{
void *p = malloc(100);
printf("%d, %d\n", sizeof(para), sizeof(p));
}

A: 4,4 B: 100,4 C: 4,100 D: 100,100

答案： B

解析：
在32位机器上，指针的大小通常为4字节。因此，在这种情况下，函数func的输出结果将是100, 4。

虽然在函数参数中声明了char para[100]，但实际上这里的数组参数会被调整为char* para，因此sizeof(para)返回的是指针的大小而不是数组的大小。数组作为函数参数传递时会退化为指针。

sizeof运算符在编译时求值，返回的是类型的大小，而不是运行时变量的大小。所以无论传递给func的数组实际存储了多少数据，sizeof(para)都会返回100。

---

以下程序执行后的输出结果为（ ）

#include <stdio.h>
void func(char *p) { p = p + 1; }
int main()
{
char s[] = {'1', '2', '3', '4'};
func(s);
printf("%c", *s);
return 0;
}

A: 2 B: 编译错误 C: 1 D: 无法确定

答案： C

解析：
在函数func中，参数p是一个指向字符类型的指针。在函数体内，我们将指针p的值加上1，但这个操作只是修改了指针本身的值，并不影响指针所指向的内存地址及其内容。

在主函数中，定义了一个字符数组s，并将其初始化为{'1', '2', '3', '4'}。调用函数func(s)时，将s数组的首地址传递给了函数func。函数func中对指针进行了修改，但并未修改s数组中的数据。因此，在printf语句中输出s数组的第一个元素，即输出字符1。

---

已知数组D的定义是 int D[4][8]; 现在需要把这个数组作为实参传递给一个函数进行处理。下列可以作为对应的形参变量说明的是【多选】（ ）
A: int D[4][] B: int *s[8] C: int(*s)[8] D: int D[][8]

答案： CD

---

编程

HJ99 自守数

HJ99 自守数
描述
自守数是指一个数的平方的尾数等于该数自身的自然数。例如：25^2 = 625，76^2 = 5776，9376^2 = 87909376。请求出n(包括n)以内的自守数的个数

数据范围：
1≤n≤10000

输入描述：
int型整数

输出描述：
n以内自守数的数量。

示例1
输入：
6
复制
输出：
4
复制
说明：有0，1，5，6这四个自守数
示例2
输入：
1
复制
输出：
2
复制
说明：有0, 1这两个自守数

代码：
规律：个位数为 0、1、5、6 的数才可能是自守数，故采用筛选法，只判断符合该条件的数

#include <iostream>
using namespace std;

int main() {
    int n;
    while (cin >> n) {
        int cnt = 1;
        int base = 10;
        for (int i = 1; i <= n; i++) {
            if (i % 10 == 0 || i % 10 == 1 || i % 10 == 5 || i % 10 == 6) {
                int x = i * i;
                if (i == base)
                    base *= 10;
                if (x % base == i)
                    cnt++;
            }

        }
        cout << cnt << endl;
    }

    return 0;
}

---

OR86 返回小于 N 的质数个数

OR86 返回小于 N 的质数个数

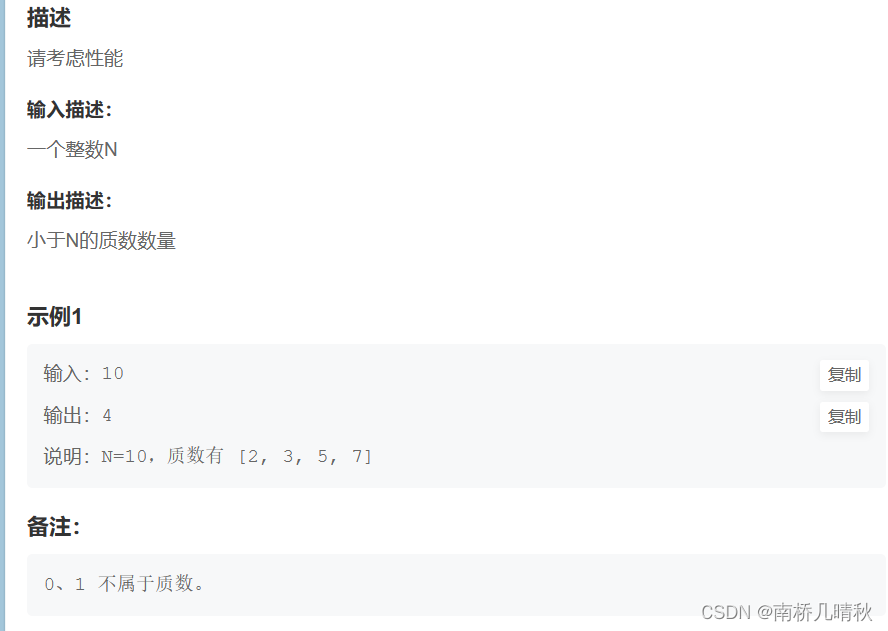
代码：

#include <iostream>
using namespace std;

bool isPrime(int n)
{
    for(int i=2;i*i<=n;i++)
    {
        if(n%i==0)
            return false;
    }
    return true;

}

int main() {
    int n;
    int cnt=0;
    cin>>n;
    for(int i=2;i<=n;i++)
    {
        if(isPrime(i))
            cnt++;
    }
    cout<<cnt<<endl;
    return 0;
}