计数排序 CountingSort
发布时间:2023年12月31日
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
动画演示 :
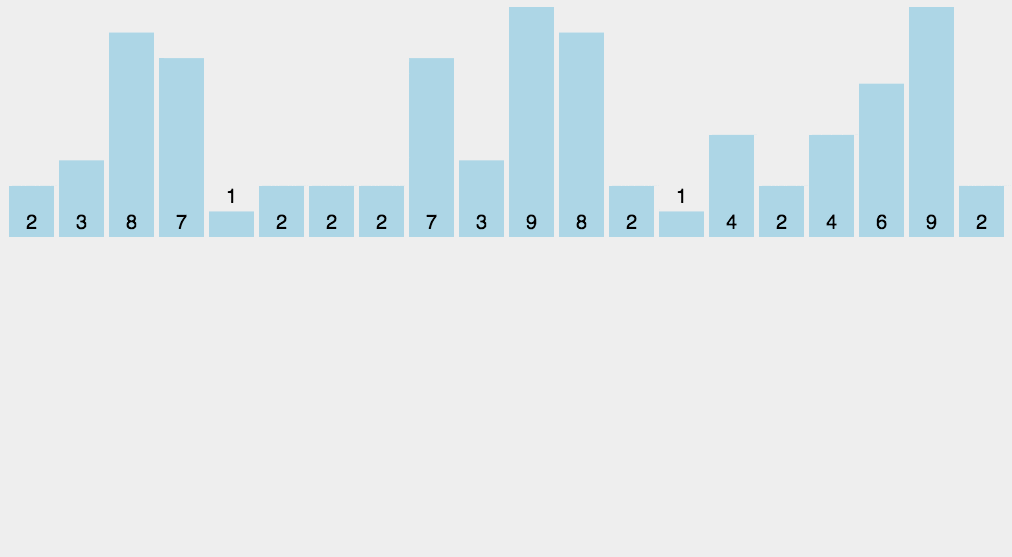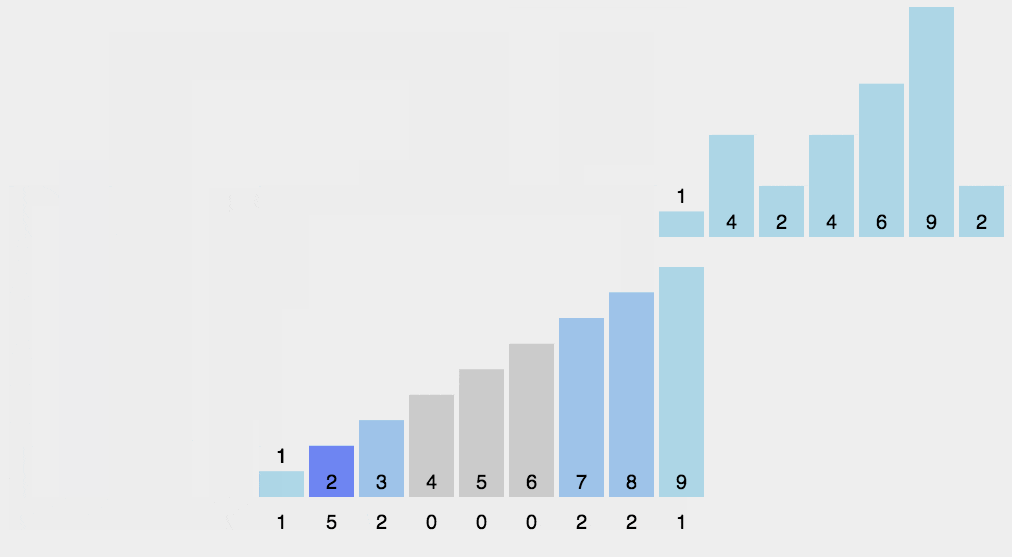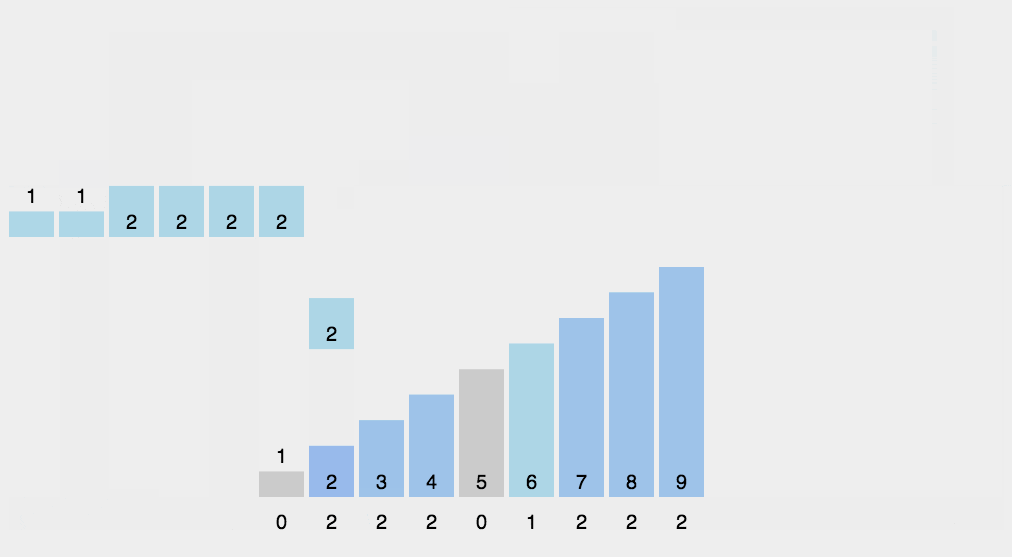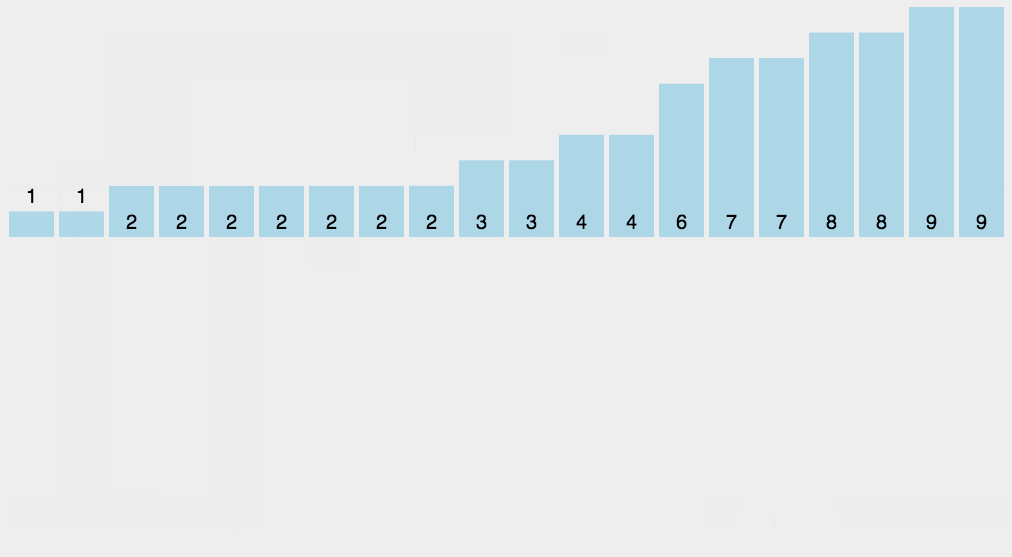
案例代码 : (此代码有些瑕疵 , 不能处理负数)
public static void main(String[] args) {
//int[] arr = {10, 78, 65, 32, 21, 89, 13, 54, 7, 3};
//sort(arr);
int[] brr = {0, 1,1, 7, 8, 9, 10};
//Tsort(brr, 3);
CountingSort(brr);
}
public static void CountingSort(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max)
max = arr[i];
}
int[] count = new int[max + 1];
for (int i = 0; i < arr.length; i++) {
count[arr[i]]++;
}
//合并
int n = 0;
for (int i = 0; i < max; i++) {
while (count[i] != 0) {
arr[n++] = i;
count[i]--;
}
}
//打印
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}?代码 :
public static void CountingSorts(int[] arr) {
int max = arr[0];
int min = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max)
max = arr[i];
else if (arr[i] < min)
min = arr[i];
}
int[] count = new int[max - min + 1];
for (int i = 0; i < arr.length; i++) {
count[arr[i] - min]++;
}
//合并
int n = 0;
for (int i = 0; i < count.length; i++) {
while (count[i] != 0) {
arr[n++] = min + i;
count[i]--;
}
}
//打印
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}这期就到这 .
文章来源:https://blog.csdn.net/sytdsqzr/article/details/135317829
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 多元高斯分布:条件分布推导
- Vite 打包时修改静态资源的路径
- Vulnhub-Al-Web-1.0 靶机复现完整过程
- 【Web前端大作业】基于HTML+CSS+JavaScript制作西北大学新闻网站(7页)
- 消费可靠性投递-confirm确认模式
- 电脑开机出现:CLIENT MAD ADDR (网卡启动系统)的解决办法
- Comdlg32.dll文件丢失怎么?Comdlg32.dll修复方法
- MyBatisX快速开发插件 [MyBatis-Plus系列]
- YOLOv7独家原创改进:一种新颖的自适应空间相关性金字塔注意力 ,实现小目标暴力涨点
- 14.10-其他阻塞和非阻塞混合使用的原则