数据结构学习 jz16 数值的整数次方
发布时间:2024年01月05日
关键词:快速幂 位运算
之前已经学过快速幂了,所以只是回忆。快速幂有递归版和非递归版。
题目:
这道题和之前的快速幂的区别是 n可能为负数。分类讨论即可。

思路:
区分正负:
if (n < 0) return POW(1.0 / x, -b);
else return POW(x, b);注意:
把n赋给long b。
因为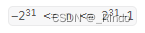
如果n=-2^31,如果取-n,就会爆,因为int装不下2^31。
long b = n;复杂度计算:
时间复杂度O(logN)
空间复杂度O(1) 非递归版
代码:
非递归版:
class Solution {
public://快速幂非递归版
double myPow(double x, int n) {
long b = n;
if (n < 0) return POW(1.0 / x, -b);
else return POW(x, b);
}
double POW(double x, long n)
{
double res = 1;
double rex = x;
while (n)
{
if (n & 1)
{
res *= rex;
}
rex *= rex;
n=n >> 1;
}
return res;
}
};递归版:
class Solution {
public://快速幂递归版
double myPow(double x, int n) {
long b=n;
if(n<0) return POW(1.0/x,-b);
else return POW(x,b);
}
double POW(double x, long n)
{
double res=0;
if(n==1) return x;
if(n==0) return 1;
if(n&1)
res=x*POW(x,n-1);
else
{
res=POW(x,n/2);
res=res*res;
}
return res;
}
};
文章来源:https://blog.csdn.net/rainssssss/article/details/135415245
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!