神经网络：卷积层知识点

1.卷积有什么特点

卷积主要有三大特点：

1. 局部连接。比起全连接，局部连接会大大减少网络的参数。在二维图像中，局部像素的关联性很强，设计局部连接保证了卷积网络对图像局部特征的强响应能力。

2. 权值共享。参数共享也能减少整体参数量，增强了网络训练的效率。一个卷积核的参数权重被整张图片共享，不会因为图像内位置的不同而改变卷积核内的参数权重。

3. 下采样。下采样能逐渐降低图像分辨率，实现了数据的降维，并使浅层的局部特征组合成为深层的特征。下采样还能使计算资源耗费变少，加速模型训练，也能有效控制过拟合。

2.不同层次的卷积都提取什么类型的特征

1. 浅层卷积 $\to$ 提取边缘特征

2. 中层卷积 $\to$ 提取局部特征

3. 深层卷积 $\to$ 提取全局特征

3.卷积核大小如何选取

最常用的是 $3\times 3$ 大小的卷积核，两个 $3\times 3$ 卷积核和一个 $5\times 5$ 卷积核的感受野相同，但是减少了参数量和计算量，加快了模型训练。与此同时由于卷积核的增加，模型的非线性表达能力大大增强。

不过大卷积核（ $7\times 7，9\times 9$ ）也有使用的空间，在GAN，图像超分辨率，图像融合等领域依然有较多的应用，大家可按需切入感兴趣的领域查看相关论文。

4.卷积感受野的相关概念

目标检测和目标跟踪很多模型都会用到RPN层，anchor是RPN层的基础，而感受野（receptive field，RF）是anchor的基础。

感受野的作用：

1. 一般来说感受野越大越好，比如分类任务中最后卷积层的感受野要大于输入图像。

2. 感受野足够大时，被忽略的信息就较少。

3. 目标检测任务中设置anchor要对齐感受野，anchor太大或者偏离感受野会对性能产生一定的影响。

感受野计算：

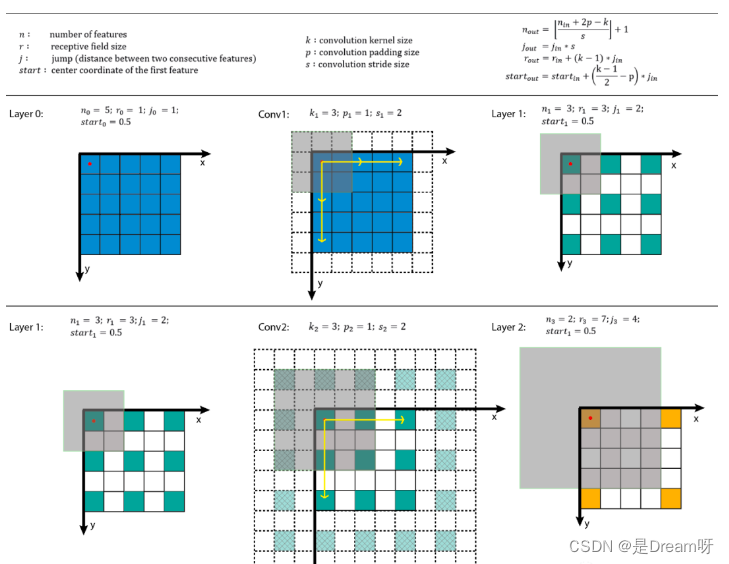
增大感受野的方法：

1. 使用空洞卷积

2. 使用池化层

3. 增大卷积核

5.网络每一层是否只能用一种尺寸的卷积核

常规的神经网络一般每层仅用一个尺寸的卷积核，但同一层的特征图可以分别使用多个不同尺寸的卷积核，以获得不同尺度的特征，再把这些特征结合起来，得到的特征往往比使用单一尺寸卷积核的要好，如GoogLeNet 、Inception系列的网络，均是每层使用了多个不同的卷积核结构。如下图所示，输入的特征图在同一层分别经过
$1\times 1$ ， $3\times 3$ 和 $5\times 5$ 三种不同尺寸的卷积核，再将各自的特征图进行整合，得到的新特征可以看作不同感受野提取的特征组合，相比于单一尺寸卷积核会有更强的表达能力。

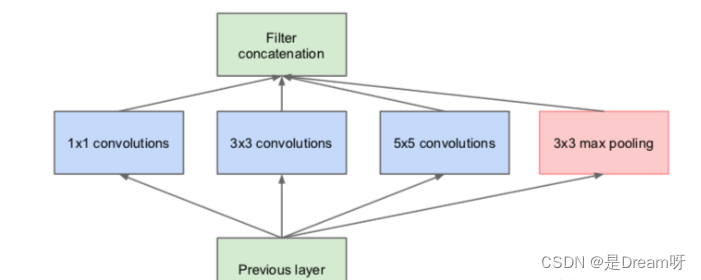
6.1*1卷积的作用

$1?1$ 卷积的作用主要有以下几点：

1. 实现特征信息的交互与整合。

2. 对特征图通道数进行升维和降维，降维时可以减少参数量。

3. $1?1$ 卷积+ 激活函数 $\to$ 增加非线性，提升网络表达能力。

$1?1$ 卷积首发于NIN（Network in Network），后续也在GoogLeNet和ResNet等网络中使用。感兴趣的朋友可追踪这些论文研读细节。

7.转置卷积的作用

转置卷积通过训练过程学习到最优的上采样方式，来代替传统的插值上采样方法，以提升图像分割，图像融合，GAN等特定任务的性能。

转置卷积并不是卷积的反向操作，从信息论的角度看，卷积运算是不可逆的。转置卷积可以将输出的特征图尺寸恢复卷积前的特征图尺寸，但不恢复原始数值。

转置卷积的计算公式：

我们设卷积核尺寸为 $K\times K$ ，输入特征图为 $i\times i$ 。

（1）当 $stride=1，padding=0$ 时：

输入特征图在进行转置卷积操作时相当于进行了 $padding=K?1$ 的填充，接着再进行正常卷积转置之后的标准卷积运算。

输出特征图的尺寸 = $i+(K?1)$

（2）当 $stride>1，padding=0$ 时：

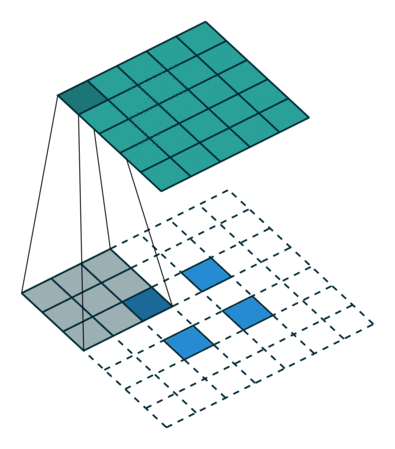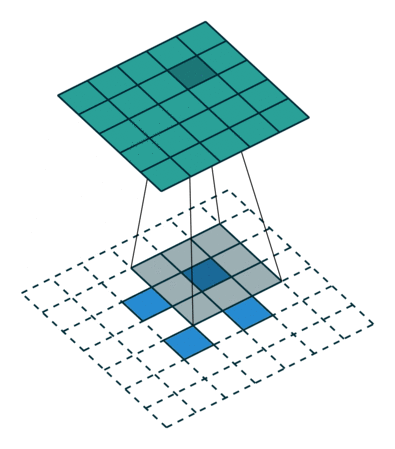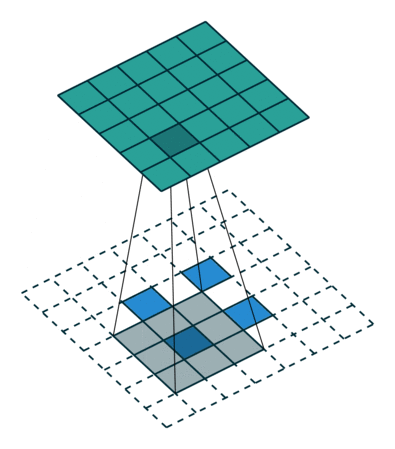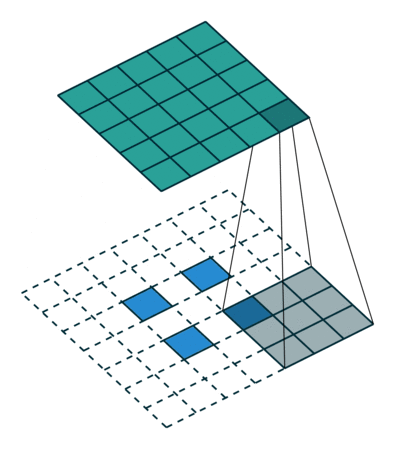
输入特征图在进行转置卷积操作时相当于进行了 $padding=K?1$ 的填充，相邻元素间的空洞大小为 $stride?1$ ，接着再进行正常卷积转置之后的标准卷积运算。

输出特征图的尺寸 = $stride?(i?1)+K$

8.空洞卷积的作用

空洞卷积的作用是在不进行池化操作损失信息的情况下，增大感受野，让每个卷积输出都包含较大范围的信息。

空洞卷积有一个参数可以设置dilation rate，其在卷积核中填充dilation rate个0，因此，当设置不同dilation rate时，感受野就会不一样，也获取了多尺度信息。

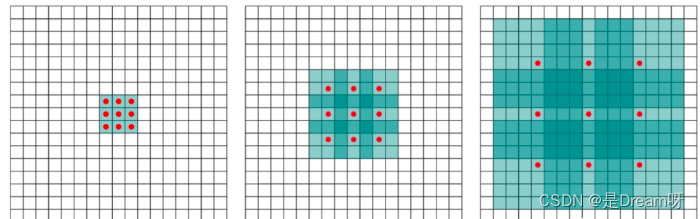
(a) 图对应 $3\times 3$ 的1-dilated conv，和普通的卷积操作一样。(b)图对应 $3\times 3$ 的2-dilated conv，实际的卷积kernel size还是 $3\times 3$ ，但是空洞为 $1$ ，也就是对于一个 $7\times 7$ 的图像patch，只有$9$个红色的点和 $3\times 3$ 的kernel发生卷积操作，其余的点的权重为 $0$ 。?图是4-dilated conv操作。

9.什么是转置卷积的棋盘效应

造成棋盘效应的原因是转置卷积的不均匀重叠（uneven overlap）。这种重叠会造成图像中某个部位的颜色比其他部位更深。

在下图展示了棋盘效应的形成过程，深色部分代表了不均匀重叠：

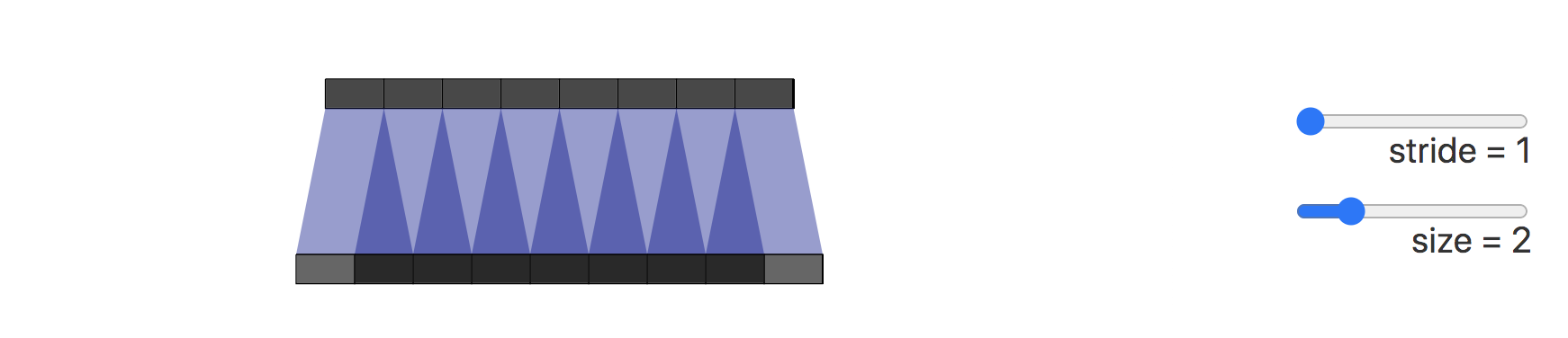
接下来我们将卷积步长改为2，可以看到输出图像上的所有像素从输入图像中接收到同样多的信息，它们都从输入图像中接收到一个像素的信息，这样就不存在转置卷带来的重叠区域。

我们也可以直接进行插值Resize操作，然后再进行卷积操作来消除棋盘效应。这种方式在超分辨率重建场景中比较常见。例如使用双线性插值和近邻插值等方法来进行上采样。

10.什么是有效感受野

感受野的相关知识在上面的第四节中中介绍过。

我们接着再看看有效感受野(effective receptive field, ERF)的相关知识。

一般而言，feature map上有效感受野要小于实际感受野。其有效性，以中心点为基准，类似高斯分布向边缘递减。

总的来说，感受野主要描述feature map中的最大信息量，有效感受野则主要描述信息的有效性。

11.分组卷积的相关知识

分组卷积（Group Convolution）最早出现在AlexNet网络中，分组卷积被用来切分网络，使其能在多个GPU上并行运行。

普通卷积进行运算的时候，如果输入feature map尺寸是 $C\times H\times W$ ，卷积核有N个，那么输出的feature map与卷积核的数量相同也是N个，每个卷积核的尺寸为 $C\times K\times K$ ，N个卷积核的总参数量为 $N\times C\times K\times K$ 。

分组卷积的主要对输入的feature map进行分组，然后每组分别进行卷积。如果输入feature map尺寸是 $C\times H\times W$ ，输出feature map的数量为 $N$ 个，如果我们设定要分成G个group，则每组的输入feature map数量为 $\frac{C}{G}$ ，则每组的输出feature map数量为 $\frac{N}{G}$ ，每个卷积核的尺寸为 $\frac{C}{G}\times K\times K$ ，卷积核的总数仍为N个，每组的卷积核数量为 $\frac{N}{G}$ ，卷积核只与其同组的输入map进行卷积，卷积核的总参数量为 $N\times \frac{C}{G}\times K\times K$ ，易得总的参数量减少为原来的 $\frac{1}{G}$ 。

分组卷积的作用:

1. 分组卷积可以减少参数量。
2. 分组卷积可以看成是稀疏操作，有时可以在较少参数量的情况下获得更好的效果（相当于正则化操作）。
3. 当分组数量等于输入feature map通道数量，输出feature map数量也等于输入feature map数量时，分组卷积就成了Depthwise卷积，可以使参数量进一步缩减。