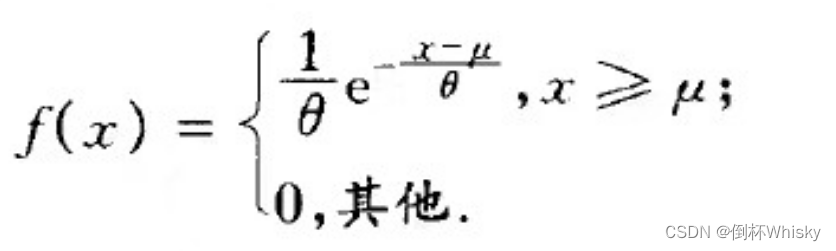参数学习——糖果问题（人工智能期末复习）

之前看了好久都不知道这题咋写，后来看了这篇机器智能-高频问题：糖果问题，大概看明白了，其实主要围绕着这两个公式

结合两道题分析

己知有草莓味和酸橙味两种类型的糖果，分别放入5种不同的包装之中，
h1包装中100%是草莓味
h2包装中75%是草莓味25%是酸橙味
h3包装中50%是草莓味50%是酸橙味
h4包装中25%是草莓味75%是酸橙味
h5包装中100%是酸橙味
假定h1,h2… h5的先验分布概率为<0.1,0.2,0.4,0.2,0.1>，每次拿出糖果是相互独立的且不影响袋子里面糖果的比例，试回答下列问题：
(1)假定拿出的2个糖果都是草莓味，请分别计算每拿出一个糖果后h1到h5的概率值；
(2)在(1)的基础上计算下个糖果为草莓味，酸橙味的概率；
(3)设x₁,x₂…x_N是取自总样本X的一个观察序列，满足如下的分布

θ>0，求θ，μ的极大似然估计。

解：
(1)

• 拿出的第一个是草莓味
  分别计算拿出的第一个是草莓味(d)的前提下从hi包装拿出的概率
  P(h1|d) = 0.1×1×a=0.1a
  P(h2|d) = 0.2×0.75×a=0.15a
  P(h3|d) = 0.4×0.5×a=0.2a
  P(h4|d) = 0.2×0.25×a=0.05a
  P(h5|d) = 0.1×0×a=0
  进行归一化：0.1a+0.15a+0.2a+0.05a+0=1 → a=2
  因此
  P(h1|d) = 0.1×1×a=0.2
  P(h2|d) = 0.2×0.75×a=0.3
  P(h3|d) = 0.4×0.5×a=0.4
  P(h4|d) = 0.2×0.25×a=0.1
  P(h5|d) = 0.1×0×a=0
• 拿出的第二个还是草莓味
  P(h1|d) = 0.1×1×1×a=0.1a
  P(h2|d) = 0.2×0.75×0.75×a=0.1125a
  P(h3|d) = 0.4×0.5×0.5×a=0.1a
  P(h4|d) = 0.2×0.25×0.25×a=0.0125a
  P(h5|d) = 0.1×0×0×a=0
  进行归一化：0.1a+0.1125a+0.1a+0.0125a+0=1 → a=40/13
  所以
  P(h1|d) = 0.1×1×1×a=0.3
  P(h2|d) = 0.2×0.75×0.75×a=0.346
  P(h3|d) = 0.4×0.5×0.5×a=0.3
  P(h4|d) = 0.2×0.25×0.25×a=0.038
  P(h5|d) = 0.1×0×0×a=0

(2)
在第一题的基础上我们已经计算出了拿的包装是hi的概率，这一问就利用P(hi|d)来预测下一个糖的概率
在已知拿出了前两个都是草莓味(d)的前提下，预测下一个糖是草莓味(X)的概率
P(X|d) = ∑P(X|hi)P(hi|d) = 1×0.3+0.75×0.346+0.5×0.3+0.25×0.038+0 = 0.719

在已知拿出了前两个都是草莓味(d)的前提下，预测下一个糖是酸橙味(Y)的概率
P(Y|d) = ∑P(Y|hi)P(hi|d) = 0+0.25×0.346+0.5×0.3+0.75×0.038+0 = 0.265

(3)
其实这一问和这整题都没太大关系，直接用概率论(/高数)的知识做就好了
首先先求似然函数

L(μ,θ) = ${\prod }_{i=1}^n$f(x) = ${\prod }_{i=1}^n$ $\frac{1}{\theta }$ $e^{?\frac{x_i?\mu }{\theta }}$

然后取对数

lnL = ${\sum }_{i=1}^n$ (-lnθ- $\frac{x_i?\mu }{\theta }$) = -nlnθ- $\frac{1}{\theta }$[ ${\sum }_{i=1}^n$ $x_i$ - nμ]

分别对μ和θ求偏导

$\frac{?lnL}{?\mu }$ = $\frac{\theta }{n}$
$\frac{?lnL}{?\theta }$ = - $\frac{\theta }{n}$+ $\frac{1}{{\theta }^2}$[ ${\sum }_{i=1}^n$ $x_i$ - nμ]

$\frac{\theta }{n}$>0，因此当μ = min{x₁,x₂…x_N}时，lnL取最大值；

令-$\frac{\theta }{n}$+$\frac{1}{{\theta }^2}$[${\sum }_{i=1}^n$$x_i$ - nμ] = 0，解得θ = $\frac{1}{n}$${\sum }_{i=1}^n$$x_i$ - μ = $\bar{X}$-μ

所以μ和θ的最大似然估计量分别为： $\hat{\mu }$ = min{x₁,x₂…x_N}，$\hat{\theta }$ = $\bar{X}$ - min{x₁,x₂…x_N}

---

已知有5种包含的糖果：
h1：草莓味100%
h2：草莓味80%、酸橙味20%
h3：草莓味50%、酸橙味50%
h4：草莓味20%、酸橙80%
h5：酸橙味100%
5种包装的先验概率分别是10%、20%、30%、10%、30%
假定依次从袋子里拿出3个糖果分别是草莓味、酸橙味、酸橙味包装内的糖果数量是无穷多的，回答下列问题
1)分别计算该袋子为h1到h5的概率；
2)下一个糖果是草莓味和酸橙味的概率；
3)如果包装里面的糖果数量有限，分析比较一下拿出的3个糖果按顺序分别是草莓味、酸橙味、酸橙味以及酸橙味、草莓味、酸橙味对h1到h5概率的大小影响。

解：
(1)

• 拿出的第一个是草莓味
  P(h1|d) = 0.1×1×a=0.1a
  P(h2|d) = 0.2×0.8×a=0.16a
  P(h3|d) = 0.3×0.5×a=0.15a
  P(h4|d) = 0.1×0.2×a=0.02a
  P(h5|d) = 0.3×0×a=0
  进行归一化：0.1a+0.16a+0.15a+0.02a+0=1 → a=100/43
  因此
  P(h1|d) = 0.1×1×a=0.23
  P(h2|d) = 0.2×0.8×a=0.37
  P(h3|d) = 0.3×0.5×a=0.35
  P(h4|d) = 0.1×0.2×a=0.05
  P(h5|d) = 0.3×0×a=0
• 拿出的第二个是酸橙味
  P(h1|d) = 0.1×1×0×a=0
  P(h2|d) = 0.2×0.8×0.2×a=0.032a
  P(h3|d) = 0.3×0.5×0.5×a=0.075a
  P(h4|d) = 0.1×0.2×0.8×a=0.016a
  P(h5|d) = 0.3×0×1×a=0
  进行归一化：0+0.032a+0.075a+0.016a+0=1 → a=1000/123
  所以
  P(h1|d) = 0.1×1×0×a=0
  P(h2|d) = 0.2×0.8×0.2×a=0.26
  P(h3|d) = 0.3×0.5×0.5×a=0.61
  P(h4|d) = 0.1×0.2×0.8×a=0.13
  P(h5|d) = 0.3×0×1×a=0
• 拿出的第三个还是酸橙味
  P(h1|d) = 0.1×1×0×0×a=0
  P(h2|d) = 0.2×0.8×0.2×0.2×a=0.0064a
  P(h3|d) = 0.3×0.5×0.5×0.5×a=0.0375a
  P(h4|d) = 0.1×0.2×0.8×0.8×a=0.0128a
  P(h5|d) = 0.3×0×1×1×a=0
  进行归一化：0+0.0064a+0.0375a+0.0128a+0=1 → a=10000/567
  所以
  P(h1|d) = 0.1×1×0×0×a=0
  P(h2|d) = 0.2×0.8×0.2×0.2×a=0.11
  P(h3|d) = 0.3×0.5×0.5×0.5×a=0.66
  P(h4|d) = 0.1×0.2×0.8×0.8×a=0.23
  P(h5|d) = 0.3×0×1×1×a=0

(2)

下一个糖是草莓味(X)的概率
P(X|d) = ∑P(X|hi)P(hi|d) = 0.8×0.11+0.5×0.66+0.2×0.23 = 0.46

下一个糖是酸橙味(Y)的概率
P(Y|d) = ∑P(Y|hi)P(hi|d) = 0.2×0.11+0.5×0.66+0.8×0.23 = 0.53

(3)包装里面的糖果数量是有限的还是无限的实际上都是一样的，还是回到概率论的问题，因此h1到h5的概率都不变。