Codeforces Round 915 (Div. 2)

Constructive Problems（Problem - A - Codeforces）

题目大意：现在有一片城市被摧毁了，需要进行重建，当一个城市水平相邻和竖直相邻的位置都至少有一个城市的时候，该城市可以被重建。所有城市排成n行m列的矩形，政府先拨款重建一部分城市，剩下的需要各个城市自建，问政府最少需要重建多少个城市。

思路：我们可以发现，要想重建，城市需要是锯齿形的，即：

如上图，我们可以发现，同样是4个，但是左图中四个可以伸延至整个区间，右图中则一个也不能往外延伸了，所以，我们可以发现，这样斜着的是最优解。那么对于矩形的，如下图

所以很容易发现斜着只能补成一个正方形，要使整个区域都被覆盖到，那么就要取最长的那条边的长度作为个数。

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n,m;
		scanf("%d%d",&n,&m);
		int ans=max(n,m);
		printf("%d\n",ans);
	}
}

?Begginer's Zelda（Problem - B - Codeforces）

题目大意：给定一棵树，我们每次操作可以选择树上的两个点，然后将两点及中间的路径合并成一个点。问要将整棵树合并成一个点，最少需要操作多少次。

思路：这道题怎么说呢，挺难受的。我最开始分析样例，因为样例给的数据都很简单，所以抽出最长路然后剩下的都是直接连在最长路上的点，稍微讨论一下就行，但是显然，这是有bug的，

比如上图，抽出最长路后，剩下的点不是直接连在最长路上的。所以很明显，最长路这个思路是不通的，然后，我竟然又想到每合并一次就去找最长路，说人话就是去直接模拟我认为的最优策略。这样的话有两个问题，一个是最长路上的各点其实没有那么容易确定，我们能确定的就是起点、终点以及路径长度，所以合并操作实际并不容易。另外一个是，这个会出现超时问题，因为我们要找很多次。所以此路不通。然后我又想到能不能从出度的角度来考虑，然后我想到的是从出度最大的那些点入手去找规律，显然越讨论越复杂，它们根本不具有什么规律。至此我想到的路全部不通，而且推理验证实际上花的时间远比把这几行思路敲出来要多。最后这道题的思路实际上是从出度最少的点入手，我们仔细想想，我们的路径当延伸到一个出度大于1的点之后，肯定还能再往后延伸，直到延伸到一个出度为1的点才停。而且这个是通用的，不管我们在什么情况下，最优的路径一定要尽可能长，未必非要是最长路，但它至少是一定不能再延伸了的路。然后将这条路上的点合并成一个之后，这两个出度为1的点就消失了。那么实际上，我们只需要找到哪些点出度为1，然后两两组合，如果是奇数个，再把不能被组合的那个点加上即可。

#include<bits/stdc++.h>
using namespace std;
int d[100010];
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n;
		scanf("%d",&n);
		for(int i=1;i<=n;i++) d[i]=0;
		for(int i=1;i<n;i++)
		{
			int a,b;
			scanf("%d%d",&a,&b);
			d[a]++,d[b]++;
		}
		int cnt=0;
		for(int i=1;i<=n;i++) 
			if(d[i]==1) cnt++;
		int ans=ceil(cnt*1.0/2);
		printf("%d\n",ans);
	}
}

Largest Subsequence（Problem - C - Codeforces）

题目大意：给定一个长为n的字符串s，我们能进行的操作就是选定s中字典序最大的子序列，然后执行一次向右循环移动一位的操作。问最终能否将s变成非降序排列，如果可以输出需要进行的操作次数，如果不可以那么就输出-1.

思路：我们可以发现，对于每个字符串字典序最大的子序列有且仅有一个，而且这个序列中的字母是非递增关系。我们对s能进行的更改，其实也就是将这个子序列逆转，其他的都是改不了的。再进一步，将子序列逆转实际上，有点类似对称操作，因为子序列中第一个字母是最大的，最后要将它转到最后一位，后面的转到前面来了就不变了，所以实际上类似一个对称操作。

所以我们可以在统计最大序列的时候，将它们的下标也记录下来，然后直接在字符串里进行更改，最后判断字符串是否符合要求即可。但是对于第一个字母有多个的情况，输出操作数的时候实际是要处理一下的。因为我们正常的就是子序列长度-1，但是如下图：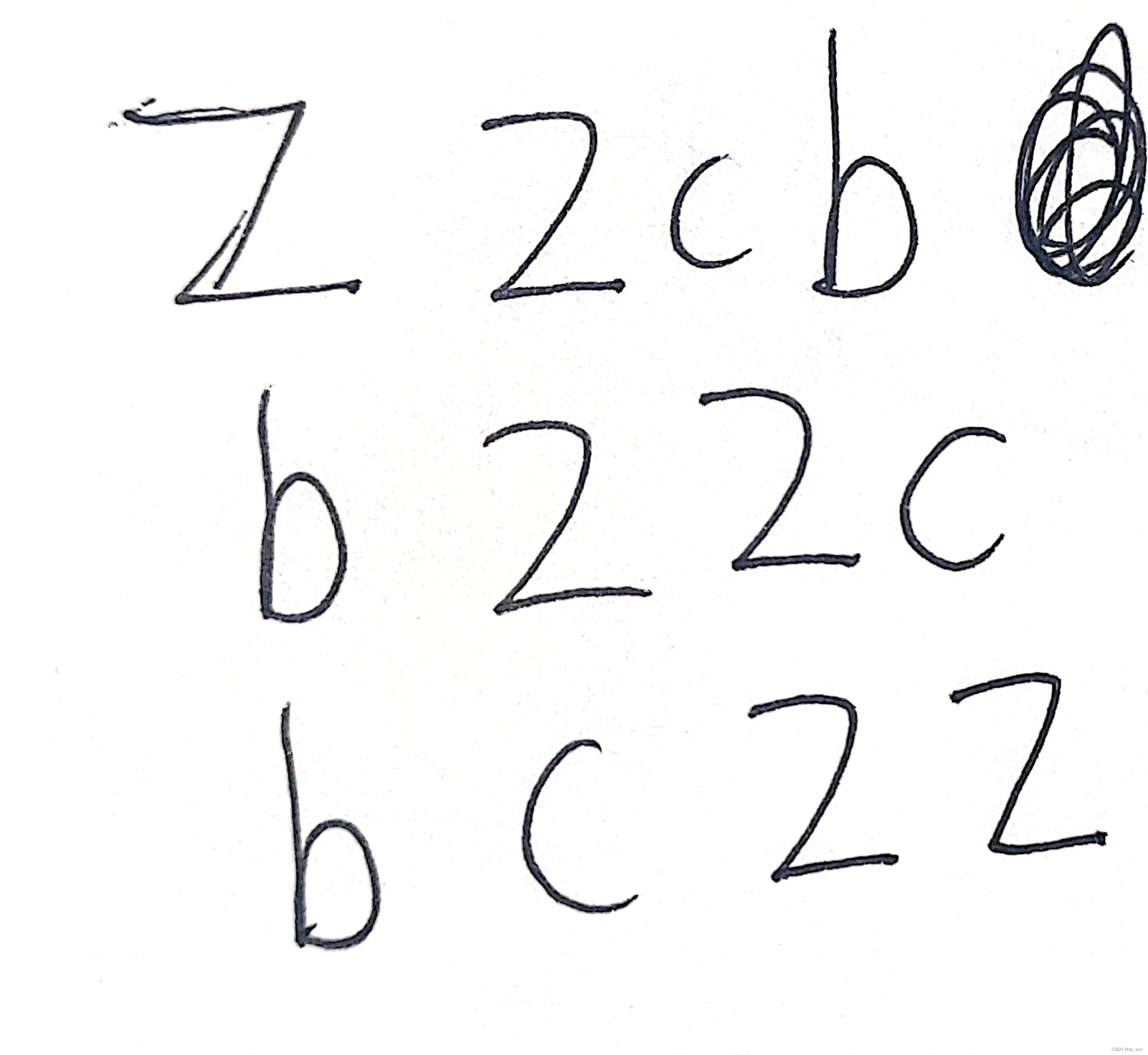

我们实际不用转那么多次。所以这个也需要特别统计一下，最后的结果应该是：子序列长度-1-（子序列首字母个数-1），对了，再多提一句，子序列是用类似于栈的思想来统计的。

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n;
		scanf("%d",&n);
		string s;
		cin>>s;
		vector<char>s1;
		vector<int>v;
		for(int i=0;i<n;i++)
		{
			while(s1.size()&&s1.back()<s[i])
			{
				v.pop_back();
				s1.pop_back();
			}
			if(!s1.size()||s1.back()>=s[i]) s1.push_back(s[i]),v.push_back(i);
		}
		int len=v.size();
		char st=s[v[0]];
		map<char,int>mp;
		for(int i=0;i<len;i++) mp[s[v[i]]]++;
		for(int i=0;i<len/2;i++)
		{
			int l=v[i],r=v[len-1-i];
			if(s[l]!=s[r])swap(s[l],s[r]);
		}
		char c=s[0];
		int flag=1;
		for(int i=1;i<s.size();i++)
		{
			if(c>s[i]) 
			{
				flag=0;
				break;
			}
			c=s[i];
		}
		if(flag) 
		{
			int ans=v.size()-1-(mp[st]-1);
			printf("%d\n",ans);
		}
		else printf("-1\n");
	}
}

ps:其实很多时候，思路无非就两种，一种是模板，就是前人把经验总结好，你学会了他们总结的经验，看到题目直接写，另外一种就是你需要自己去题目中抽丝剥茧发现规律。我们对于第一种实际上都不会多想而且我们也更喜欢第一种，因为我们知道它的正确性，把它作为一种客观真理来用，就像人有两只手，我们不会一直去追问为什么人有两只手，就这些都是自然而然地事情，这样就减少了思考的痛苦，我们只要知道即可。但是面对第二种，我们对于陌生的思路就很喜欢找到一个自然而然的知识与它绑在一起，仿佛这样就可以说服自己，没写出这道题仅仅是因为这个知识点不知道而已。但是，不是所有的题目都是水到渠成的存在，对于第二种题目我们实际上很难找到那种和它完全符合的，水到渠成的知识点，因为模板题是有限的。所以我们永远不能用更多的学习去代替思考，不是所有的题都对应一个模板。我们需要做的是抽丝剥茧，一层层分析，去分析题目本质，去分析操作的实际意义，一边分析一边去想可能的思路，正着想到的思路不通倒着能不能用，区间分析不通单点能不能分析明白，最大值没办法入手最小值能不能写出来，不断思考不断推翻不断追问，很难受但是只有这样才能获得真正的令人安心的成长。题目要么就是把本质分析清楚，要么就抽象出一个规律。就像b题，本质就是每次选的路一定要延伸到不能延伸，只有叶子节点相连才能实现，规律就是叶子节点的个数除于2上取整。当然这两种方法都逃不过分析和思考，尽管再难都要去进行大量的分析和思考，思考是无可替代的。大量题目的练习不仅是查漏补缺，去学自己不会的知识点，更多的是要强迫自己不断去思考，锻炼思考的能力。毫无头绪也罢，痛苦难受也罢，一定不要放弃思考。

这条路上你的伙伴目标可以有很多，但是对手只有你自己。所以先把目光放在自己身上，就像那个dfs的迷宫，不断地试错总会找到正确的路，而且从某种程度上来说，你已经找到了不是吗。

??

?