专题一_双指针(一)

发布时间：2024年01月03日

文章目录

283.移动零

题目链接

题目解析

在这里插入图片描述
在这里插入图片描述
题目还是比较简单的.我们通过一个实例来看一下.
在这里插入图片描述
在这里插入图片描述

讲解算法原理

这道题,也就是移动零这道题可以归类到一类题里面.
这类题可以叫做数组划分,也可以叫做数组分块.

这类题的特点就是给了我们一个数组,横线表示数组,
然后制定一个规则,让我们在这个规则下划分为若干个区间的特点

在这里插入图片描述

在这道移动零的题目里面,给了我们一个数组,然后给了我们一个标准,
你要把所有的非零元素移动到左边,所有零元素移动到右边.
因此这个数组在这个标准之下分成两个区间
在这里插入图片描述

像这类题都可以划分为数组划分或者数组分块

解决这道题我们有一个非常经典的算法,就是双指针算法.
利用数组下标来充当指针

接下来就是看我们如何用双指针算法来解决数组分块这道题.

我们先画一个数组,然后写两个指针.
注意这两个指针扫描过程中处于的位置,不是一开始的位置.
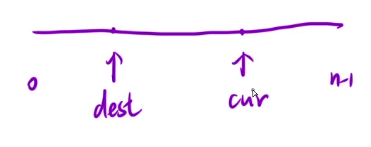
在这里插入图片描述
在这里插入图片描述

我们先不看dest,先看cur
cur从左往右扫描的时候会分为两个部分,左边这个部分,右边这个部分

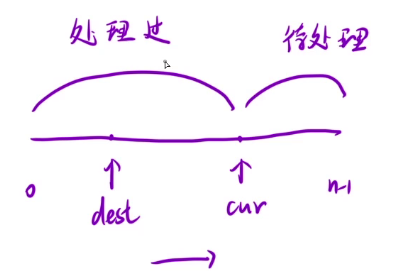
在这里插入图片描述

具体怎么处理我们先不管, 我们就认为它是处理过的区间
我们先来搞懂双指针算法的本质

处理过的区间我们想让它达到什么样目的?
就跟我们题目要求的一样,左边是为非0元素,右边是0元素
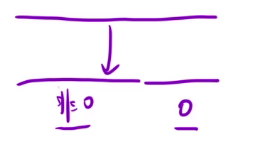
在这里插入图片描述

dest的作用其实就是一个分割线的作用,相当于左边被处理过又细化为两个小区间
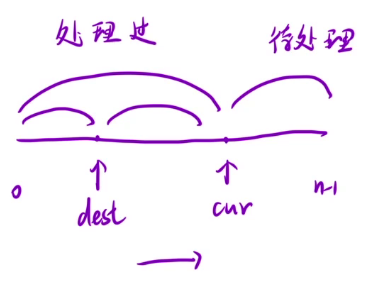
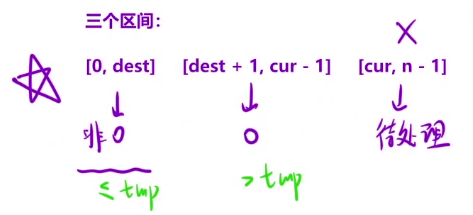
在这里插入图片描述

因此整个数组分为三个区间:
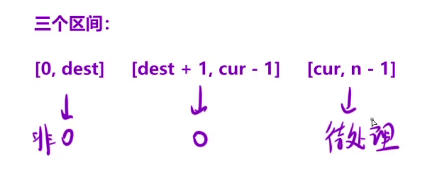
在这里插入图片描述
如果我们能够保证dest指针和cur指针, 在从左向右移动的过程中, 一直都能
让这三个区间保持这样的性质的话,
当cur指针移动到n位置的时候, 我们这个数组就划分成了
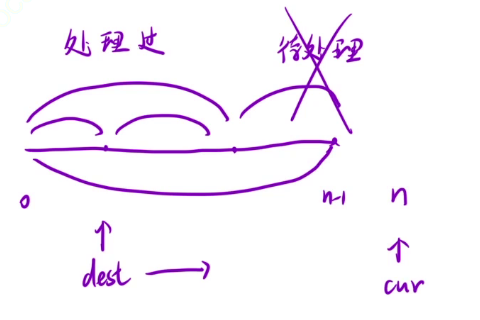
在这里插入图片描述

为什么划分成?我们看这三个区间的性质就可以了.
当cur到n的时候, 待处理的区间就不见了.
那0到n区间就被dest这个指针划分为两个部分
其中左边部分是非0元素,右边部分是0元素,这就符合题目要求了
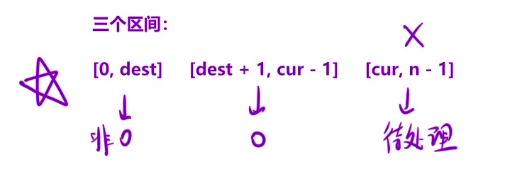
在这里插入图片描述

因此我们在接下来要做的就是,当这两个指针在从左向右的移动过程中,
一直让这三个区间保持这样的性质就可以了
这个其实就是我们双指针算法的本质,这两个指针有这个作用,这三个区间有这个性质,
我们就可以完成划分

那接下来就是如何划分了
如何划分还是比较简单的,我们通过这个实例来给大家模拟一下.

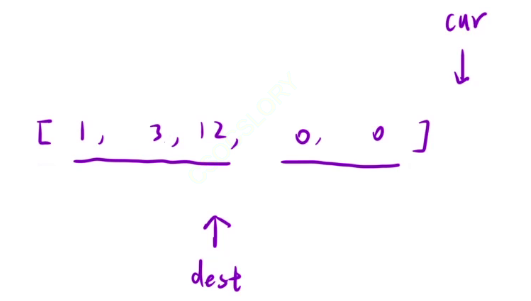
cur刚开始指向0这个位置,
因为dest的作用是已处理的区间内,非零元素的最后一个位置
刚开始扫描的时候没有非0元素,因此我们可以把dest指向-1这个位置
(刚开始还没有非0元素, 非零元素不存在代表这个区间不存在)
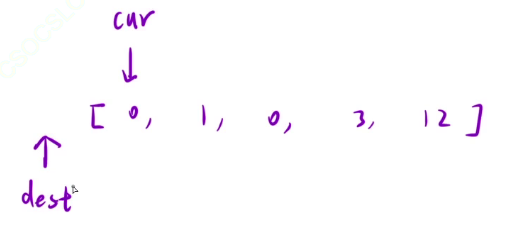
在这里插入图片描述

接下来这两个指针往右移动
dest先别动,cur先移动

cur在从左往右的过程中会遇到两种情况
第一种,遇到一个0元素
第二种,遇到一个非0元素

当cur遇到0元素的时候,我们要保证这三个区间的性质,
我们仅需要要让cur这个指针向右移动一位即可.
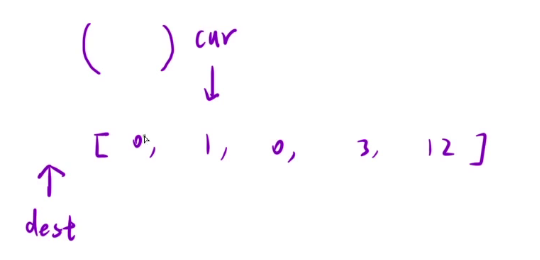
在这里插入图片描述

当cur遇到0元素的时候，我们要让这个元素加入到最左边的区间里。
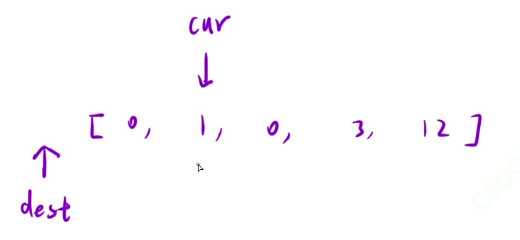
在这里插入图片描述
想加入最左边，那就相当于多了一个元素，所以dest要往后移动一位。
dest往后移动一位，1要加入到这个区间，不能直接覆盖到区间。
所以我们先让dest++，然后交换这两个位置的元素，也就是0和1。

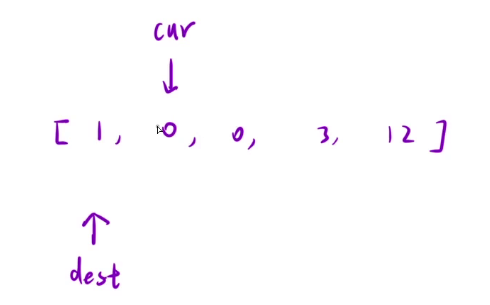
在这里插入图片描述
交换完之后，说明cur指向的元素已经处理完了，cur+1;
我们再来看这三个区间。

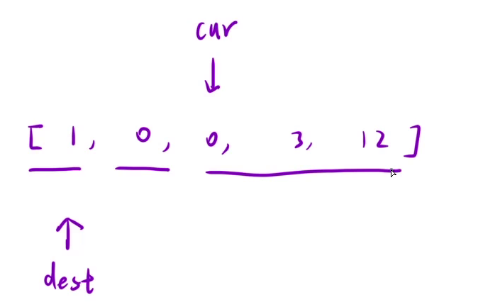
在这里插入图片描述

接下来又回到最开始，我们依次循环，一直到cur到n这个位置
我们就完成了区间的划分。

在这里插入图片描述

我们总结一下：
在这里插入图片描述

扩展

我们说一下跟这道题相关的知识点，快排
我们双指针的思想其实快排这个算法里最核心的一步，数组划分。

我们先回忆一下快排的过程，先给你一个数组，然后选一个基准元素tmp，
然后根据这个基准元素划分两个部分，其中左边这个部分全部小于tmp，
右边这个部分全部大于tmp。
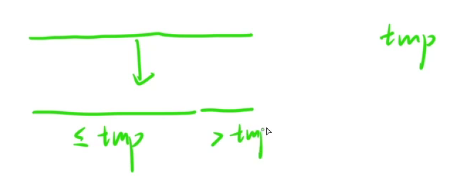
在这里插入图片描述

然后跟我们前面讲的一模一样，只要把非0改为小于tmp， 0改为大于tmp.
你会发现这道题就是快排最核心的一步，数组划分那一步。
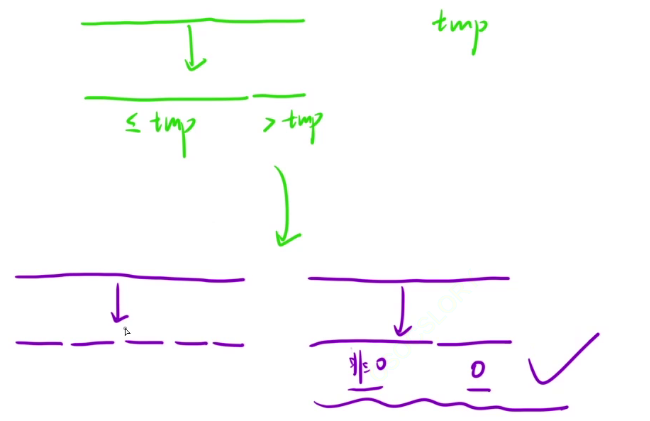
在这里插入图片描述

我们可以用双指针算法来解决快排最核心的一步：
两个指针的作用不变, 仅需修改三个区间里对应的信息就可以了
在这里插入图片描述
后面的操作 一摸一样。

我们这里给大家买一个关子，我们这个数据划分仅仅是把数组分成了两块，
它虽然能够解决快排问题，但是遇到数据量非常恶心的时候，
如果数据都是相同的时候，它的时间复杂度是接近O(N^2).

因此快排是不能处理那些比较恶心的数据的。
但是后面我们会学到颜色划分那道题，我们是把数组分成三块啊，数组分成三块。然后用那一个算法思想来解诀快排是最优秀的一个解法。

编写代码

我希望大家先根据这个算法原理，尝试一下编写代码，然后把你写的代码和我写的代码比较，
起到一个查漏补缺的作用。

首先我们在模拟算法的过程中，已经做了，初始化的时候cur=0, dest= -1;
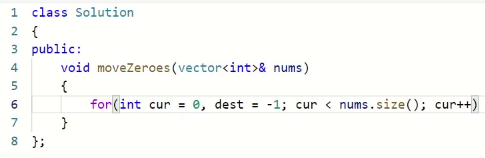
在这里插入图片描述

接下来我们判断的时候，我们是按两种情况来处理。
我们前面讲过了。
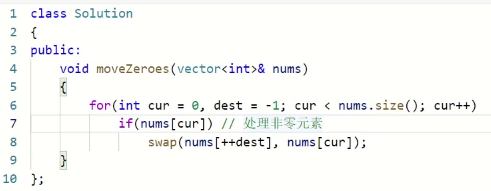
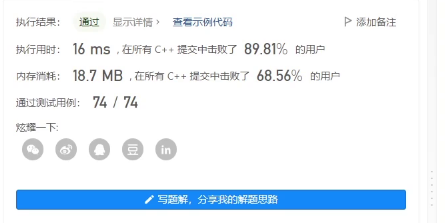
在这里插入图片描述
在这里插入图片描述

我们看一下这里的时间复杂度，一层for循环，cur指针和dest指针之后从前向后移动，
并且只判断cur指针，所以时间复杂度就是cur扫描这个数组一遍就可以时间复杂度就可以划分，
因此我们的时间复杂度肯定是最优的，就是O(N);

1089.复习零

题目解析

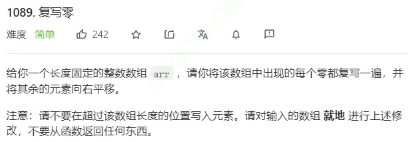
在这里插入图片描述
在这里插入图片描述
读题目，有点抽象，我们举个例子。
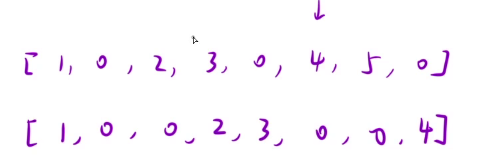
在这里插入图片描述
遍历到4的时候，我们不能往下遍历了，因为数组不能越界。

我们看下一个例子
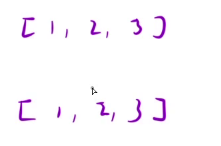
在这里插入图片描述
通过这两个例子，我们就已经知道这道题让我们做什么了。

讲解算法原理

像这种类型的题，在数组中操作数组中元素的题，我们一般也是用双指针算法来解决这种题。
这个双指针算法不是凭空来的。
在这里插入图片描述

举个例子：
我们先不管题目要求，我们非异地操作：
开辟一个数组，来帮助我们完成复写工作。
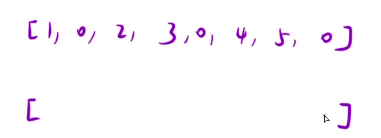
在这里插入图片描述

怎么来呢？
定义一个cur指针，来扫描之前的数组
定义一个dest指针，来表示最重要的那个位置
在这里插入图片描述

当cur指针扫描的时候，要么遇到0元素，要门遇到非0元素，我们分情况讨论，然后把它抄到新的数组里面就可以了。

  1. 当cur扫描遇到非0元素时，仅需在新数组抄写一个，然后cur和dest统一向后移动一位
  2. 当cur扫描遇到0元素时，这时要抄写两个，先在dest位置抄个0，dest移动一位，然后再抄一位， 然后cur和dest统一向后移动一位
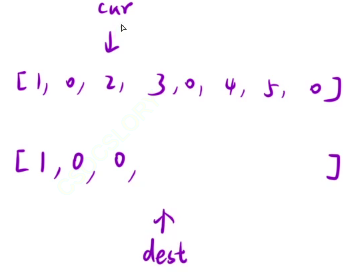
    在这里插入图片描述
    然后依次循环
    在这里插入图片描述

总结一下：
异地操作，定义一个指针指向原始的数组，原后定义一个指针指向新的数组，
一直模拟复写零的操作就可以了。

接下来我们把这个异地操作直接改成就地操作，
我们直接在这个数组模拟就可以了

我们把这两个指针定义到一个数组里面
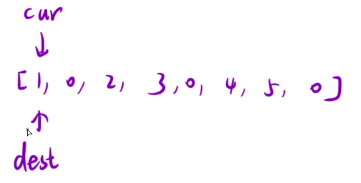
在这里插入图片描述
然后继续重复我们刚刚的操作就可以了。

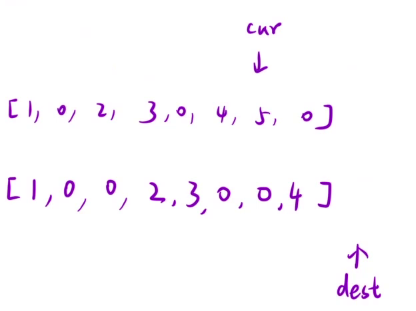
我们先尝试模拟一下：
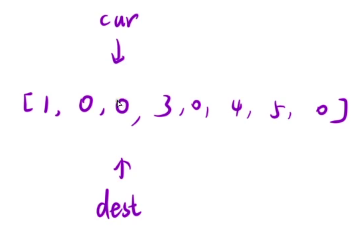
在这里插入图片描述
这样肯定全部都错了，复写零的操作把2给覆盖掉了，后面就全都错了。
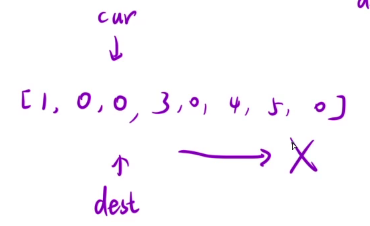
在这里插入图片描述
因此从左向右在这个原地操作的这个过程是不可取的，因为复写零的操作会
覆盖之后的元素，之后的元素还没有抄就被覆盖掉了

但是这道题从左向右不可取，在有些问题必须从左向右，比如之前做过的题，
删除数组中值为val的元素
这道题的优化方式就是，先根据异地操作总结出一段模拟规律，
然后在原地上发现可以用双指针来解决*删除数组中值为val的元素

因为我们这个题是删除，所以dest是在cur前面，
因此绝对不会覆盖掉还没有操作的数
因为我们这道题要复写一个数，
这个dest就有可能跑到后面，就把还没有复写的数都给覆盖掉了

我们再试试从右向左
我们这两个指针刚开始应该定义到哪里呢？
你要抄肯定要抄到最后一个位置, 所以dest指向最后一个位置
cur应该是要指向那个最后一个复写的数
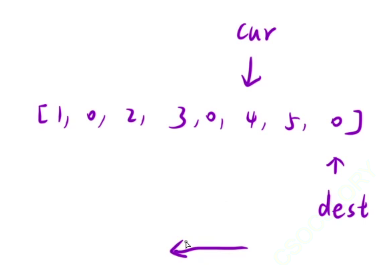
在这里插入图片描述

我们再来试试，如果从后向前的话，能不能完成这个复写操作？
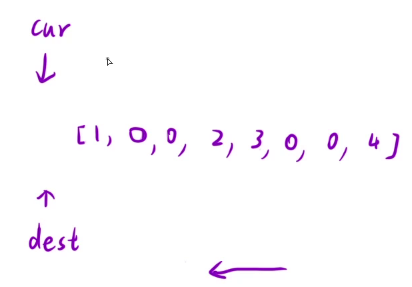
在这里插入图片描述
可以。

总结一下：
在这里插入图片描述

双指针算法嵌套了一个双指针算法。
我们看第一步：
在这里插入图片描述
为什么dest指向-1？
因为我们把dest定义为结果中最后一个位置，因此只需要判断dest是否跑到最后一个位置就可以了。

cur的作用就是从左往右遍历这个数组，决定dest向右移动一步还是两步
我们模拟一下这个过程就可以。
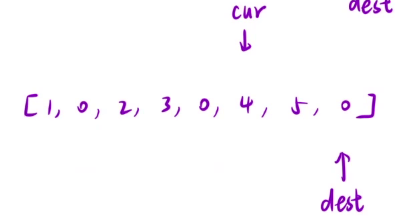
在这里插入图片描述
按照上面这4步，就可以找到dest需要指向的那个位置和cur指向的那个位置。
但是，有个特例：
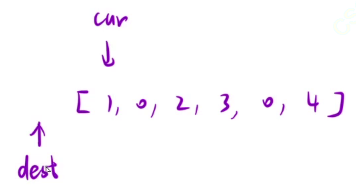
在这里插入图片描述
我们来模拟一下这个例子：
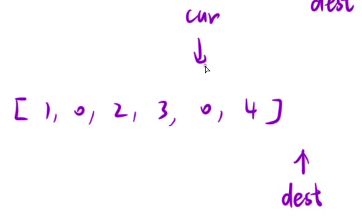
在这里插入图片描述
看cur这个位置是没有问题的，但是cur这个位置是0，导致dest移动的时候发生越界

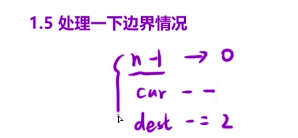
所以我们要再加一步：处理一下边界情况
边界情况就是我们最后要复写的这个数是0
因为我们越界的时候一定是cur==0导致的，所以我们就单独 处理一下这种情况就可以了。

我们来看一下这么处理。
把n-1这个位置修改成0，然后让dest向前移动两步，cur向前移动一步，然后正常复写就可以了
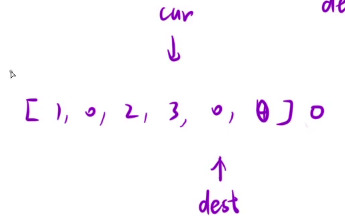
在这里插入图片描述

在这里插入图片描述

总结一下：
这种题算是半模拟题，半双指针算法题，一定要在草稿把它模拟这个过程，不要单单看别人的题解然后知道怎么写，就直接上手写了。

一定要尝试自己手动模拟这个过程，尤其是这个推导，
这样以后在做相似类型的题才能做到举一反三，才能知道怎么去搞，怎么去想，
画图应该怎么画。

编写代码

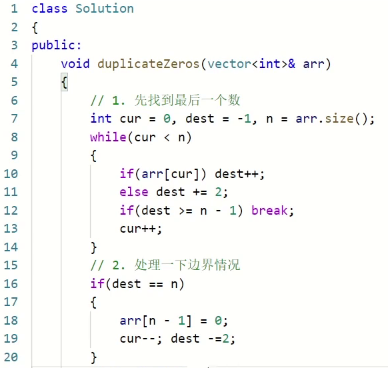
在这里插入图片描述
在这里插入图片描述

202.快乐数

题目解析

这个定义非常重要，如果这个定义你没有搞明白的话，这道题它的难度就不是简单级别了啊，它的难度就可以直逼困难级别了

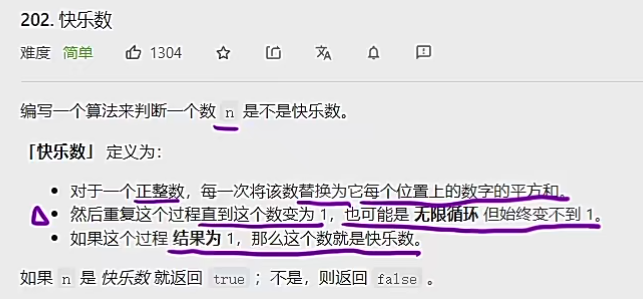
在这里插入图片描述
第二点是最重要的, 直接看可能有点抽象, 我们等下通过两个例子来看一下.

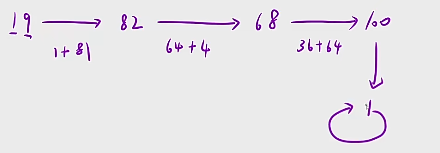
在这里插入图片描述
在这里插入图片描述
只要它变成1，你接下来继续计算的时候，它就是1的平方还是等于1。
所以说这个过程就会在一这里给终止掉.

所以说19这个数，通过这一系列的操作能够变成1 ，因此19这个数就是快乐数, 返回true

这相当于就是我们这个快乐树定义的第二句，第二句的第一种情况就是这个数会变成1

那我们来看看第二种情况就是无限循环，这个情况是什么样子？
在这里插入图片描述
是不是就是一直绕着这个环在转圈？
这就是我们定义的第二种情况，就是这个数可能在这个变化的过程中会陷入到一个环里面，但是在这个环里面是没有1的存在，像这种情况它就属于无限循环，但始终变不到一。

那此时它就不是快乐树，所以说最终返回的结果就是false

相信通过这两个例子，大家已经能搞懂这道题目的要求了，以及什么是快乐树的定义。
接下来啊，我将会带大家来解决这道问题。

讲解算法原理

这道题我们先来看一下它的最终结果

，在快乐树的定义这里, 它告诉我们最终的结果，要么是变成1，要么是无限循环，但始终变不到1
也就是我们事例一和事例二这两种情况

我们把这两种情况给抽象一下

  • 第一种情况就是你这个数一直变，最后变到1
  • 第二种情况就是，你这个数在变化的过程中，然后进入到一个循环里面。 然后在这一个循环里面一直转圈

我们可以把这两种情况抽象成1种情况好，为什么可以抽象我们先来看第一种情况，

第一种情况，虽然你最终的结果到一了，你接下来一变换的时候还是一，因此，第一种情况相当于也有一个环, 只不过你这个环里面所有的数都是1

第二种情况，你所有环里面所有的数都不是一
所以说我们这两种情况可以抽象出来一种。

比如说你这个数变的时候，总会进入到一个循环里面
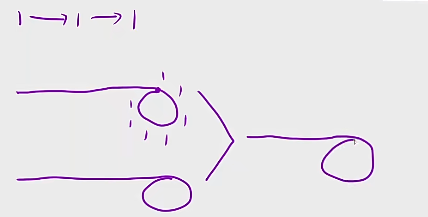
在这里插入图片描述

不知道这个题大家熟悉不熟悉,
我们在学习链表的时候，我们是一定做过一道题的，就是判断链表是否有环.

我们仅需判断这个链表是否有环，在我们这道题里, 我们可以把这个数据抽象成我们之前遇到过那个链表，
因为我们来看你一个数变化成一个数，相当于就是一个数，一个数串了起来，就是相当于一个链表的结构

那我们来看。我们在这里是不用判断链表是否有环，我们仅需判断一下环里面的这个值是多少就可以了，因为我们这两种情况的区分非常明显。

第一种情况也就是说你是快乐树的时候，你这个环里的数都是一
只要你不是快乐数，你只要你环里的所有的数都不是一，

因此我们仅需判断一下我们这个抽象出来这个环里面这个数是否为1就可以了.

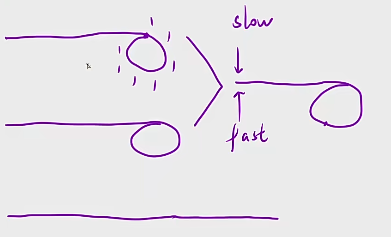
回顾一下，我们当时判断链表是否有环，用的是快慢双指针的方法，因此我们这道题也可以用。
在这里插入图片描述

然后在判断链表是否有环那里，我们仅需判断最后的时候是否相遇就可以了

在我们这里，我们不用判断它们是否相遇，它们两个是一定会相遇的，我们仅需判断他们相遇点的那个数的值就可以了

千万不要被这个双指针里面的指针给限制了你的思维
我们这个双指针仅仅是一种思想，并不是说我们真的要定义指针。
在我们这道题里，我们甚至可以把某一个数当成一个指针

我们觉得这道题简单是基于题目中已经告诉我们第二句话
要么变成一啊，要么无限循环，却始终变不到一，
也就是说我们是仅仅会有这两种情况存在

它没有第二句话，这个时候这个题就恶心了，
也就说它可能会出现第三种情况。
第三种情况可能就是它一直变，里面的这个数永远是不可能重复的，它有可能不是环
在这里插入图片描述

如果加上第三种情况，这个题就难度直接就上来了。

证明

接下来我会来证明一下，就是为什么我们在变化的过程中一定是有环了，接下来全是一个证明的过程。

大家感兴趣可以自己看一下

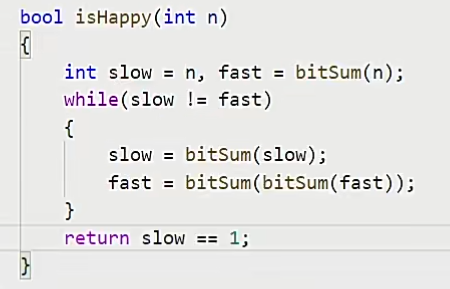
编写代码

因为我们这个题里面会经常用到这个操作，就是求出每个位置上数字的平方和，所以说我们可以把它封装成一个函数
在这里插入图片描述
接下来就是我们的主逻辑
在这里插入图片描述

11.盛最多水的容器

题目解析

在这里插入图片描述

看这个图就很形象。
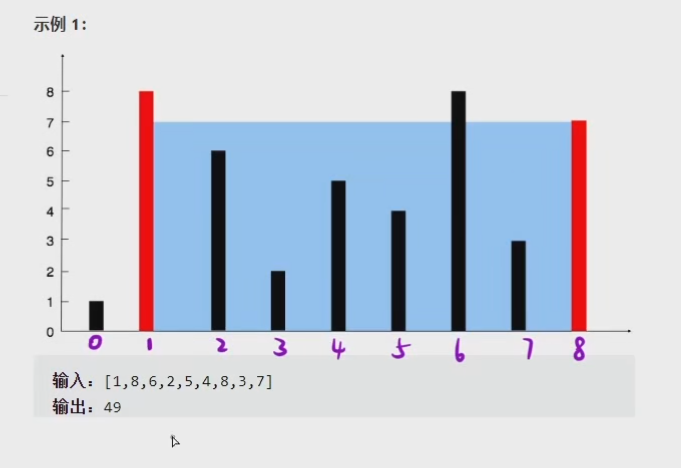
在这里插入图片描述

它相当于告诉给了我们一堆数组，然后每一个数组里面的数都代表着一个高度

在我们这个实例一里面，给了我们这个一个数组，它其实已经把最大的那个容量给我们画出来了。

就是选择一号线以及八号线，我们来计算一下，如果选择一号线和八号线的话，它的容积应该怎么算？

根据木桶效应，水的高度应该是由较低的这个柱子组成的
接下来计算我们的宽度，我们的宽度应该是从一到八这段的距离

讲解算法原理

暴力解法

好好在讲最优解之前，先说一下我们这道题的暴力解法
因为大家刚开始看到一道题的时候， 最先想到的应该就是暴力解法

这道题的暴力解法其实还是非常简单，这道题题目要求是让我们在这个数据范围内选出来两根线组成的容积是最大的

**那我就暴力的把所有的情况都给枚举出来，**那这样我肯定是能找到那个盛水最多的容器

好如何暴力枚举？
其实贼简单，就是两层for循环就可以了。

可以先固定左边这个线，然后依次去枚举右边的线
一直枚举到七这个位置，然后把这所有情况的容积全算出来，
找一个最大值记录一下
在这里插入图片描述

优秀的解法

这个优秀的解法，是通过这个题总结出来的一个规律

规律就是我先随便拿两个数，先只单单研究这个小区间， 看能不能发现一个什么规律
比如说我只先研究这个【6，2，5，4】这个小区间
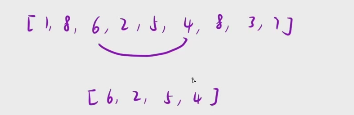
在这里插入图片描述
比如说我刚开始直接拿6跟4来计算容积，我此时的容积的计算公式。
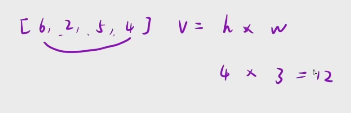
在这里插入图片描述
接下来先别着急乱枚举

如果我拿6跟4计算一下容积之后，
接下来我来看看啊，这个4和2计算，4和5计算的时候会发生什么情况？

我们拿4去和他们算的时候，你会发现这个宽度永远是在减小。
因为我在向内枚举

高度变化会有两种情况：
第一种情况就是我在向内枚举的时候碰见了一个比我小的数，这个高度要减小. 高度要减小，那我乘以一个宽度也减小的，那你的最终结果一定是减小的

第二种情况就是当你碰到一个比你大的数，比你大的数还稍微好一点，稍微好一点就是你的高度是不变的。但是你的宽度永远都是在减小的， 那一个不变的数乘以一个在减小的数，那你的总结果是不是也是在减小的
我要的是盛水最多的容器，那这两根线就不需要枚举了

因为我已经知道了，当我选最左边最右边这两个数算出来一个容积之后，接下来我如果拿这个比较小的数向内枚举的话，我会发现你的容积是一直在减小的， 因此我就可以大胆的在这个小区间内把四给干掉

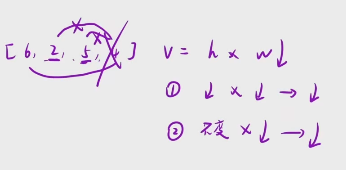
在这里插入图片描述

有了这个规律之后，我们就可以做我们这道题了

其实有那个规律之后，我们就可以把我们的规律扩大，
我直接上来拿最左边这个数。和最右边这个数开干。

如果我直接拿最左边和最右边算出来一个体积v1之后，我们是不是就可以大胆的把这个1给干掉，
因为 接下来1 向内枚举的所有的容积全都是小于v1的

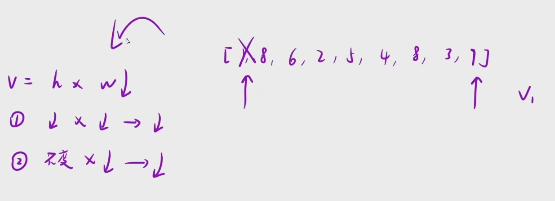
在这里插入图片描述
直接研究下一段区间就可以了， 依次重复
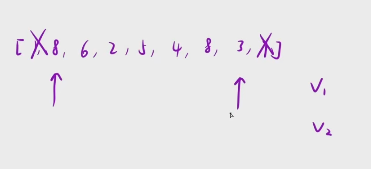
在这里插入图片描述
等我们这两个指针相遇的时候，算出来一大堆的体积，然后在这些体积里面求一个max， 就是我们的最终结果
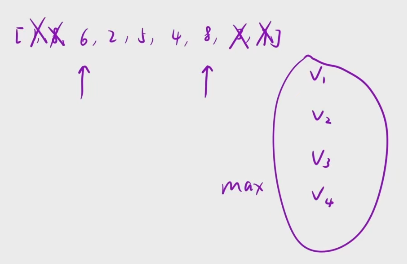
在这里插入图片描述

大家有没有发现我们解法二的时候是不是定义了两个箭头，因此我们的解法二就是用双指针的方法来解决这个问题了

解法二， 利用单调性，使用双指针来解决问题

时间复杂度分析

暴力枚举

优秀解法
如果用双指针解决这个问题的时候，
你会发现这两个指针刚开始是在最左边最右边，
然后每次移动一步，每次移动一步，直到它们两个相遇

所以说此时他们两个就是相当于合伙遍历了整个数组，因此相当于就是遍历数组一遍就找到最终结果

所以说我们利用单调性解决问题的时候，时间复杂度就是O(N)

接下来我们来看一下啊，就是实现我们这个算法的一个细节，就是如何来实现我们这个算法？
其实就是我刚刚的那个模拟过程

准备工作
在这里插入图片描述

我先算出来一个体积v，然后移动指针，这两个指针是向内移动的
根据这两个指针所指的那个线， 谁比较小，谁来移动

如果right小的话，right向里移动一下，然后移动完之后继续算出来一个容积，然后更新我们那个最大值就可以了

一直重复这样的过程，直到这两个指针相遇即可。

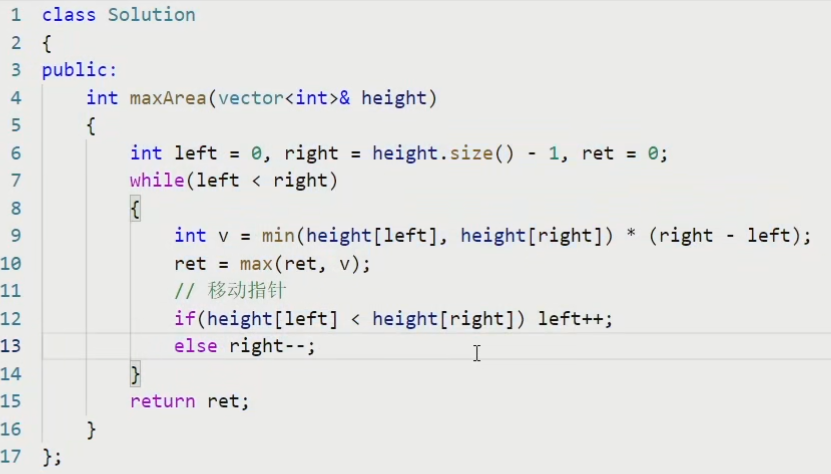
编写代码

在这里插入图片描述

文章来源:https://blog.csdn.net/weixin_68359117/article/details/135299631
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章