定点乘法运算
1. 乘法的手工运算方法
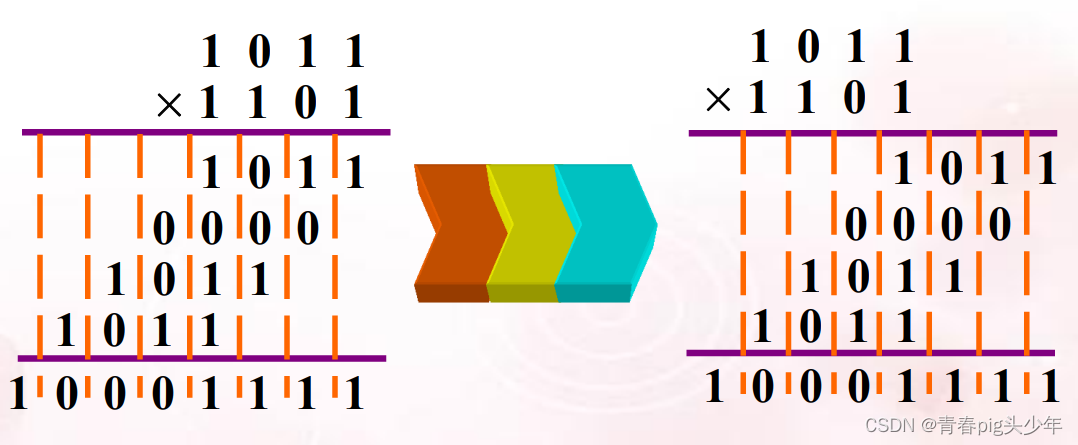
(1)11×13=?
(11)10=(1011)2
(13)10=(1101)2
注:验证下正确性(10001111)2=(143)10,很明显是正确的。
(2)-0.1101×0.1001=?
那我们继续按照上诉的思想来计算
注:同样我们验证下正确性,(-0.1101)2=(-0.8125)10? ?(0.1001)2=(0.5625)10
那么它们的乘积应该是-0.45703125,接着我们看结果再加上两位小数点和符号结果应该是(-0.01110101)2=(-0.45703125)10,很明显,这也是正确的。
小结
- 乘数的每一位对应一个部分积,然后部分积相加得到最后的乘积。
- 部分积很容易确定。当乘数的位是0,其部分积也是0;当乘数的位是1,其部分积是被乘数。
- 部分积通过求和而得到最后乘积,后面的部分积总要比它前面的部分积左移一个位置。
- 两个n位二进制整数的乘法导致其积为2n位长。
2. 定点原码一位乘法?
被乘数左移一位相加变为部分积与被乘数相加后右移一位,将k个部分积同时相加转换为k次“累加与右移”,即每一步只求一位乘数所对应的新部分积, 并与原部分积做一次累加,然后右移一次,这样操作重复k次,得到最后的乘积。
规则
- 参加运算的操作数取其绝对值。
- 令乘数的最低位为判断位,若为“1”,加 被乘数,若为“0”,不加被乘数(加0)。
- 累加后的部分积以及乘数右移一位。
- 重复n次 2 和 3 。
- 符号位单独处理,同号为正,异号为负。
注:通常,乘法运算需要3个寄存器。被乘数存放在B寄存器中;乘数存放在C寄存器中;A寄存器用来存放部分积与最后乘积的高位部分, 它的初值为0。 运算结束后寄存器C中不再保留乘数,改为存放乘积的低位部分。
被乘数:一般指的是乘法前面那个数字
(1)X=+11010,Y=+10110,求Z=X*Y
解:[X]原=0 11010,[Y]原=0 10110
???????乘积的符号位:0
???????乘积的数值部分是两数的绝对值相乘。
???????开始时,部分积为全“0”。
X=+11010
Y=+10110
Z=X×Y=+1000111100
?注:定点原码一位乘法的本质上其实就是加法!!!
有时部分积的符号位出现“1”,并不是出现了负数,而是部分积的值超出了“1”,右移时符号位应补“0”
3. 定点补码一位乘法---布思(Booth)算法
- 参加运算的数用补码表示。
- 符号位参加运算。
- 乘数最低位后面增加一位附加位Yn+1,其初值为0。
- 由于每求一次部分积要右移一位,所以乘数的最低两位Yn、Yn+1的值决定了每次应执行的操作。
- 移位按补码右移规则进行。
- 共需做n+1次累加,n次移位,第n+1次不移位。
规则

由于符号位要参加运算,部分积累加时最高有效位产生的进位可能会侵占符号位,故被乘数和部分 积应取双符号位,而乘数只需要一位符号位。 运算时仍需要有3个寄存器,各自的作用与原码时相同,只不过存放的内容均为补码表示而已。
(1)利用补码一位乘法计算Z=X*Y,其中 X=-0.1101,Y=0.1011。
解:[X]补=11.0011
? ? ? ? [Y]补=0.1011
????????[-X]补=00.1101
????????乘积的数值部分是两数的绝对值相乘。 开始时,部分积为全“0” 。
[X×Y]补=11.01110001
X×Y=-0.10001111
有时部分积的最高符号位出现“1”,右移 时按照补码移位规则补“1”。
Test
(答案我会放评论区)
1、X=0.1101 Y=-0.1011 求X×Y=?
2、X=-0.1110 Y=0.1101 X×Y=?
3、利用补码的运算法则求[X×Y]补,已 知X = +11,Y= – 1011
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Unity Shader 2D血条Sin波纹效果
- 前端常见面试题之异步(event loop, promise, async/await, 宏任务/微任务)
- CHS_04.2.2.3_2+调度器和闲逛进程
- SQL注入是什么呢?
- Docker基础扫盲版——看懂瞬间入门
- python股票分析挖掘预测技术指标知识跳空缺口指标详解(5)
- CleanMyMacX4.14.7清理iTunes垃圾的方法
- windows11通过虚拟机安装Ubuntu20.04
- CNN感受野
- HarmonyOS 应用开发学习笔记 stateStyles:多态样式


