[ToolsChains CPP] Osqp的使用之二:MPCdemo-自动驾驶纵向mpc控制
写在前面
本文是上一篇的后续,https://blog.csdn.net/weixin_46479223/article/details/135070489
本文将先解读官网mpc的例子,
然后实现一个自己设计的mpc的控制器;不远的未来的目标是成为我闭环仿真器(轨迹处理、规划、控制接入基于学习的车辆模型)的一环(目前是pp控制),遥远的未来实现强化学习自动调整参数。
outline
- 官网案例解释
- MPC 自己设计的demo-自动驾驶纵向mpc控制 (理解之后 其实很简单)
- 代码在附件里
官网案例
官网讲解也很清晰,我只做总结和部分重要补充。
关于mpc的理解 和osqp的前置学习 分别在我的文章:
- MPC的acado实现:https://blog.csdn.net/weixin_46479223/article/details/133743263
- osqp eigen 安装和入门使用 :https://blog.csdn.net/weixin_46479223/article/details/135070489

上图是我对mpc的理解简单总结。
 官网案例如上
官网案例如上
官网案例中提到

需要将mpc问题转化为二次规划问题。 这个在Acado文章https://blog.csdn.net/weixin_46479223/article/details/133743263里提到过,如果使用acado的话,它自动帮我们实现了这一步骤,就不需要繁琐的对齐了。而osqp还是需要自己构建。
 构建过程被封装在了这里。
构建过程被封装在了这里。
 构建步骤还是如之前,至此一个mpc问题被构建在了osqp的结构中。
构建步骤还是如之前,至此一个mpc问题被构建在了osqp的结构中。

通过
if (solver.solveProblem() != OsqpEigen::ErrorExitFlag::NoError)
return 1;
问题会被求解,同时以上任何一个步骤出现问题,程序都会返回1。如果希望改变默认设置,可以通过set接口调节,如:
solver.settings()->setWarmStart(true);
可以通过solver的getSolution()接口,把ospq的结果取出来,结果是一个不定长的eigen域下的vector
VectorXd QPSolution = solver.getSolution()
注意
mpc问题并不是一次求解就可以结束:这里针对自动驾驶来说,如果我的控制跑0.02s一个周期,同时规划轨迹为0.1s。那么在每0.02s,我要根据mpc结果外推一次我的新的位置重新计算和参考线的误差,同时也要在每0.02s内设定一定数量的迭代周期(其实可以超过0.02也无所谓)这个称step,在step间我同样需要一个外推方程,来确定这个小step的根据控制量计算的车辆位置的和真实参考的误差。
这其实是两个概念,一个是算法整体的时间步 T,一个是mpc本身迭代优化的时间步 Step。
这里,step osqp无法像acado一样直接通过参数设定需要自己用代码来控。
官网示例用了一个for循环来处理,示例用了50个循环(T),至于step的时间会在矩阵a和b的值中携带,step通过mpcwindows来设定,
// controller input and QPSolution vector
Eigen::Vector4d ctr;
Eigen::VectorXd QPSolution;
// number of iteration steps
int numberOfSteps = 50;
for (int i = 0; i < numberOfSteps; i++)
{
// solve the QP problem
if (solver.solveProblem() != OsqpEigen::ErrorExitFlag::NoError)
return 1;
// get the controller input
QPSolution = solver.getSolution();
ctr = QPSolution.block(12 * (mpcWindow + 1), 0, 4, 1);
// save data into file
auto x0Data = x0.data();
// 可以设置成自己的文件路径,用文件输出流
// propagate the model
x0 = a * x0 + b * ctr;
// update the constraint bound
updateConstraintVectors(x0, lowerBound, upperBound);
if (!solver.updateBounds(lowerBound, upperBound))
return 1;
}
官网教程地址:https://robotology.github.io/osqp-eigen/md_pages_mpc.html
要特别注意他的后三行propagate the model and update the constraint bound,这里的外推和更新其实是在做展示的场景用而和mpc本身无关,属于casebycase的需要自己看情况使用的。我自己的例子中注释掉了,因为我的场景不同。(这一点有问题也请看官大佬们指出)
搭建自己的案例
其实很简单,我们不需要像老王视频里那样推导,直接复用官网结构和转化二次型的公式。重要的是模型的建立。

见上图,我先用纵向做demo(因为我的闭环仿真器还缺一个纵向控制,横向pp先用着展示),关于横向用动力学还是运动学也有很多案例可以直接带入公式了。
由于我在这里展示的demo是开环的,所以差值我设定为恒定,也就相当于自动驾驶的最简单的无限速前车的巡航工况(还句话说 预瞄参数和预瞄信息稳定),同时假定不倒车。
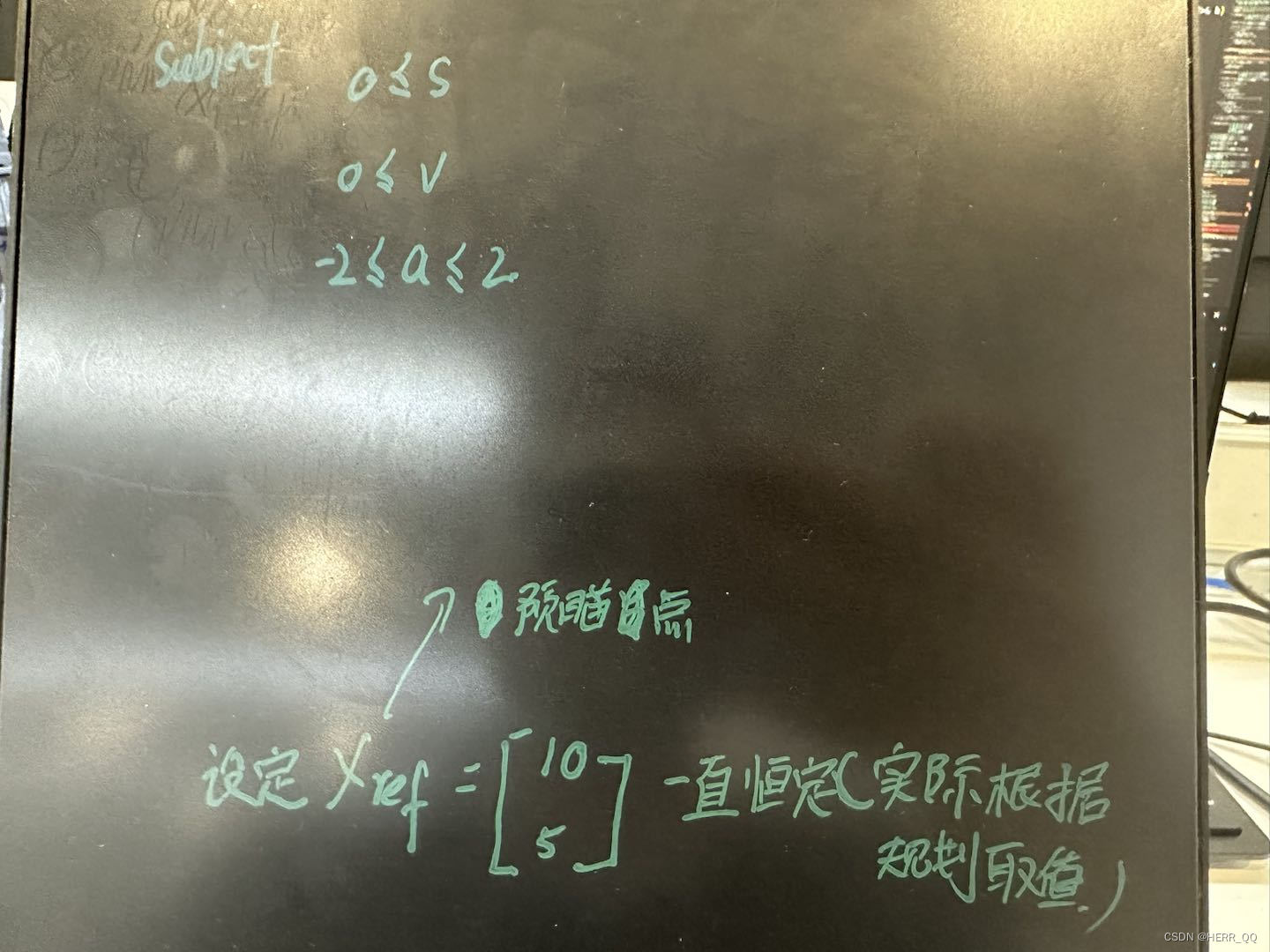 换句话说 在iterator的的循环里,参考信息恒定。
换句话说 在iterator的的循环里,参考信息恒定。
这个循环我理解是进行了一个模拟的过程,每次迭代都模拟系统的响应并更新控制输入,然后通过运行多次迭代来观察系统的跟踪效果。只不过由于我的假设,我的车辆在自动巡航,预瞄准点永远是在我10m前,参考车速永远是5mps
但在mpc自动计算里的误差会在windows减小,mpc根据误差和权重计算的cost来自动迭代找到考虑了整个序列的当下最优解,或者说是我们人为从解序列里去拿出来。
我的mpc代码
借助官网架构可以很方便的搭建出自己的例子,但是注意一点,由于以上我的设定(自动驾驶巡航场景),这三步我需要注释掉,官网的原demo我理解想表现出从起点靠近终末状态的形式,而我这个例子终点相对于起点的位置永远不变化。
运行成功!
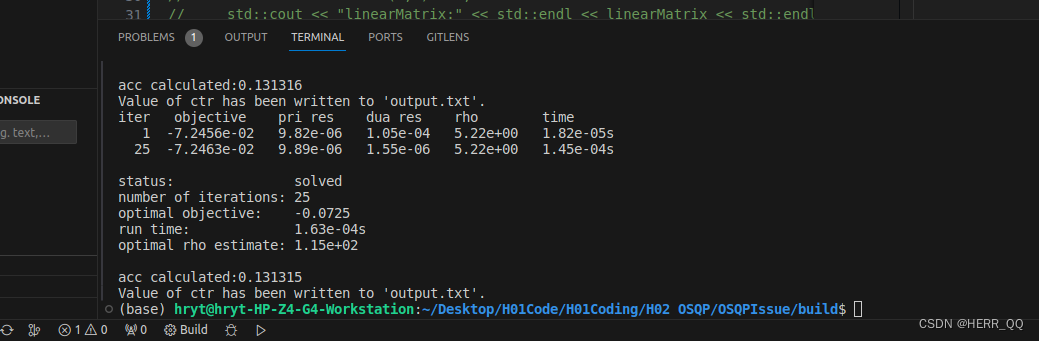 计算结果
计算结果
附录 我的main代码
全代码在我的附件里
int main()
{
// set the preview window
int mpcWindow = 20;
// allocate the dynamics matrices
Eigen::Matrix<double, 2, 2> a;
Eigen::Matrix<double, 2, 1> b;
// allocate the constraints vector
Eigen::Matrix<double, 2, 1> xMax;
Eigen::Matrix<double, 2, 1> xMin;
Eigen::Matrix<double, 1, 1> uMax;
Eigen::Matrix<double, 1, 1> uMin;
// allocate the weight matrices
Eigen::DiagonalMatrix<double, 2> Q;
Eigen::DiagonalMatrix<double, 1> R;
// allocate the initial and the reference state space
Eigen::Matrix<double, 2, 1> x0;
Eigen::Matrix<double, 2, 1> xRef;
// allocate QP problem matrices and vectores
Eigen::SparseMatrix<double> hessian;
Eigen::VectorXd gradient;
Eigen::SparseMatrix<double> linearMatrix;
Eigen::VectorXd lowerBound;
Eigen::VectorXd upperBound;
// set the initial and the desired states
x0 << 0.,0.;
xRef << 10.,5.;
// set MPC problem quantities
setDynamicsMatrices(a, b);
setInequalityConstraints(xMax, xMin, uMax, uMin);
setWeightMatrices(Q, R);
// cast the MPC problem as QP problem
castMPCToQPHessian(Q, R, mpcWindow, hessian);
castMPCToQPGradient(Q, xRef, mpcWindow, gradient);
castMPCToQPConstraintMatrix(a, b, mpcWindow, linearMatrix);
castMPCToQPConstraintVectors(xMax, xMin, uMax, uMin, x0, mpcWindow, lowerBound, upperBound);
// instantiate the solver
OsqpEigen::Solver solver;
// settings
// solver.settings()->setVerbosity(false);
solver.settings()->setWarmStart(true);
// set the initial data of the QP solver
solver.data()->setNumberOfVariables(2 * (mpcWindow + 1) + 1 * mpcWindow);
solver.data()->setNumberOfConstraints(2 * 2 * (mpcWindow + 1) + 1 * mpcWindow);
if (!solver.data()->setHessianMatrix(hessian))
return 1;
if (!solver.data()->setGradient(gradient))
return 1;
if (!solver.data()->setLinearConstraintsMatrix(linearMatrix))
return 1;
if (!solver.data()->setLowerBound(lowerBound))
return 1;
if (!solver.data()->setUpperBound(upperBound))
return 1;
// instantiate the solver
if (!solver.initSolver())
return 1;
// controller input and QPSolution vector
Eigen::VectorXd ctr;
Eigen::VectorXd QPSolution;
// number of iteration steps
int numberOfSteps = 50;
// Open a file for writing
std::ofstream outputFile("output.txt");
for (int i = 0; i < numberOfSteps; i++)
{
// solve the QP problem
if (solver.solveProblem() != OsqpEigen::ErrorExitFlag::NoError)
return 1;
// get the controller input
QPSolution = solver.getSolution();
ctr = QPSolution.block(2 * (mpcWindow + 1), 0, 1, 1);
std::cout<<"acc calculated:"<<ctr<<std::endl;
// save data into file
auto x0Data = x0.data();
// Write the value of ctr to the file
outputFile << "acc calculated: " << ctr << std::endl;
// // propagate the model
// x0 = a * x0 + b * ctr;
// // update the constraint bound
// updateConstraintVectors(x0, lowerBound, upperBound);
// if (!solver.updateBounds(lowerBound, upperBound))
// return 1;
}
// Close the file
outputFile.close();
return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 期货高低板(期货价格飘升,市场掀起高低潮流)
- Linux中的gcc\g++使用
- 实现一个JavaScript动态日期功能
- 数据库操作大全:增删改查、连表查询、函数应用与sql的优化
- 解读 Sobit v2:铭文资产跨链更注重安全、易用性
- 【代码复现】PyTorch获取读取图像的文件名
- 基于SpringBoot+Vue的社区养老监护管理平台(源码+文档+包运行)
- 华清远见嵌入式学习——ARM——作业4
- 中级职称原来有这么多用处!
- 本地源代码运行bun install时报错