“高端”的位运算

王有志,一个分享硬核Java技术的互金摸鱼侠
加入Java人的提桶跑路群:共同富裕的Java人
原计划迭代作为预备知识的收尾,不过在解2的幂和4的幂时,想到关于数字2的问题可以通过位运算去解决,因此补充了关于位运算的内容。
“征服”面试官
当我还在校园的时候,听到过一个故事:某位学长去面试腾讯时,要求优化冒泡排序,学长“苦思冥想”后使用位运算交换变量,成功“征服”面试官拿下Offer。
故事我们可以当做段子来看,不过提到的位运算交换变量却值得我们去探究。先来看下“普通”程序员是如何交换变量的:
int a = 3, b = 5;
int temp = a;
a = b;
b = temp;
那么“高端”程序员是如何使用位运算交换变量的呢?
int a = 3, b = 5;
a = a ^ b;
b = a ^ b;
a = a ^ b;
同样是4行代码,使用位运算无需引入临时变量,因此在空间复杂度上更优,并且位运算更靠近计算机,因此在运算效率上更有优势。
位运算
计算机中,数以二进制的形式存储在内存中,而位运算就是对内存中的二进制数进行操作。维基百科中是这样定义的:
位操作是程序设计中对位数组或二进制数的一元和二元操作。在许多古老的微处理器上,位运算比加减运算略快,通常位运算比乘除法运算要快很多。在现代架构中,位运算的运算速度通常与加法运算相同(仍然快于乘法运算),但是通常功耗较小,因为资源使用减少。
既然位运算是操作二进制数的,那么我们有必要先了解计算机中二进制数是如何表示的。
码,反码和补码
计算机中有3种有符号数的表示方法:原码,反码和补码。
原码,反码和补码的共同点是:最高位为符号位,0代表正数,1代表负数。但它们在数值位上有着不同的表示方法。
我们通过十进制数字-11,来展示这3种表示方法的二进制数(使用8位)。
原码表示
使用原码表示时,除了符号位外,数值位和我们通过“除二倒取余法”计算后的数字相同,-11的原码为:1000 1011。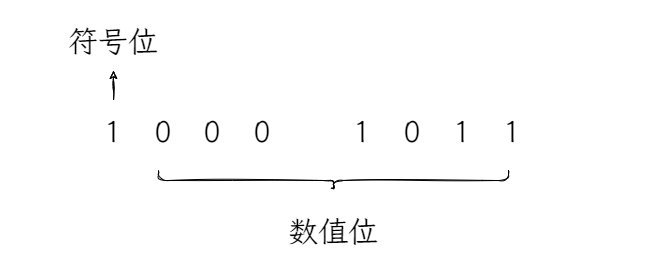
反码表示
反码是原码和补码之间转换的过渡码,原码转换为反码的规则为:
- 正数时,反码和原码相同;
- 负数时,符号位保持不变,数值位时原码按位取反。
因此,-11的反码表示为:1111 0100。
补码表示
通过反码,我们可以计算出数字的补码,转换规则为:
- 正数时,补码和反码相同;
- 负数时,符号位保持不变,数值位时反码数值位加1。
因此,-11的补码表示为:1111 0101。
补码是计算机系统中普遍使用的表示方式,补码相较于原码和反码有两个特点:
- 符号位可以参与运算;
- 加法和减法可以统一处理。
到此为止,我们已经了解了计算机中3种二进制数的表示方式,下面简单的做个总结:当数字为正数时,原码,反码和补码相同。
当数字为负数时,原码,反码和补码遵循以下转换规则: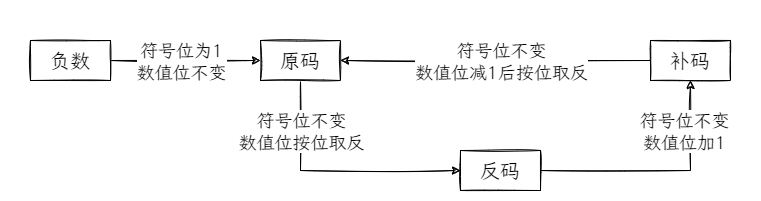
位运算符
Java中提供了7种位运算操作符:
| 符号 | 描述 | 运算规则 | 优先级 | 示例 |
|---|---|---|---|---|
| ~ | 取反 | 操作一个数,0变为1,1变为0 | 1 | ~ a |
| << | 带符号左移 | 操作两个数,数值位向左移动,高位丢弃,低位补0 | 2 | a << 1 |
| >> | 带符号右移 | 操作两个数,数值位向右移动,低位丢弃,高位补符号位 | 2 | a >> 1 |
| >>> | 无符号右移 | 操作两个数,数值位向右移动,低位丢弃,高位补0 | 2 | a >>> 1 |
| & | 按位与 | 操作两个数,同为1时,结果为1,否则为0 | 3 | a & b |
| ^ | 按位异或 | 操作两个数,相同为0,不同为1 | 4 | a ^ b |
| | | 按位或 | 操作两个数,同为0时,结果为0,否则为1 | 5 |
用一段程序来展示位运算符的基础操作:
int number = -11;
// 输出Java中的二进制表示(补码),11111111111111111111111111110101
System.out.println("原值,二进制:" + Integer.toBinaryString(number));
// 取反,0变为1,1变为0
System.out.println("取反,十进制" + ~number);
System.out.println("取反,二进制:" + Integer.toBinaryString(~number));
// 按位异或,相同为0,不同为1
System.out.println("按位异或" + (number ^ number));
// 按位与,同为1时,结果为1,否则为0
System.out.println("按位与:" + (number & 1));
// 按位或,同为0时,结果为0,否则为1
System.out.println("按位或:" + (number | ~number));
// 左移,数值位向左移动,高位丢弃,低位补0
System.out.println("左移,十进制:" + (number << 1));
System.out.println("左移,二进制:" + Integer.toBinaryString(number << 1));
// 右移,数值位向右移动,低位丢弃,高位补符号位
System.out.println("右移,十进制:" + (number >> 2));
System.out.println("右移,二进制:" + Integer.toBinaryString(number >> 2));
// 无符号右移,数值位向右移动,低位丢弃,高位补0
System.out.println("无符号右移,十进制:" + (number >>> 1));
System.out.println("无符号右移,二进制:" + Integer.toBinaryString(number >>> 1));
位运算技巧
到目前为止,我们已经了解了二进制数和位运算符,不过这些操作看起平平无奇,好像并没有什么用?那么接下来就介绍一些基础的位运算技巧。
2的幂
还记得2的幂吗?当时使用递归求解,效率上还是有些差强人意的,那么有没有更高效的方法呢?
有一个二进制数字:1101 0101。根据常规的二进制转换为十进制的方法,可以得到如下等式:
1
×
2
7
+
1
×
2
6
+
0
×
2
5
+
1
×
2
4
+
0
×
2
3
+
1
×
2
2
+
0
×
2
1
+
1
×
2
0
=
213
1\times2^7+1\times2^6+0\times2^5+1\times2^4+0\times2^3+1\times2^2+0\times2^1+1\times2^0=213
1×27+1×26+0×25+1×24+0×23+1×22+0×21+1×20=213
显而易见,如果是2的幂,二进制数字中有且仅有1个1。例如:1000 0000。那么判断是否为2的幂就变成了证明二进制数字仅有1个1,或者说是,证明二进制数字中1后面所有位都为0。
如果数字n是2的幂,那么n-1一定是比n少一位,且二进制位都为1的数字。可以利用0&1=0的特性判断是否符合我们的预期,代码如下:
if((n & (n - 1)) == 0) {
return true;
} else {
return false;
}
奇偶性
此外,在二进制转换为十进制的过程中,还可以得到另外一点信息,即如果二进制的最低位为1,则数字为奇数。
那么在判断一个数字的奇偶性时,我们只需要得知二进制数字的最后一位是否为1即可,代码如下:
if ((number & 1) == 0) {
System.out.println("偶数");
} else {
System.out.println("奇数");
}
快速乘/除2
还是在二进制转换为十进制的过程中,我们可以看到,如果想要乘/除2,只需要向左/右移动一位即可,不过对于奇数来说是除2后向下取整。
今天介绍的只是位运算中的基础技巧,算是为大家抛砖引玉。实际上位运算的技巧远不止这些,或者说是二进制数的使用技巧远不止这些。
离我们最近的有Java中ThreadPoolExecutor处理线程状态时使用的技巧,或者叫做位掩码。另外,相信有的小伙伴在面试中被问到过布隆过滤器,这也是一种二进制的进阶用法。
更多的技巧,也可以参考位运算的简单应用和位运算的进阶介绍。
结语
今天的内容到这里就结束了,我们来回顾下都聊了哪些内容:
首先是简单介绍了计算机中的原码,反码和补码,接着是Java中7种位运算操作符,不过并不是所有语言都提供了无符号右移(>>>),最后介绍了一些简单位运算的技巧,但位运算的用法远不止这些,包括听起来很高端的布隆过滤器,也使用了位运算,这也是为什么我说位运算“高端”。
最后补充一篇关于为什么要使用位运算的问答《What are the advantages of using bitwise operations?》,虽然已经过去了11年,但依旧可以作为参考。
练习
因为后面很少会再出现位运算的内容了,因此这次的题目会比较多。
简单难度:
中等难度:
如果本文对你有帮助的话,还请多多点赞支持。如果文章中出现任何错误,还请批评指正。最后欢迎大家关注分享硬核Java技术的金融摸鱼侠王有志,我们下次再见!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- CentOS 7 安装&配置MySQL
- 自定义线程池核心参数讲解
- 零基础学Python(2)— 安装Python开发工具之PyCharm
- CNN——GoogLeNet
- 八. 实战:CUDA-BEVFusion部署分析-学习spconv的优化方案(Explicit GEMM conv)
- pandas中,DataFrame.sample 的理解:
- 论文笔记_Generic_InP-Based_Integration_Technology:_Present_and_Prospects
- Copilot概述:AI助手引领编程新纪元
- Qt QProgressBar进度条控件
- 紫外加速老化试热冲击试验箱