统计学-R语言-3

---

前言

本篇文章是介绍对数据的部分图形可视化的图型展现。

---

给直方图增加正态曲线的不恰当之处

需要注意的是，给直方图拟合正态分布曲线并非总是适用，有时甚至是荒谬的，容易产生误导。合理的做法是为直方图拟合一条核密度估计曲线，它是数据实际分布的一种近似描述。
下面通过一个实际例子说明给直方图拟合正态分布曲线的荒谬之处：
根据美国黄石国家公园（Yellowstone National Park）老忠实间歇喷泉（Old Faithful Geyser）数据绘制的直方图，并在直方图中分别增加了核密度估计曲线和正态分布曲线。

par(mai=c(.8,.8,.1,.1),cex=.8)
hist(faithful$eruptions, probability=TRUE, xlab="喷发持续时间",breaks=20, col="light blue",main="")
rug(faithful$eruptions)
lines(density(faithful$eruptions, bw=.1), type='l', lwd=2, col='red')
points(quantile(faithful$eruptions),c(0,0,0,0,0),lwd=5,col="red2")
points(mean(faithful$eruptions),c(0),lwd=8,col=4)
curve(dnorm(x,mean=mean(faithful$eruptions),sd=sd(faithful$eruptions)),add=T,col="blue",lwd=2,lty=6)

图显示有两个明显的峰值，用核密度估计曲线可清晰地看出喷发持续时间属于双峰分布，可见为该直方图拟合正态分布曲线的荒之处。

直方图与条形图的区别

条形图中的每一矩形表示一个类别，其宽度没有意义；
直方图的宽度则表示各组的组距分组数据具有连续性，直方图的各矩形通常是连续排列；
而条形图则是分开排列条形图主要用于展示类别数据，而直方图则主要用于展示数值数据。

核密度图

核密度估计（density estimation）是根据一定的核（kernel）函数和适当的带宽（band-width）对数据的分布密度做出的估计。
核密度图（kernel density plot）是对核密度估计的一种描述，利用该图可看出数据的实际分布状况.以例2-3的数据为例，绘制6名运动员射击成绩核密度估计曲线。
R代码和结果如下所示：

# 用lattice包绘制核密度曲线
load("C:/example/ch2/example2_3_1.RData")
library(lattice)
dp1<-densityplot(~射击环数|运动员,data=example2_3_1,col="blue",cex=0.4,par.strip.text=list(cex=0.6),sub="(a)栅格图")

# 用lattice包绘制例2-3的核密度比较曲线
dp2<-densityplot(~射击环数,group=运动员,data=example2_3_1,auto.key=list(columns=1,x=0.01,y=0.95,cex=0.6),cex=0.4,sub="(b)比较图")
# 组合latiice包的绘图
plot(dp1,split=c(1,1,2,1))
plot(dp2,split=c(2,1,2,1),newpage=F)

该图显示了每名运动员射击成绩分布的核密度估计曲线（图中的“ o”为扰动点）。

load("C:/example/ch2/example2_3_1.RData")
attach(example2_3_1)
library(sm)
par(cex=0.8,mai=c(.7,.7,.1,.1))
sm.density.compare(射击环数,运动员,lty=1:6,col=c("black","blue","brown","darkgreen","green","red"),lwd=2)
legend("topleft",legend=levels(运动员),lty=1:6,,col=c("black","blue","brown","darkgreen","green","red"))

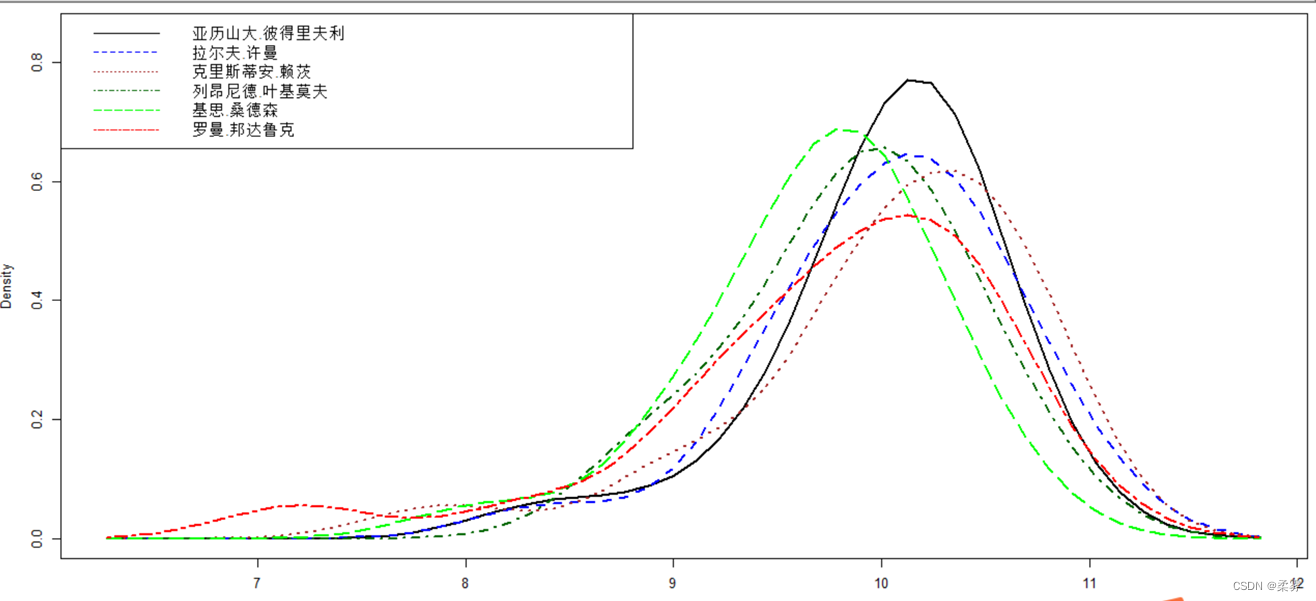
该图显示了6名运动员射击成绩分布的核密度估计比较曲线容易看出，6名运动员射击成绩均呈现左偏分布。这是因为射击环数的中心点是10.99.环数的上界已被限定，而下界（0环）则远离中心点.因此，下界值方向出现远离中心点的环数的可能性大于上界值方向。此外，从6名运动员射击成绩的分布看，除了基思桑德森，其他运动员射击成绩的分布中心均很接近最高环数（10.99）。

时间序列图

load("C:/example/ch2/example2_9.RData")
example2_9<-ts(example2_9,start=2000)
par(mai=c(0.7,0.7,0.1,0.1),cex=0.8,fg=2) 
plot(example2_9[,2],lwd=2,ylim=c(2000,30000),xlab="年份",ylab="居民消费水平",type="n")
grid(col="gray60")
points(example2_9[,2],type='o',lwd=2,ylim=c(2000,30000),xlab="年份",ylab="居民消费水平")
lines(example2_9[,3],type='b',lty=2,lwd=2,col="blue")
legend(x="topleft",legend=c("农村居民消费水平","城镇居民消费水平"),lty=1:2,col=c(1,4),cex=0.8)

函数ts（data， start，…）用于创建时间序列对象，参数data为向量、矩阵或数据框； start设定时间序列的起始时间。

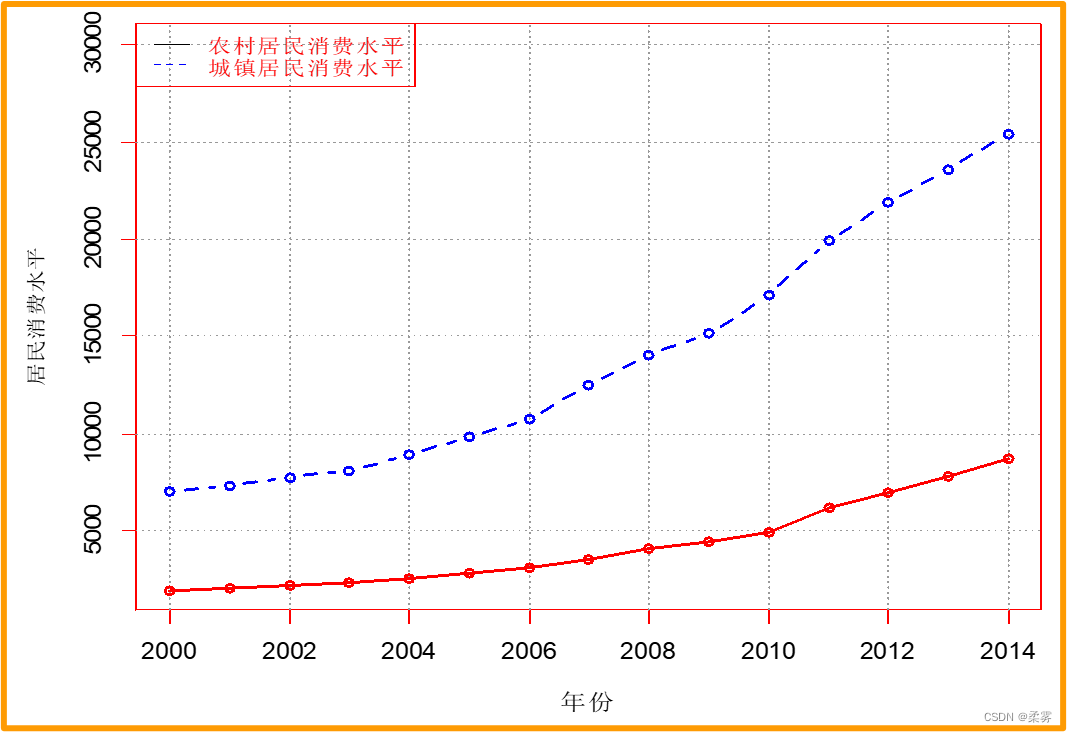
图显示，无论是农村居民还是城镇居民，消费水平随时间的推移均呈现逐年提高的趋势，但城镇居民的消费水平各年均高于农村居民，而且随时间的推移消费水平的差距有扩大的趋势。

洛伦茨曲线

在频数分布中，如果将各类别的频数逐级累加，即可得到累积频数分布表。根据累加频数分布表可以绘制累加频数分布曲线。
洛伦茨曲线（Lorenz curve）是一种特殊的累积频数分布曲线，它是20世纪初由美国统计学家洛伦茨(M. E. Lorentz)根据意大利经济学家帕累托(V. Pareto)提出的收入分配公式绘制的描述收入和财富分配不平等程度的曲线。

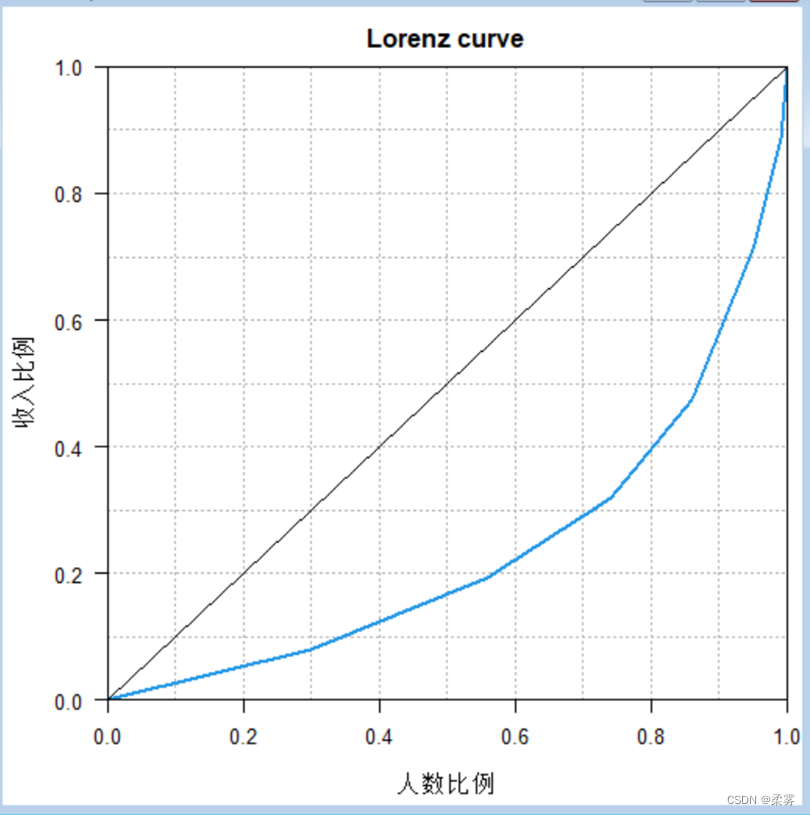
图中弯曲的线就是洛伦茨曲线
如果用横轴表示人口百分比，纵轴表示相应人口获得的收入百分比，通过洛伦兹曲线，可以直观地反映一个国家或地区收入分配平等或不平等的状况
如果一定累积百分比的人口获得相同累积百分比的收入，就是图中的对角线，即收入分配绝对平均线。
如果绝大多数人口占有很少的收入，而一小部分人口占有绝大部分的收入，则洛伦茨曲线就靠近下横轴和右纵轴形成弯曲的线。弯曲程度越大，表示收入分配越不公平。

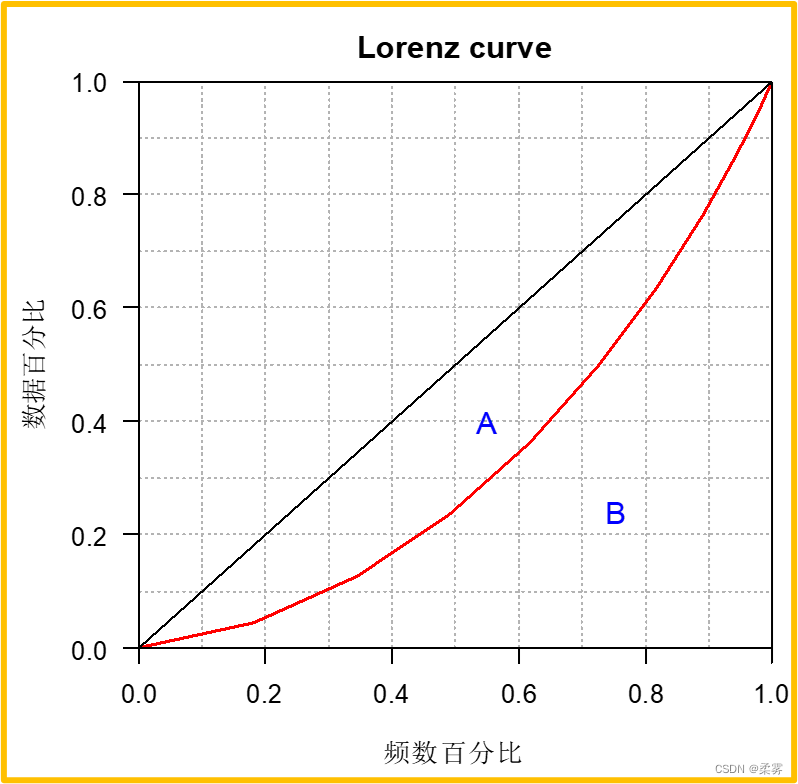
为更准确的反映收入分配的不平等程度，20世纪初意大利经济学家基尼(C. Gini)根据洛伦茨曲线给出了衡量收入分配平等程度的指标，即基尼系数(Gini coefficient)，用公式表示为：

计算绘制洛伦茨曲线所需的各百分比数值

load("C:/example/ch2/example2_10.RData")
library(DescTools)
Lc(example2_10$组中值,example2_10$人数)

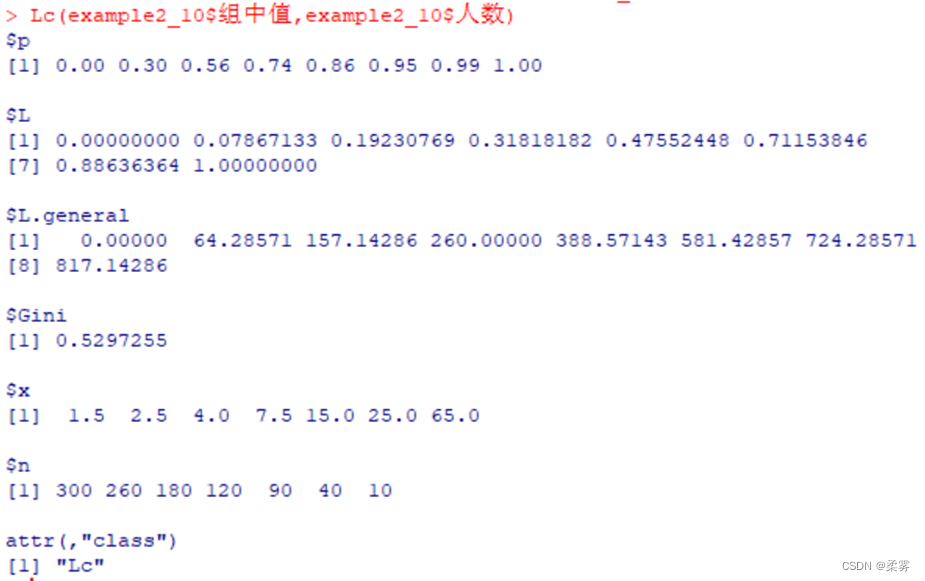
绘制洛伦茨曲线

par(mai=c(0.7,0.7,0.4,0.1),cex=0.8)
plot(Lc(example2_10$组中值,example2_10$人数),xlab="人数比例",ylab="收入比例",col=4,panel.first=grid(10,10,col="gray70"))

---

练习

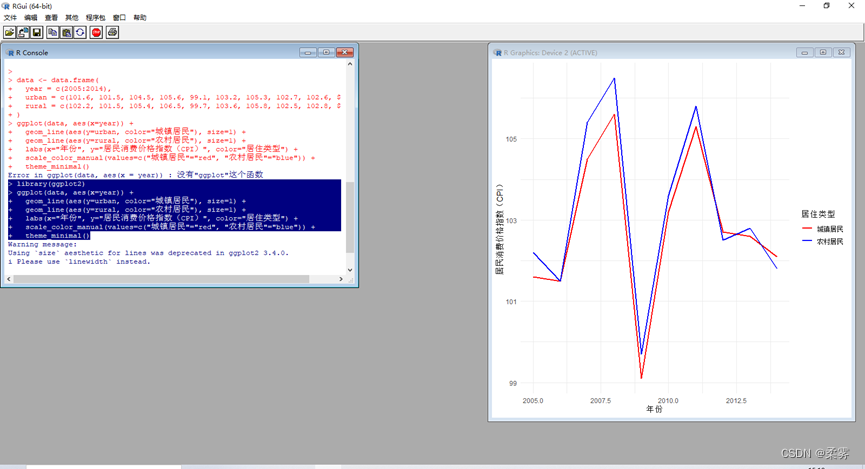
1、（数据： exercise2_5.RData）exercise2_5.RData数据是2005—2014年我国城镇居民和农村居民的居民消费价格指数（CPI）数据。
绘制时间序列图，观察城镇居民和农村居民消费价格指数的变化特征。

library(ggplot2)
ggplot(data, aes(x=year)) geom_line(aes(y=urban, color="城镇居民"), size=1)  geom_line(aes(y=rural, color="农村居民"), size=1) + abs(x="年份", y="居民消费价格指数（CPI）", color="居住类型") scale_color_manual(values=c("城镇居民"="red", "农村居民"="blue"))  theme_minimal()

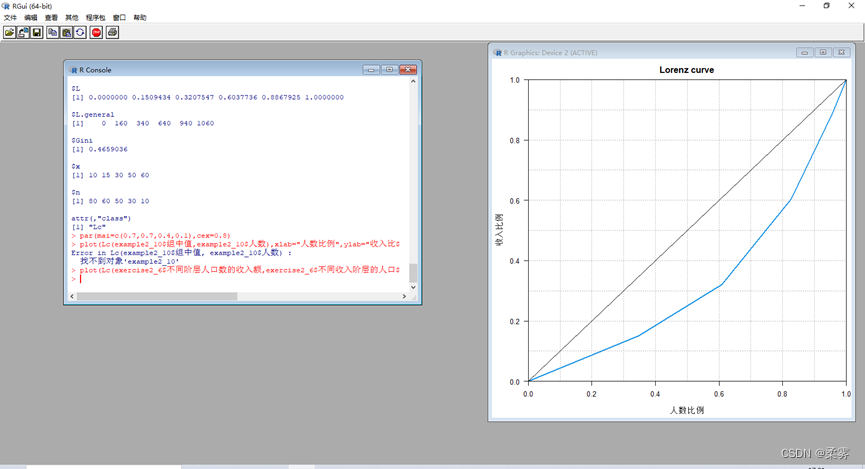
2、（数据： exercise2_6.RData）假定某地区不同收入阶层的人口数和不同阶层人口的年收入额如数据 exercise2_6.RData所示。
绘制洛伦兹曲线分析收入分配的不平等程度。

load("C:/ch2/ch2/exercise/exercise2_6.RData")
library(DescTools)
Lc(exercise2_6$不同阶层人口数的收入额,exercise2_6$不同收入阶层的人口数)
par(mai=c(0.7,0.7,0.4,0.1),cex=0.8)
plot(Lc(exercise2_6$不同阶层人口数的收入额,exercise2_6$不同收入阶层的人口数),xlab="人数比例",ylab="收入比例",col=4,panel.first=grid(10,10,col="gray70"))