【算法分析与设计】最短路径和

题目：

给定一个包含非负整数的?m?x?n?网格?grid?，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

?示例：

示例 1：

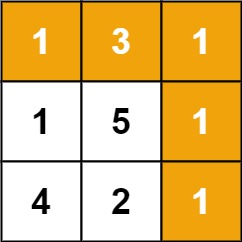
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

思想（动态规划）

动态规划是分治思想的延伸，通俗一点来说就是大事化小，小事化无的艺术

在将大问题化解为小问题的分治过程中，保存对着些小问题已经处理好的结果，并供后面处理更大规模的问题时直接使用这些结果

动态规划具备了以下三个特点

1.把原来的问题分解成了几个相似的子问题

2.所有的子问题都只需解决一次

3.存储子问题的解

动态规划的本质

是对问题状态的定义和状态转移方程的定义（状态以及状态之间的递推关系）

动态规划问题一般从以下四个角度考虑：

1.状态定义

2.状态间的转移方程定义

3.状态的初始化

4.返回结果

状态定义的要求：定义的状态一定要形成递推关系

适用场景：最大值/最小值 ，可不可行， 是不是，方案个数?

算法分析与设计

步骤一、定义数组元素的含义

由于我们的目的是从左上角到右下角，最小路径和是多少，那我们就定义 dp[i] [j]的含义为：当走到(i, j) 这个位置时，最小的路径和是 dp[i] [j]。那么，dp[m-1] [n-1] 就是我们要的答案了。

注意，这个网格相当于一个二维数组，数组是从下标为 0 开始算起的，所以 由下角的位置是 (m-1, n - 1)，所以 dp[m-1] [n-1] 就是我们要走的答案。

步骤二：找出关系数组元素间的关系式

一种是从 (i-1, j) 这个位置走一步到达

一种是从(i, j - 1) 这个位置走一步到达

不过这次不是计算所有可能路径，而是计算哪一个路径和是最小的，那么我们要从这两种方式中，选择一种，使得dp[i] [j] 的值是最小的，显然有

dp[i]?[j]?=?min(dp[i-1][j]，dp[i][j-1])?+?arr[i][j];//?arr[i][j]?表示网格种的值

步骤三、找出初始值

显然，当 dp[i] [j] 中，如果 i 或者 j 有一个为 0，那么还能使用关系式吗？答是不能的，因为这个时候把 i - 1 或者 j - 1，就变成负数了，数组就会出问题了，所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的，相当于计算机图中的最上面一行和左边一列。因此初始值如下：

dp[0] [j] = arr[0] [j] + dp[0] [j-1]; // 相当于最上面一行，只能一直往左走

dp[i] [0] = arr[i] [0] + dp[i] [0]; ?// 相当于最左面一列，只能一直往下走

代码实现

class Solution {
    public int minPathSum(int[][] grid) {
        int col=grid[0].length;
        int row=grid.length;
        if(row<0||col<0){
            return -1;
        }
        int[][] dp=new int[row][col];

           dp[0][0]=grid[0][0];

        for(int i=1;i<col;i++){

            dp[0][i]=grid[0][i]+dp[0][i-1];
           
        }
         for(int i=1;i<row;i++){

            dp[i][0]=grid[i][0]+dp[i-1][0];
            
        }
     
        for(int i=1;i<row;i++)
            for(int j=1;j<col;j++){
                dp[i][j]=Math.min(dp[i][j-1],dp[i-1][j])+grid[i][j];
            }
        return dp[row-1][col-1];

    }
}

运行结果