F-score 和 Dice Loss 原理及代码

通过看开源图像语义分割库的源码，发现它对 Dice Loss 的实现方式，是直接调用 F-score 函数，换言之，Dice Loss 是 F-score的特殊情况。于是就研究了一下这背后的原理，作文以记之。

1. F-score

1. 1 原理

首先介绍 F-score：

要理解F-score，就要先回顾一下 Precision 和 Recall，首先给出公式：

这两个指标衡量算法的准确性时，通常是相互排斥的。例如，输入一个数据，算法根据数据预测一个分数，现在为该分数设定阈值，大于阈值的预测为真，小于该阈值的预测为假。

• 如果这个阈值得过低，低到测试集中所有的样本均判定为真，那么此时，FN=0（False negative, 压根就没有预测出来 negative 的样本），代入公式 (2) 得 Recall = 1。但此时，预测为真的样本中，包含大量的 FP，即 False Positive，将会导致 Precision 过低。
• 如果这个阈值设置得过高，使得所有被判定为正的样本都是真的，那么 FP=0，Precision=1，此时将不可避免有很多本应被判定为正的样本，被错误地判定为负，也就是 FN 很大，导致 Recall 过低。

在不同的应用场景下，对这两个指标的侧重不同。例如新冠感染者检测，就应该尽量提高 Recall，务求没有漏网之鱼。但在检测垃圾邮件时，应该尽量提升 Precision，即每个被判定为垃圾邮件的，都是板上钉钉毫无争议的，防止出现误伤，把正常邮件当成垃圾邮件处理。

F-score 则是将这两个指标综合起来：

• $\beta$控制 Precision 和 Recall 的重要程度, 当$\beta =1$, 对应 F1-score，此时 Precision 和 Recall 同样重要。

• $\beta$两个常用的取值是 0.5 和 2，当取 0.5 时，Precision 对 F-score 的影响更大，当取 2 时，Recall 对 F-score 的影响更大。(可以考虑得更极端一点，当$\beta \to 0$，公式(3)趋于 Precision;当$\beta \to \infty$，公式(3)上下同除以分子，易知其将趋于 Recall)

最后，把 (1) (2) 代入 (3) 得：

1. 2 代码

def f_score(inputs, target, beta=1, smooth = 1e-5, threhold = 0.5):
    n, c, h, w = inputs.size()
    nt, ht, wt, ct = target.size()
    if h != ht and w != wt:
        inputs = F.interpolate(inputs, size=(ht, wt), mode="bilinear", align_corners=True)
        
    temp_inputs = torch.softmax(inputs.transpose(1, 2).transpose(2, 3).contiguous().view(n, -1, c),-1)
    temp_target = target.view(n, -1, ct)

    #--------------------------------------------#
    #   计算dice系数
    #--------------------------------------------#
    temp_inputs = torch.gt(temp_inputs, threhold).float()
    tp = torch.sum(temp_target[...,:-1] * temp_inputs, axis=[0,1])
    fp = torch.sum(temp_inputs                       , axis=[0,1]) - tp
    fn = torch.sum(temp_target[...,:-1]              , axis=[0,1]) - tp

    score = ((1 + beta ** 2) * tp + smooth) / ((1 + beta ** 2) * tp + beta ** 2 * fn + fp + smooth)
    score = torch.mean(score)
    return score

• inputs为分割模型的预测输出，未经过softmax, target为gt
• temp_target中将channels维度设为num_classes+1，为了方便处理白边，因此在实际计算时需要去掉最后一个channel: temp_target[...,:-1]
  
• 预测分割图temp_inputs与 GT 分割图的点乘，然后再(n,hw)方向上求和作为tp
  参考自: Dice系数(Dice coefficient)与mIoU与Dice Loss
  
• 因为预测temp_inputs (pred) = fp+tp, 因此已知temp_inputs和tp, 就可以求出fp
• 同理temp_target (gt) = fn+tp, 因此已知temp_target和tp, 就可以求出`fn
• 然后根据F-score的计算公式，在已知tp,fp,fn以及beta系数，就可以计算出F-score值了
  

    score = ((1 + beta ** 2) * tp + smooth) / ((1 + beta ** 2) * tp + beta ** 2 * fn + fp + smooth)
    score = torch.mean(score)

2. Dice Loss

2.1 原理

Dice Loss 是语义分割中常用的一种损失，它的计算方法如下：

即，分子为预测值与真实值的交集元素数目的两倍，分母为两个集合元素数目之和（注意并不是并集，而是和）。而

因此，(6) 相当于：
$$1?\frac{2TP}{2TP+FP+FN}$$

而上式的结果，正是公式 (5) 中$\beta =1$的情况,也就是F1 score。因此，

Dice Loss = 1 - F1 score 

2.2 代码

def Dice_loss(inputs, target, beta=1, smooth = 1e-5):
    n, c, h, w = inputs.size()
    nt, ht, wt, ct = target.size()
    if h != ht and w != wt:
        inputs = F.interpolate(inputs, size=(ht, wt), mode="bilinear", align_corners=True)
        
    temp_inputs = torch.softmax(inputs.transpose(1, 2).transpose(2, 3).contiguous().view(n, -1, c),-1)
    temp_target = target.view(n, -1, ct)

    #--------------------------------------------#
    #   计算dice loss
    #--------------------------------------------#
    tp = torch.sum(temp_target[...,:-1] * temp_inputs, axis=[0,1])
    fp = torch.sum(temp_inputs                       , axis=[0,1]) - tp
    fn = torch.sum(temp_target[...,:-1]              , axis=[0,1]) - tp

    score = ((1 + beta ** 2) * tp + smooth) / ((1 + beta ** 2) * tp + beta ** 2 * fn + fp + smooth)
    dice_loss = 1 - torch.mean(score)
    return dice_loss

• 可以看到dice_loss的实现，跟F-score基本上是一模一样的, 将torch.mean(score)求得的F-soce, 然后通过dice_loss = 1- F-score 来实现。
• 代码中默认$\beta =1$, 所以更精确的说： dice_loss = 1- F1-score
• DIce _loss的在训练损失中的使用如下:
  

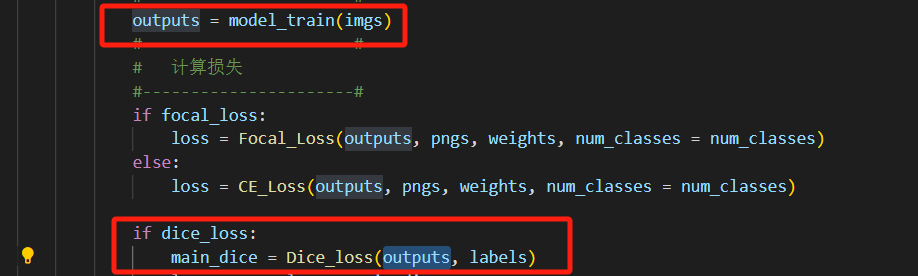
参考：

• F-score 和 Dice Loss
• https://github.com/bubbliiiing/deeplabv3-plus-pytorch/blob/main/utils/utils_metrics.py