信号类型——正交频分复用（OFDM）

? ? ? ? OFDM主要思想是将信道分成若干正交子信道，将高速数据信号转换成并行的低速子数据流，调制到在每个子信道上进行传输，正交信号可以通过在接收端采用相关技术来分开，这样可以减少子信道之间的相互干扰(ISI)?。每个子信道上的信号带宽小于信道的相关带宽，因此每个子信道上可以看成平坦性衰落，从而可以消除码间串扰，而且由于每个子信道的带宽仅仅是原信道带宽的一小部分，信道均衡变得相对容易。因此，OFDM信号实现关键之一是子信道（子载波）的确定。

1.1、子载波

假设OFDM系统存在K个子信道，每个子信道的中心频率（子载波）为：

$x_{k}\left ( t \right )=B_{k}\cos\left ( 2\pi f_{k}t+\varphi _{k} \right ),k=0,1,\cdots ,K-1$

其中 $B_{k},\varphi _{k}$ 分别表示第 $k$ 路子载波的幅度和相位，可由QPSK或QAM调制生成； $f_{k}$ 表示第 $k$ 路子载波的频率。N路子载波在一个OFDM符号时间内同时发射，因此OFDM信号在时域上表示为：

$e\left ( t \right )=\sum_{k=0}^{N-1}x_{k}\left ( t \right )=\sum_{k=0}^{N-1}B_{k}\cos\left ( 2\pi f_{k}t+\varphi _{k} \right )$

由于不同子信道的信号 $x_{k}\left ( t \right )$ 在时域上是混叠的，为了将其分离出来了，需要对每个子信道的被调制载波施加限制，使其满足正交性，即：

$\int_{0}^{T_{B}}\cos\left ( 2\pi f_{k}t+\varphi _{k} \right )\cos\left ( 2\pi f_{i}t+\varphi _{i} \right )dt=0$

其中 $T_{B}$ 为每个子信道码元持续时间，即OFDM符号时长。上式根据积化和差公式，可以看成 $f_{k}+f_{i}$ 和 $f_{k}-f_{i}$ 两个单频信号的积分，为了满足积分和为零， $f_{k}+f_{i}$ 和 $f_{k}-f_{i}$ 在一个符号时间 $T_{B}$ 内需要有整数个载波周期，即：

$\left (f_{k}+f_{i} \right )T_{B}=m,\left (f_{k}-f_{i} \right )T_{B}=n$

其中m,n均为整数， $\varphi _{k},\varphi _{i}$ 为任意值。因此子载波要求 $\Delta f_{min}=\left (f_{k}-f_{i} \right )_{min}=\frac{1}{T_{B}}$ 且 $f_{k}=\frac{k}{2T_{B}}$ 。

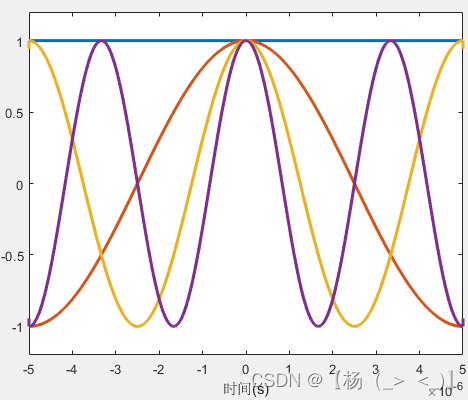
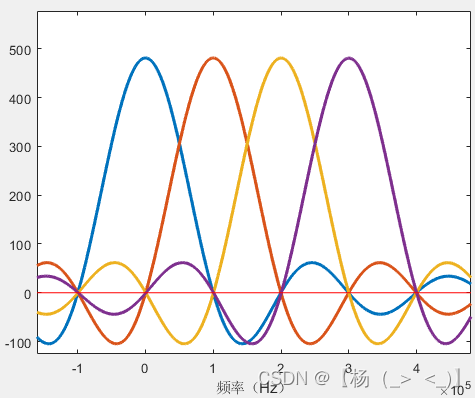
子载波时域波形? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?子载波频谱（实部）

? ? ? ? 每个子载波幅度以及初相一致，上图分别展示了各个子信道下信号的时域以及频域波形。从频域可以看出，在每个子载波频率处，FFT得到频谱幅度以及相位只与该子载波对应调制幅度以及相位有关，其他子载波的调制信息不影响该子载波频率上频谱的取值。而这正是子载波正交条件下OFDM信号的特点，可以利用这一性质通过FFT处理从OFDM时域信号解调处调制信息。

? ? ? ?下图分别展示了不同子信道数下信号频谱（每个子信道调制信息一致，子信道从-K/2到K/2-1）。可以看出子信道越多，信号频谱越趋于矩形。

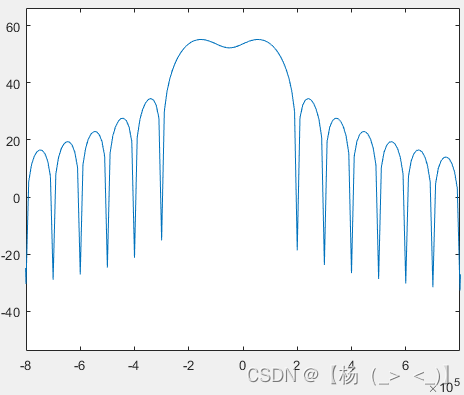
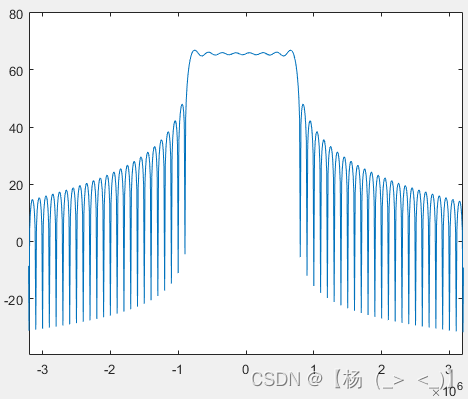
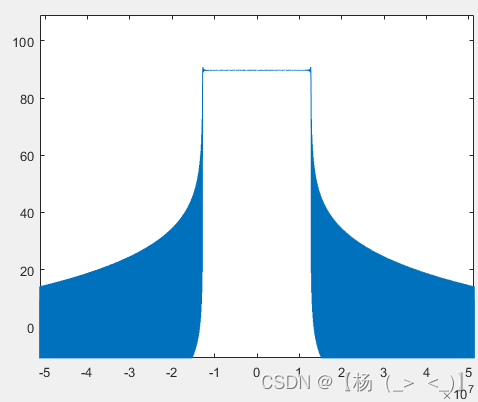
子载波数4? ? ? ? ? ? ? ? ? ? ? ? ? 子载波数16? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?子载波数256?

1.2、OFDM的快速实现

? ? ? ?OFDM时域信号可以认为是多个单频信号的叠加，因此可以由多个频率源单独生成并调制信号后混叠产生，但是这对频率源稳定度有着极高要求（受子载波正交条件限制），实际很难实现，此外如果基于数字化的信号产生方式生成每个子信道的数据，然后叠加生成最终OFDM信号会导致数据量随着子信道数量增加而迅速增加。而基于IFFT的OFDM信号生成方式很好的解决上述问题。下面简单介绍原理，OFDM连续信号在复数形式中可以表达为：

$e\left ( t \right )=\sum_{k=0}^{K-1}s\left (k \right )e^{2\pi f_{k}t}$

其中 $s\left (k \right )$ 为调制信号（如QPSK、QAM调制信号）。信号表现形式类似IFFT变换，为了构造IFFT形式， $f_{k}=\frac{k}{T_B}$ ，并对上式信号进行 $\frac{T_B}{K}$ 间隔的采样，则离散的OFDM信号为：

$e\left ( l \right )=\sum_{k=0}^{K-1}s\left (k \right )e^{2\pi \frac{k}{T_{B}}\frac{lT_{B}}{K}}=\sum_{k=0}^{K-1}s\left (k \right )e^{2\pi \frac{kl}{K}}$

因此OFDM离散信号可以通过K点调制信息 $S=\left [s\left (0 \right ),s\left (1 \right ), \cdots ,s\left (K-1 \right ) \right ]^{T}$ 的IFFT变化得到OFDM离散信号。同样的，当已知OFDM信号的采样值 $S=\left [e\left (0 \right ),e\left (1 \right ), \cdots ,e\left (K-1 \right ) \right ]^{T}$ ，可以通过FFT得到调制信号 $S$ 。

? ? ? ?考虑到实际能够发射的信号是模拟信号，需要由通过DAC将OFDM离散信号 $e\left ( l \right )$ 转变为OFDM连续信号 $e\left ( t \right )$ 。为了抑制带外信号能量，在对信号进行DAC处理过程中也会进行成型滤波处理。

? ? ? ?考虑到实际传输信号为实信号，这里有两种方案。

? ? ? ? 一种是基于IQ调制技术实现复信号 $e\left ( t \right )$ 的发射，发射信号表示为：

$s\left ( t \right )=a\left ( t \right )\cos(2\pi f_{c}t)-b(t)\sin(2\pi f_{c}t)$

其中 $e\left ( t \right )=a\left ( t \right )+jb(t)$ ， $f_{c}$ 为发射载频。

? ? ? ?另一种是利用调制信号，构造新的用于生成最终OFDM信号的调制信号，构造原理是基于实信号的频谱复共轭对称特点。新的调制信息 $S'=\left [s'\left (0 \right ),s'\left (1 \right ), \cdots ,s'\left (2K-1 \right ) \right ]^{T}$ 长度为原来两倍，且满足：

$s'(2K-k-1)=s(k),k=1,2,\cdots ,K-1$

$s'(2K-k-1)=s(2K-k-1),k=K,K+1,\cdots ,2K-2$

$s'(0)=Re(s(0))$

$s'(2K-1)=Im(s(0))$

由此构造的调制信息 $S'$ 复共轭对称，因此IFFT得到OFDM离散信号为实信号，不过这种方式会浪费一半的子信道资源。

? ? ? ?考虑到实际接收信号会存在多径效应，与单载波传输相比，虽然OFDM增加了每个子信道的码元时长，但这种因为多径引起的码间串扰仍然存在。为了进一步消除多径引起的码间串扰（ISI），在每个OFDM符号之间会设置保护间隔，同时为了保证不同子载波在经过多径效应之后仍能保证正交性，保护间隔内由OFDM尾部信号填充，称为循环前缀。

1.3、问题

? ? ? ? ?对相位噪声和载波频偏十分敏感。任何一点小的载波频偏都会破坏子载波之间的正交性，引起子信道干扰ICI。同样，相位噪声也会导致码元星座点的旋转、扩散，形成ISI。而单载波系统就没有这个问题，相位噪声和载波频偏仅仅是降低了接收到的信噪比SNR，而不会引起互相之间的干扰。信号峰均比过大，将会增加A/D和D/A的复杂性，而且会降低射频功率放大器的效率。同时，在发射端，放大器的最大输出功率就限制了信号的峰值，这会在OFDM频段内和相邻频段之间产生干扰。

二、OFDM调制与解调

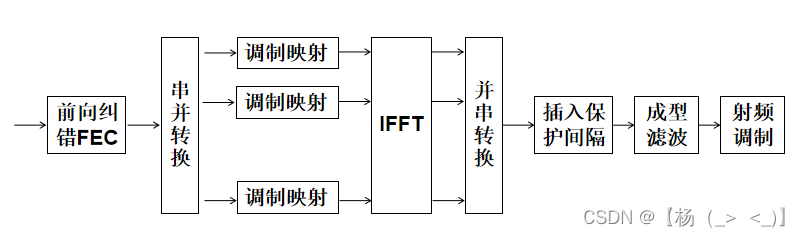
OFDM调制原理图

? ? ? ?在发射端，首先对比特流进行QAM或QPSK调制，然后依次经过串并转换和IFFT变换，再将并行数据转化为串行数据，加上保护间隔（又称“循环前缀”），形成OFDM码元。在组帧时，须加入同步序列和信道估计序列，以便接收端进行突发检测、同步和信道估计，最后输出正交的基带信号。

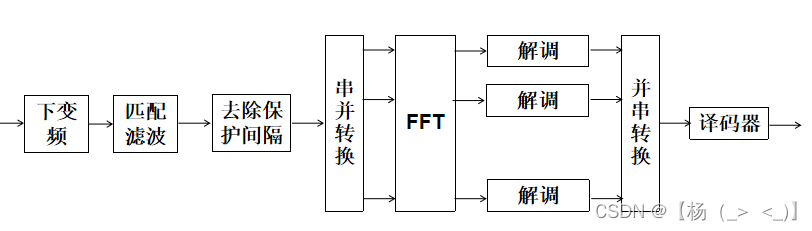
OFDM解调原理图

? ? ? ?当接收机检测到信号到达时，首先进行同步和信道估计。当完成时间同步、小数倍频偏估计和纠正后，经过FFT变换，进行整数倍频偏估计和纠正，此时得到的数据是QAM或QPSK的已调数据。对该数据进行相应的解调，就可得到比特流。

? ? ? ?实际非理想传输条件以及非理想接收机状态的影响下，OFDM的解调首先需要考虑OFDM信号的同步问题，包括采样时钟同步（采样时钟晶振不稳定导致的）、码元/OFDM符号同步（收发机相互分离导致的）以及载频同步（多普勒效应等导致的），同步的目的主要为了确定OFDM解调时FFT运算的截取窗口位置；然后是基于导频或训练序列等先验证信息的进行信道的估计。这里不详细展开，感性兴趣的可以参考文献。

三、仿真

3.1、不同导频模式

块状导频

? ? ? ?参数设置，符号速率100kHz，QPSK调制映射，256载波位，块状导频，时间间隔4，保护间隔位为FFT点数的四分之一，根升余弦成型滤波器，滚降系数0.3，符号数6。

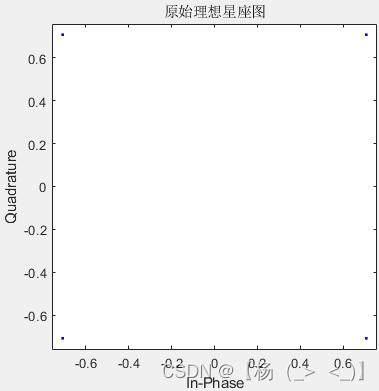
（a）QPSK调制星座图? ? ? ? ? ? ? ? ? ? ?（b）导频图案

上图为OFDM调制前QPSK调制星座图，以及OFDM插入的导频图案（导频的位置分布）。

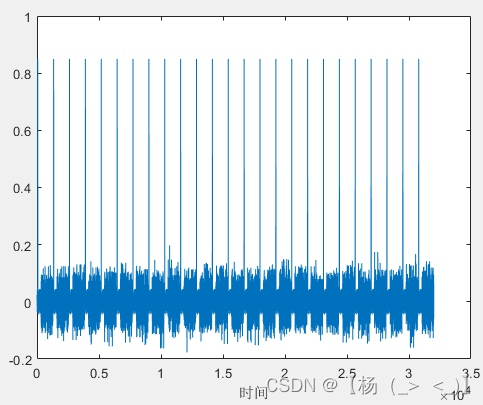
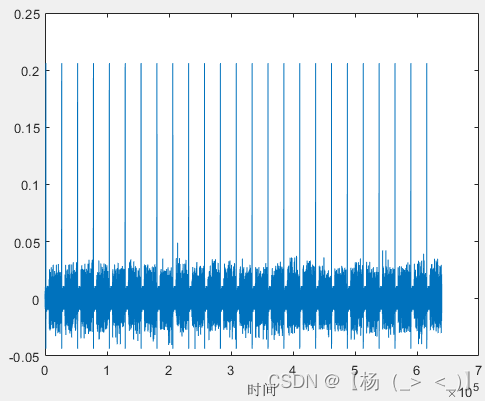
（a）成型滤波前时域信号 ?????????（b）成型滤波后时域信号

? ? ? ?上图为块状导频OFDM信号成型滤波前后时域信号，下图分别为信号频谱以及OFDM解调后的星座图

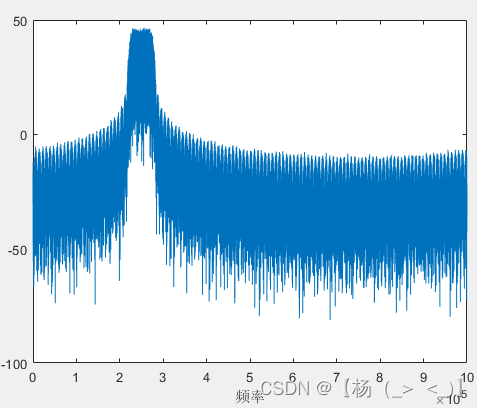
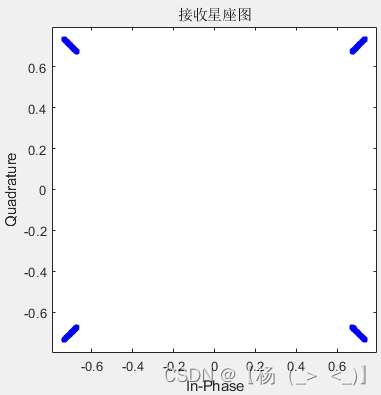
信号频谱以及星座图

梳状导频

? ? ? ? ? ? ?参数设置，符号速率100kHz，QPSK调制映射，256载波位，其中180数据载波位，梳状导频，载频间隔4，保护间隔位为FFT点数的四分之一，根升余弦成型滤波器，滚降系数0.3，符号数6。

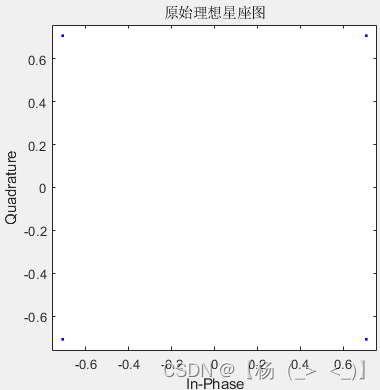
（a）QPSK调制星座图? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （b）导频图案

上图为OFDM调制前QPSK调制星座图，以及OFDM插入的导频图案（导频的位置分布）。

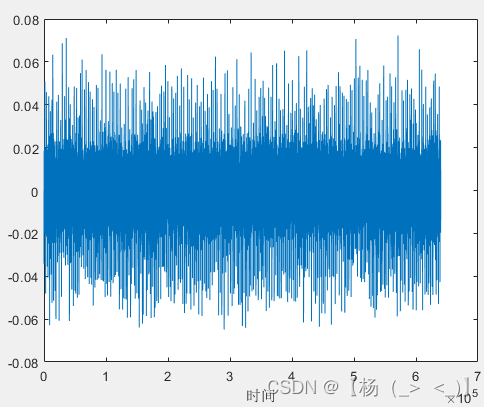
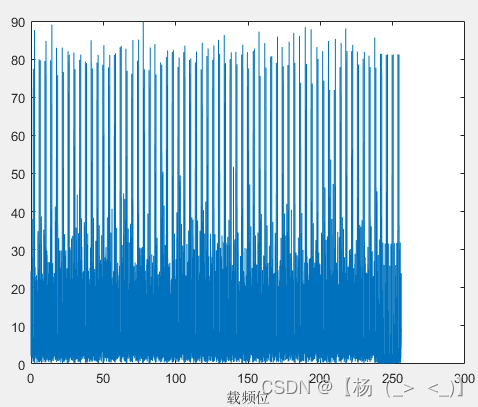
（a）成型滤波后时域信号 ?????????（b）成型滤波后频域信号

? ? ? ?上图为梳状导频OFDM信号成型滤波前后时域信号，下图分别为信号频谱以及OFDM解调后的星座图

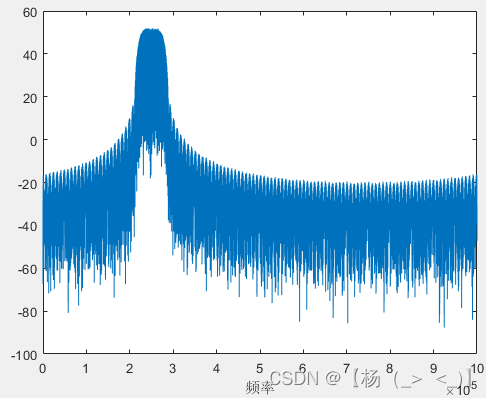
信号频谱以及星座图

3.2、成型滤波的影响

滤波器长度6（滚降系数0.05，0.3，0.8）

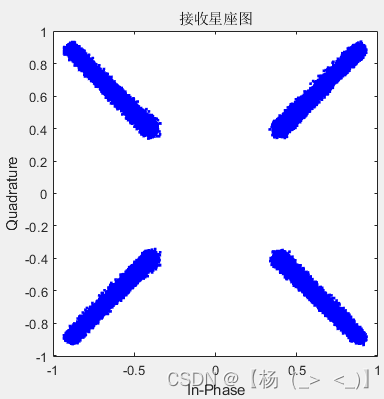
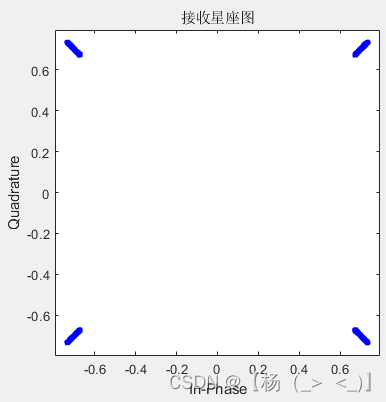
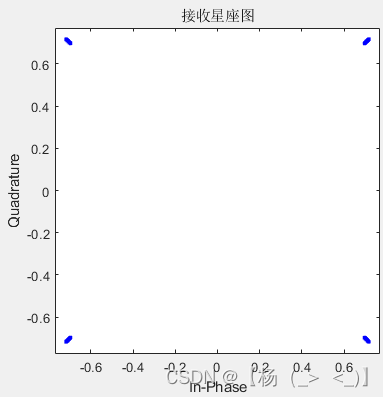
滤波器长度16（滚降系数0.05，0.3，0.8）

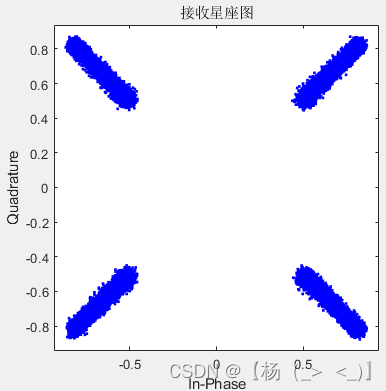
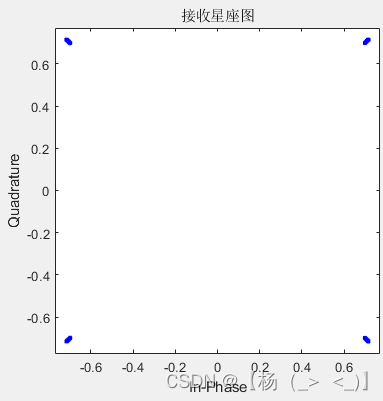
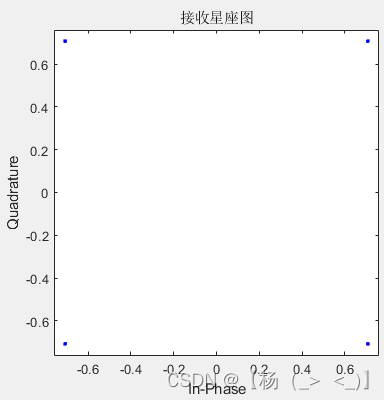
参考文献

1、樊昌信曹丽娜《通信原理》第7版

2、邝育军. OFDM无线传输系统中定时同步和信道估计的研究[D]. 北京:北京邮电大学,2003.

总结

? ? ? ?本文重点介绍OFDM调制与解调原理，并结合仿真分析OFDM信号传输过程。有问题也欢迎评论区留言。转载请附链接【杨（_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主。

文章来源:https://blog.csdn.net/yjh_2019/article/details/134500047
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！