EM（Expectation-Maximum）算法
EM算法
简介
EM算法的核心分为两步
- E步（Expection-Step）
- M步（Maximization-Step）
因为在最大化过程中存在两个参量 r , θ r,\theta r,θ，其中若知道 r r r，则知道 θ \theta θ；若知道 θ \theta θ，则知道 r r r。且两个量未存在明显的关系，但又互相依存可以采用EM算法
其中主要思想为：
- 首先随机初始化参数 r r r
- 然后求的在参数 r r r下按照极大似然估计求得参数 θ \theta θ
- 然后根据参数 θ \theta θ按照极大似然估计求得参数 r r r
- 循环至收敛
算法示例
如下图所示存在A，B两种硬币，其中抛出正反面的概率未知，其中H表示正面，F表示反面
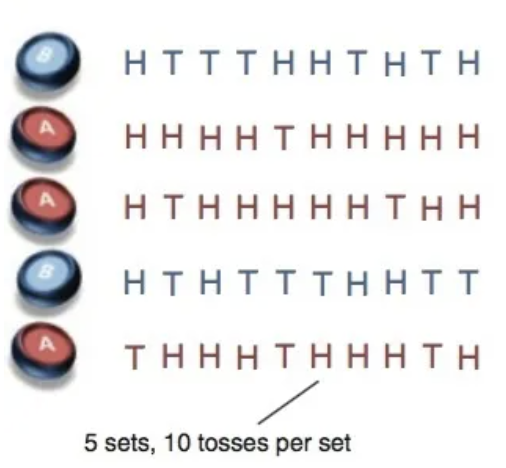
根据统计可得
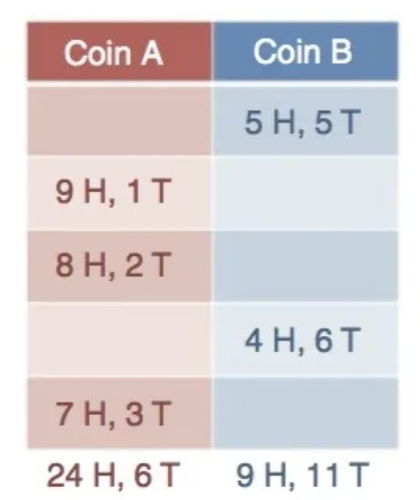
可得
P
(
H
∣
X
=
A
)
=
24
24
+
6
=
0.8
P
(
H
∣
X
=
B
)
=
9
9
+
11
=
0.45
P(H|X=A)=\frac{24}{24+6}=0.8\\ P(H|X=B)=\frac{9}{9+11}=0.45
P(H∣X=A)=24+624?=0.8P(H∣X=B)=9+119?=0.45
若更改条件，不知道此时抛出是哪一枚硬币，只知道抛出的结果，即
首先初始化，设
P
(
H
∣
X
=
A
)
=
0.6
P
(
H
∣
X
=
B
)
=
0.5
P(H|X=A)=0.6\\ P(H|X=B)=0.5
P(H∣X=A)=0.6P(H∣X=B)=0.5
若当抛出的第一枚硬币为A时
此时的出现该情况的概率为 P 1 ( A ) = 0. 6 5 ? ( 1 ? 0.6 ) 5 = 0.0007962624 P_1(A)=0.6^5*(1-0.6)^5=0.0007962624 P1?(A)=0.65?(1?0.6)5=0.0007962624
若当抛出的第一枚硬币为B时
此时的出现该情况的概率为 P 1 ( B ) = 0. 5 5 ? ( 1 ? 0.5 ) 5 = 0.0009765625 P_1(B)=0.5^5*(1-0.5)^5=0.0009765625 P1?(B)=0.55?(1?0.5)5=0.0009765625
其中
P
1
(
A
)
=
P
1
(
A
)
P
1
(
A
)
+
P
1
(
B
)
≈
0.45
P
1
(
B
)
=
P
1
(
B
)
P
1
(
A
)
+
P
1
(
B
)
≈
0.55
P^1(A)=\frac{P_1(A)}{P_1(A)+P_1(B)}\approx0.45\\ P^1(B)=\frac{P_1(B)}{P_1(A)+P_1(B)}\approx0.55
P1(A)=P1?(A)+P1?(B)P1?(A)?≈0.45P1(B)=P1?(A)+P1?(B)P1?(B)?≈0.55
同理可得
P
2
(
A
)
≈
0.80
,
P
2
(
B
)
≈
0.20
P
3
(
A
)
≈
0.73
,
P
3
(
B
)
≈
0.27
P
4
(
A
)
≈
0.35
,
P
4
(
B
)
≈
0.65
P
5
(
A
)
≈
0.65
,
P
5
(
B
)
≈
0.35
P^2(A)\approx0.80,P^2(B)\approx0.20\\ P^3(A)\approx0.73,P^3(B)\approx0.27\\ P^4(A)\approx0.35,P^4(B)\approx0.65\\ P^5(A)\approx0.65,P^5(B)\approx0.35
P2(A)≈0.80,P2(B)≈0.20P3(A)≈0.73,P3(B)≈0.27P4(A)≈0.35,P4(B)≈0.65P5(A)≈0.65,P5(B)≈0.35
设第2，3，5轮抛出的为硬币A，第1，4轮抛出的为硬币B，可得
P
(
H
∣
X
=
A
)
=
9
+
8
+
7
30
=
24
30
=
0.8
P
(
H
∣
X
=
B
)
=
5
+
4
20
=
9
20
=
0.45
P(H|X=A)=\frac{9+8+7}{30}=\frac{24}{30}=0.8\\ P(H|X=B)=\frac{5+4}{20}=\frac{9}{20}=0.45
P(H∣X=A)=309+8+7?=3024?=0.8P(H∣X=B)=205+4?=209?=0.45
由此循环直至收敛
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！