八大算法排序@选择排序

选择排序

概念

??选择排序（Selection Sort）是一种简单直观的排序算法。基本思想是在未排序的序列中找到最小（或最大）元素，然后将其放到序列的起始位置，再从剩余未排序的序列中找到最小（或最大）元素，放到已排序序列的末尾。以此类推，直到整个序列排序完成。

算法思想

主要思路就是找出未排序的序列中的最小/最大的元素，置换到有序序列的尾巴上，实现有序序列的升序/降序效果。当有序序列的长度等于数组长度时，数组排序完成。我们拿实现升序的选择排序来进行模拟演变。

示例

如下是数组arr1 = { 6 , 4 , 3 , 9 , 2 , 1 , 5 , 7 , 8 }初始状态下的图文演示：

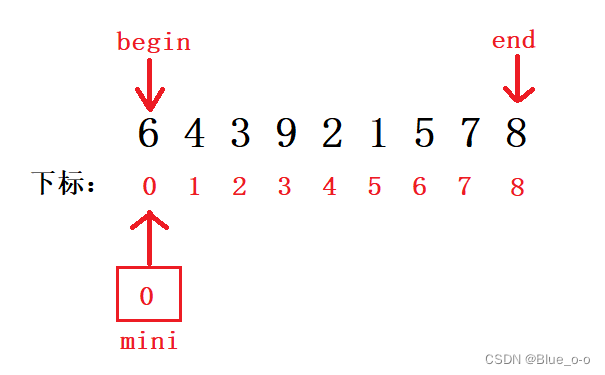
其中，变量begin、end是数组的第一个和最后一个元素的下标，变量mini用来存储未排序数组的最小元素的下标。

步骤1

第一次，在为排序的数组序列中，找到序列中最小的元素的下标：

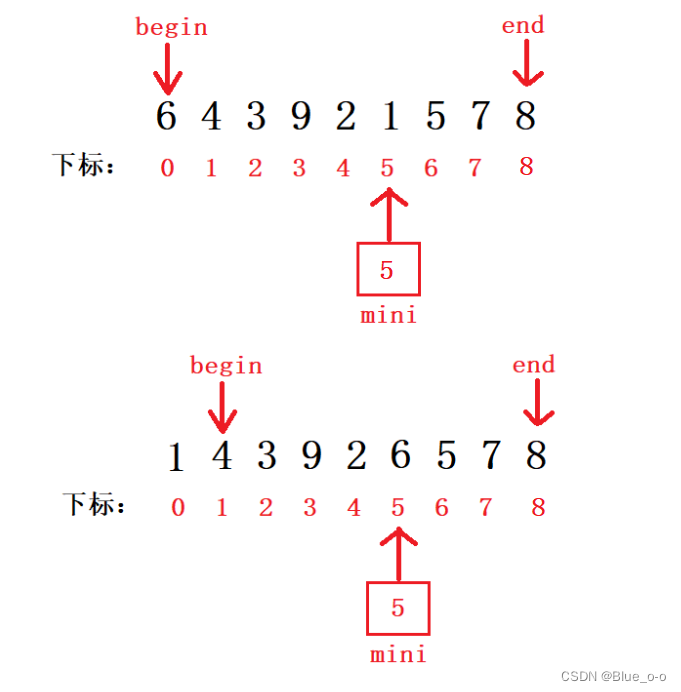
如图，找到最小的元素1，将元素1的下标5存到mini变量中，然后将arr1[begin] 和 arr1[mini] 两个元素位置互换，begin再加1，因为begin是未排序的序列的第一个元素的下标值。

步骤2

第二次，继续在为排序的数组序列中，找到序列中最小的元素的下标：

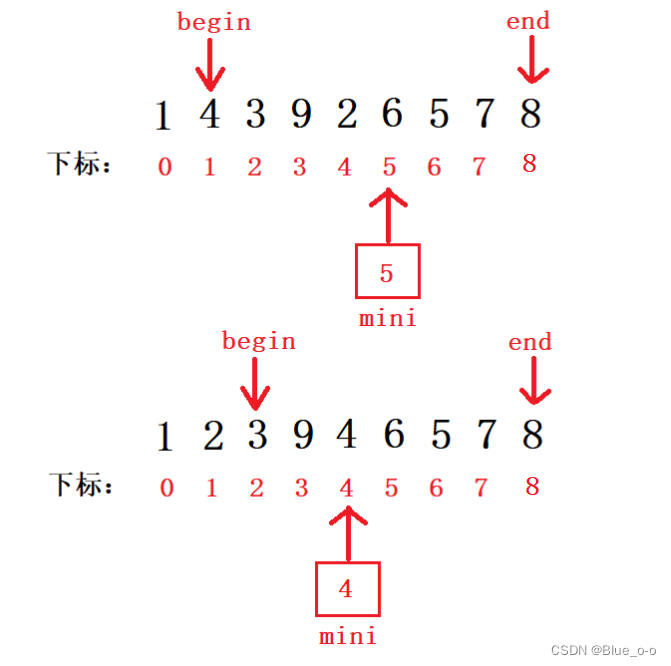
在未排序的数组中最小的元素2的下标为4，存到mini变量中，然后将arr1[begin] 和 arr1[mini] 两个元素位置互换，begin再加1。

步骤…n

重复以上的步骤，具体的我就不多加演示，下面是最后一次的排序演示图：

最后一步

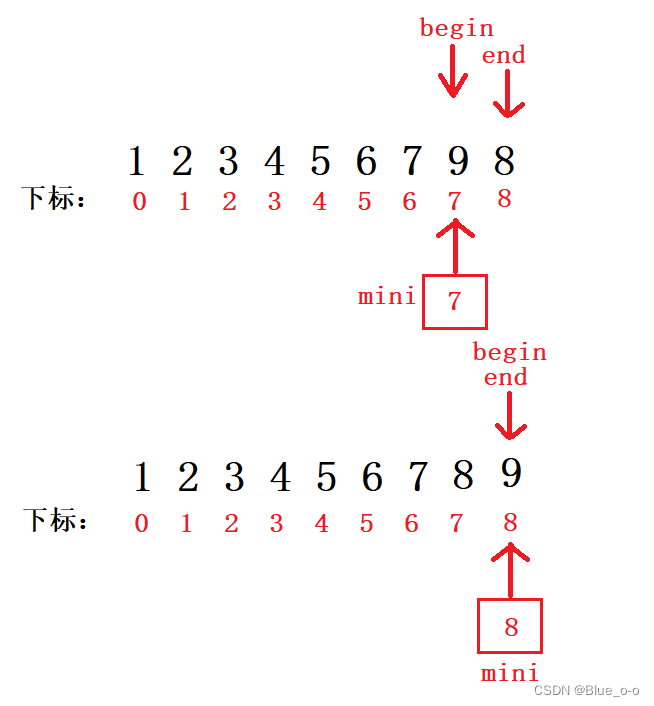
当begin和end 相等时，此时整个数组已经有序，已经排序成升序的效果。

以上便是关于选择排序的相关图形流程，下面结合图形流程，编写代码。

代码实现

选择排序的步骤如下：
初始化： 将序列分为两部分，一部分为已排序的部分，一部分为未排序的部分。初始时，已排序部分为空。
步骤2：在未排序部分中找到最小元素： 遍历未排序部分，找到最小的元素。
步骤3：交换： 将找到的最小元素与未排序部分的第一个元素交换位置，将其加入到已排序部分。
重复： 重复步骤2和步骤3，直到未排序部分为空。

代码实现：

// 交换函数
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}


//选择排序
void SelectSort(int* a, int n)
{
	assert(a);

	int begin = 0;		// 有序数组的最后一个元素的下标
	int end = n - 1;	// 数组最后一个元素的下标

	int mini = begin;
	// 当begin==end时，整个数组已经排序完，退出循环。否则一直循环进行排序
	while (begin < end)
	{
		// 在未排序的序列里找出最小的元素的下标，存到变量mini中
		for (int i = begin + 1; i <= end; i++)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
		// 将序列中最小的数组置换到前面，实现升序的排序效果
		Swap(&a[begin], &a[mini]);		//小的放在最前面
		begin++;  // 有序的数组加1，最后一个元素的下标随之加1
	}
	// 实现数组的升序排序。
}

以上，便是选择排序的实现代码，在此基础上，我们还可以进一步的改进。原先是在未排序的序列中找出最小/最大的元素，置换到排好序的序列的末尾中，一次只能排一个数。
现在改进点：每次排两个数，即在未排序的序列中，找出最大和最小的元素下标，分别存到变量中。然后将最大的排到最后面，最小的排到最前面（升序）。然后begin加1，end减1，接着做重复的动作，每次排好两个数。如下图：

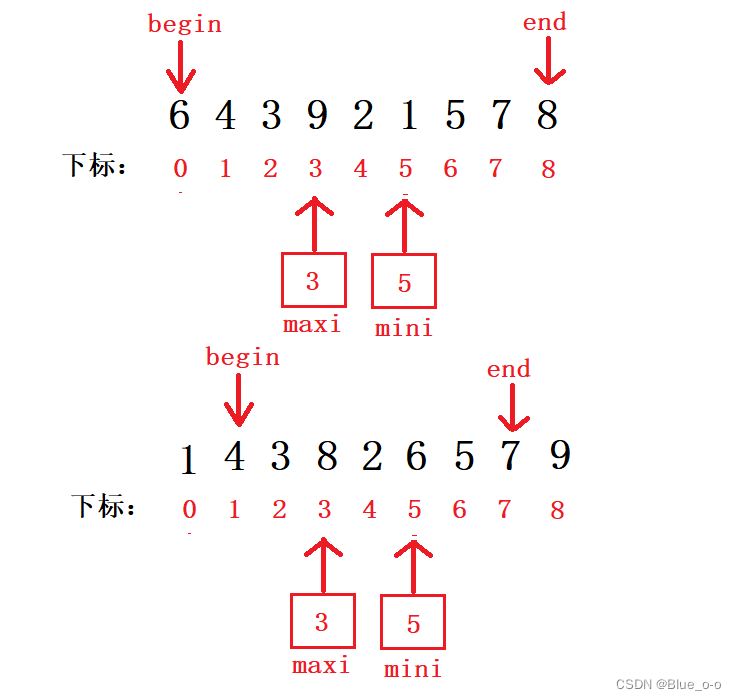
代码实现如下：

// 交换函数
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}


//选择排序
void SelectSort(int* a, int n)
{
	assert(a);

	int begin = 0;
	int end = n - 1;
	int maxi = begin;
	int mini = begin;

	while (begin < end)
	{
		for (int i = begin + 1; i <= end; i++)
		{
			if (a[i] > a[maxi])
			{
				maxi = i;
			}

			if (a[i] < a[mini])
			{
				mini = i;
			}
		}


		Swap(&a[end], &a[maxi]);		//大的放在最后面
		if (mini == end)
		{
			mini = maxi;
		}
		Swap(&a[begin], &a[mini]);		//小的放在最前面
		begin++;
		end--;
		maxi = mini = begin;
	}

}

需要注意：边界的问题。

时间复杂度

O(N^2)。
不管是一次只排一个数的选择排序，还是一次排两个数的选择排序，时间复杂度都是O(N^2)，当然后者肯定比前者效率更高一点，为 O(N^2 / 2)，但是时间复杂度的计算是不计入系数的。所以两者的时间复杂度都是O(N^2)。

空间复杂度

O(1)。
在原数组上改动，没有用到多余的空间，所以空间复杂度为O(1)。

特性总结

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定