动态规划高频问题

关卡名	掌握动态规划如何解题的	我会了??
内容	1.最少硬币数问题	??
	2.最长连续递增子序列问题	??
	3.最长递增子序列问题	??
	4.最少完全平方数问题	??
	5.再论青蛙跳问题	??
	6.解法方法	??
	7.路径中的障碍物问题	??
	8.滚动数组处理技巧	??

本文我们就来盘点那些常见的动态规划问题，本章除了最后两个题，其他都使用一维数组就可以了，因此我们每道题都要先明白，这个基表arr的含义是什么，如何更新的：
本章，我们首先通过详细的过程一步步来分析最少硬币数的问题，仔细观察每一步都是在做什么。代码如何从比较low的样子优化到比较合理。从2.2开始我们的讲解会更加精简。

1 最少硬币数 ?

LeetCode322.给你一个整数数组 coins ，表示不同面额的硬币，以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。

示例1：

输入：coins = [1, 2, 5], amount = 11

输出：3

解释：11 = 5 + 5 + 1

示例2：

输入：coins = [2,5, 7], amount = 27

输出：3

解释：21 = 7 + 7 + 7

画图分析
这个题，其实使用上一章的回溯法也能做，问题就是效率太低了。假如coins = [2,5, 7], amount = 27，在求解过程中，每个位置都可以从{2,5,7}中选择 ，因此可以逐步将所有情况枚举出来，然后再找到要求的最少硬币数，图示如下：?

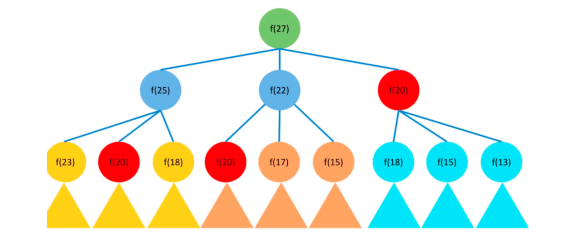
通过上面的图，我们发现f[20]等已经存在多次重复计算了，这就是存在大量的重复计算问题，效率低，所以可以使用动态规划来优化。
另外貌似贪心也可以，直觉告诉我们尽量使用大的，例如假如要求的是27，此时应该先连续用7 + 7+7=21，最后的6没法了就用2，则就是3个7加3个2，一共6个，但我们可以这么做7+5+5+5+5=27 ，使用5枚硬币就够了，这就是贪心的思路，但对于本题就是错误的。
使用动态规划能同时满足效率和准确性的最佳，自然地，我们设状态f(x)=最少用f(x)枚硬币能拼出x。对应到上面基表就表示最少用arr[i]个硬币能表示出i来。我们先看上面给的示例1的情况：

上面图中，索引表示的是amount，而每个位置表示就是最少需要arr[i]个硬币就能拼出来。但是有些场景下可能不能将所有位置都能拼接出来的，例如示例2中的：

?我们注意上面有些位是放的是M，表示的就是不能拼出来的意思。接下来我们就以coins={2,5,7}来详细分析如何一步步实现DP。

第一步：确定状态和子问题

什么是状态？前面介绍过，解动态规划的时候需要一个数组，状态就是这个数组的每个元素f[i]表示什么。
DP从思想上看仍然是递归，我们要找到将问题范围缩小的递推表达式，也就是状态转移方程。对于大部分DP的题目，先看最后一步的情况更容易分析出来，所以我们的武功心法第一条是从后向前找递归。
这里的最后一步就是：虽然我们不知道最优策略是什么，但是我知道最后得到最优策略一定是K枚硬币，a1，a2，...ak，而且面值加起来是27，而除掉ak这枚硬币，前面硬币加起来就是27-ak。此时我们得到:

这里貌似我们还不知道ak是多少？但是那一枚一定是2，5，7中的一个。

• 如果ak是2，那么f(27)应该是f(27-2)+1,加上最后这一枚硬币2。 f(25)+1
• 如果ak是5，那么f(27)应该是f(27-5)+1,加上最后这一枚硬币5。 f(22)+1
• 如果ak是7，那么f(27)应该是f(27-7)+1,加上最后这一枚硬币7。 f(20)+1

除此之外，没有其他可能了。那我们最后到底要使用哪一个呢？很简单，就是选上面三种情况最小的那个，也就是：
f(n):n是我们是要拼的数，这里f(n) 表示拼成n所需的最少硬币数
f(27)= min{ f(25)+1,f(22)+1,f(20)+1}
f(27)= min{ f(25),f(22),f(20)}+1
f(n)=min{f(n-2),f(n-5),f(n-7)}+1
f(27)=min{f(27-2)+1,f(27-5)+1,f(27-7)+1}
在上面的过程中，我们不关心前面的K-1枚硬币是怎么拼出27-ak的，前K-1步可能有一种拼法，也可能有100种，甚至我们也没确定ak和k是啥，但是能确定的是前面一定拼出了27-ak，并且此时使用的硬币总数m=k-1枚一定是最少的，否则就不是最优策略,这里本题的一个核心， 也是不太好理解的地方。
到此，要处理的子问题就是”最少用多少枚硬币可以拼出27-ak，而原始问题是"最少用多少枚硬币拼出27"。这样，我们就将原问题转化成了一个子问题，而且规模更小27-ak。
而至于最后一个ak，我们就是简单枚举了一下，要么是2，要么是5，要么是7，这就是局部枚举。而且到现在为止，我们也不知道到底用哪一个，唯一能确定的就是最后一个肯定是从2,5,7中选了一个，所以只是得到这样一个壳子：
f(27)=min{f(25)+1,f(22)+1,f(20)+1}
那接下来要怎么办呢？很简单，就是根据递归的思想再去算f(25)、f(22)和f(20)，例如计算f(20)就是:
f(20)=min{f(18)+1,f(15)+1,f(13)+1}
到这里仍然是不知道结果的，那就继续算，例如计算f(13)就是：
f(13)=min{f(11)+1,f(8)+1,f(6)+1}
到这里还是不知道结果，那就继续算，例如计算f(6)就是：
f(6)=min{f(4)+1,f(1)+1,f(-1)+1}
到这里很明显就非常容易计算了。
通过上面的例子，我们终于明白为什么找递推要从右向左，而计算的时候要从左向后了。
当然这里很明显f(-1)不符合要求的，那就设置为正无穷就行了。f(1)=也是正无穷，而f(4)=2，所以f(6)=2+1=3，然后继续计算最大的，最后就得到我们想要的结果。?

第二步：确定状态转移方程?

子问题确定之后，状态转移方程就很容易了，为了简化定义，我们设状态为f(x)=最少使用多少枚硬币拼出X。根据上面的分析，这里的ak，只能是2，5或者7。而我们要求的最少硬币数，就是求下面三个的最小值：

这个就是状态转移方程，在上一步我们已经分析出来了。
再往后，就是采用一样的套路将f(25)、f(22)和f(20)一起交给后续递归过程继续算。

第三步：确定初始条件和边界?

很明显，本题的初始条件是: f[0]=0
对于上面的公式，有两个问题如果x-2，x-5，x-7，小于0怎么办？如果不能拼出x，就定义f[x]为正无穷，例如f[-1]=f[-2]=...=正无穷，表示拼不出1来。思考一下，这里为什么不能初始化为0？
当然这里有一点要注意，我们上面不可达用的是M，而不是Integer.MAX，因为这样的公式溢出了：
f(6)=min{2,Integer.MAX+1,Integer.MAX+1,}
我们可以使用amount来代替Integer.MAX

第四步：按顺序计算

开始执行上面的f[x]计算公式，f[x]=min{f[x-2]+1,f[x-5]+1,f[x-7]+1}
虽然推导我们是从后向前 ，但是计算我们一般是从前向后的，在第一步中已经解释过，我们的计算过程如下：
初始条件：f[0]=0
然后计算f[1],f[2],...f[27]
这样的好处是计算f[x]的时候，f[x-2],f[x-5],f[x-7]都已经计算到结果了，因此效率更高。
执行的结构图如下（f[x]表示最少用几个硬币和拼出X，无穷表示无法拼出）：

现在请你思考一下这里的数字是怎么逐步计算出来的。这里其实每一步计算都是尝试3种硬币，一共27步，但是与递归相比，没有任何重复计算。因此算法时间复杂度为27*3。而递归的时间复杂度远远大于该数。
在这里每一步都尝试三种硬币，一共27步，对应的也就是一维数组的大小。
可以看到，与递归相比没有任何重复计算，因此效率更高。

第五步：代码实现?

经过上面的分析之后，我们接下来就要实现上面的逻辑。根据上面f[x]的公式，我们可以写出第一版的代码：

//不能执行,仅仅做学习思考
int coinChange(int[] coins, int amount) {
    int max = amount + 1; Interge.MAX
    int[] dp = new int[amount + 1];
    Arrays.fill(dp, max);
    dp[0] = 0;
    for (int i = 1; i <= amount; i++) {
        if(check(i,coins)){
            dp[i] = min(dp[i], dp[i - coins[0]] + 1,dp[i - coins[1]] + 1,dp[i - coins[2]] + 1);
        }   
    }
    return dp[amount] > amount ? -1 : dp[amount];
}

boolean check(int i,int []coins){
    // 这里要保证if里使用的i - coins[j]等大于零
    // 这里还要保证不越界，写起来比较复杂 ，我们理解功能即可 
}

上面的min()方法我们暂时不实现，反正是从中找最小的那个。但这个代码不太优雅，dp的计算太长了，我们可以通过下面的方式来调整一下：

//不能执行,仅仅做学习思考
public int coinChange(int[] coins, int amount) {
    int max = amount + 1;
    int[] dp = new int[amount + 1];
    Arrays.fill(dp, max);
    dp[0] = 0;
    for (int i = 1; i <= amount; i++) {
        if(check(i,coins) ){//简写
            dp[i] = min(dp[i], dp[i - coins[0]] + 1);
            dp[i] = min(dp[i], dp[i - coins[1]] + 1);
            dp[i] = min(dp[i], dp[i - coins[2]] + 1);
        }   
    }
    return dp[amount] > amount ? -1 : dp[amount];
}
boolean check(int i,int []coins){
    // 这里要保证if里使用的i - coins[j]等大于零
    // 这里还要保证不越界，写起来比较复杂 ，我们理解功能即可 
}

这样我们就可以通过三次计算dp分别来处理coins[]数组的情况。但是这么写仍然不好，如果coins[]数组比较大，if判断就会非常长。怎么办呢？好办，加个循环来解决。
最终代码如下：?

public static int coinChange(int[] coins, int M) {
    int max = M + 1;
    int[] dp = new int[M + 1];
    Arrays.fill(dp, max);
    dp[0] = 0;
    for (int i = 1; i <= M; i++) {
        for (int j = 0; j < coins.length; j++) {
            if (coins[j] <= i) {
                dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
            }
        }
    }
    return dp[M] > M ? -1 : dp[M];
}

这就是本题最终的实现方法。
这里虽然是递归，但是是通过循环+数组来实现的，这就是为了消除冗余加速计算。?

总结
我们现在来总结一下求最值型DP的步骤：
1.确定状态和子问题，从最后一步开始（最优策略中使用的最后一枚硬币ak）推导f(n)与子问题之间的关系，然后将其化成子问题(最少的硬币拼出更小的面值27-ak)。
2.通过状态，我们可以得到状态转移方程：f[x]=min{f[x-2]+1,f[x-5]+1,f[x-7]+1}
3.处理初始条件和边界情况。f[0]=0,其他的如果不能拼出来就标记为f[X]=正无穷。
4.从小到大开始计算。这里就是从f[0]、f[1]、f[2]..向后计算。?

2 最长连续递增子序列?

LeetCode674.给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例1：

输入：nums = [1,3,5,4,7]

输出：3

解释：最长连续递增序列是 [1,3,5], 长度为3。

尽管 [1,3,5,7]也是升序的子序列, 但它不是连续的，因为5和7在原数组里被4隔开。

对于本题，不用动态规划也可以解决，例如我们前面介绍的《滑动窗口》就可以。如果使用动态规划的话，我们仍然先手动画一下，看看数组变成什么样子：

?很明显就是从前向后累计一下，如果不再是递增了，就将f[x]设置为1，然后继续向前走。
这种问题也称为序列型动态规划，给定一个序列或者网格，需要找到序列中某个/些子序列或者网格中的某条路径，要求满足某种性质最大/最小，求计数或者判断存在性问题。?

第一步：确定状态和子问题?

分析最后一步，对于最优策略，一定有最后一个元素a[j]。我们先考虑简单情况：

• 第一种情况：最优策略中最长连续上升子序列就是{a[j]}，答案是1。
• 第二种情况：子序列长度大于1，那么最优策略中a[j]前一个元素肯定是a[j-1]，这种情况一定是a[j-1]<a[j]的。

因为是最优策略，那么它选中的以a[j-1]结尾的连续上升子序列一定是最长的。
这里我们也得到了子问题：求以a[j-1]结尾的最长连续上升子序列，而本来是求以a[j]结尾的最长连续上升子序列。
状态：设f[j]=以a[j]结尾的最长连续上升子序列的长度。
则转移方程就是：

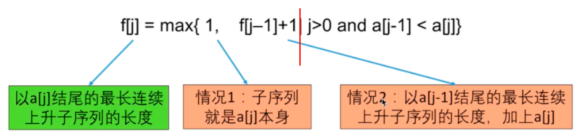
?注意上图中红色线前面的是表达式，后面是要满足的条件。
第二步：初始条件和边界

?情况2必须满足：j>0,即a[j]前面至少还有一个元素 并且a[j]>a[j-1]满足单调性。

第三步：按照顺序计算?

计算f[0]，f[1]，f[2]，...，f[n-1]
和硬币组合题不一样的是，最终答案不一定是f[n-1]，因为我们不知道最优策略中最后一个元素是哪个a[j]。所以答案是max{f[0]，f[1]，f[2]，...，f[n-1]}。?

public   int findLengthOfLCIS(int[] nums) {
    int[] dp = new int[nums.length];
    for (int i = 0; i < dp.length; i++) {
        dp[i] = 1;
    }
    int res = 1;
    for (int i = 0; i < nums.length - 1; i++) {
        if (nums[i + 1] > nums[i]) {
            dp[i + 1] = dp[i] + 1;
        }
        res = res > dp[i + 1] ? res : dp[i + 1];
    }
    return res;
}

3 最长递增子序列?

LeetCode300.给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例1：

输入：nums = [10,9,2,5,3,7,101,1]

输出：4

解释：最长递增子序列是 [2,3,7,101]，因此长度为4。

注意本题与上一题的区别就是没说一定是连续的，例如上面示例里2和7就不是连续的。本题该怎么做呢？我们还是先手动算一下看看：

我们看一下使用DP解决问题的方法：
第一步：确定状态
最后一步：对于最优的策略，一定有最后一个元素a[j]。
第一种情况：最优策略中最长上升子序列就是{a[j]}，答案是1。
第二种情况：子序列长度大于1，那么最优策略中a[j]前一个元素是a[i]，并且a[i]<a[j]?

?因为是最优策略，那么它选中的以a[i]结尾的上升子序列一定是最长的。
所以我们就得到子问题：因为不确定最优策略中a[j]前一个元素a[i]是哪一个，需要枚举每个i，求以a[j]结尾的最长上升子序列。化为子问题：i<j
状态：设f[j]=以a[j]结尾的最长上升子序列的长度

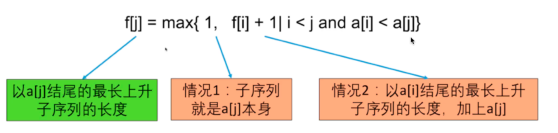
?第三步：初始条件和边界情况

情况2必须满足：①i>=0;② a[j]>a[i]，也就是满足单调性。

第四步：计算顺序

计算f[0]、f[1]、f[2]、....f[n-1]，答案就是这些数中最大的那个。
本题的时间复杂度为O(n^2)，空间复杂度O(n)。

public int lengthOfLIS(int[] A) {
    int n = A.length;
    if(n==0){
        return 0;
    }
    int i,j,res=0;
    int[] f = new int[n];
    for(int j=0;j<n;j++){
        f[j]=1;
        for(int i=0;i<j;i++){
            if(A[i]<A[j] && f[i]+1>f[j]){
                f[j]=f[i]+1;
            }
        }
        res=Math.max(res,f[j]);
    }
    return res;
}

?4 最少完全平方数

LeetCode279.给你一个整数 n ，返回和为n的完全平方数的最少数量。
完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例1：

输入：n = 12

输出：3

解释：12 = 4 + 4 + 4

示例2：

输入：n = 13

输出：2

解释：13 = 4 + 9

4 + 9

4 4 4 1

4 4 1 1 1 1 1 1

4 1 1 1 1 1 1 1 1 1

这个题如果通过暴力来算，一定会超时，我们还是考虑如何通过DP来做。首先我们看一下手动画一下看看数组的变化：?

?第一步：确定状态
先看序列的最后一步：关注最优策略中最后一个完全平方数j^2，那么最后策略中n-j^2也一定被划分成最少的完全平方数之和。因此需要知道n-j^2最少被分成几个完全平方数之和，而原问题是求n最少被分成接完全而平方数之和，这就是子问题。
根据子问题，我们可以确定状态了：设f[i]表示i最少被分成几个完全平方数之和。
第二步：确定状态转移方程
设f[i]表示i最少被分成几个完全平方数之和。

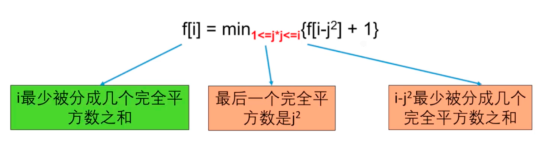
第三步：确定初始条件和边界条件
初始条件：0被分成0个完全平方数之和。f[0]=0。
然后依次计算f[1],...，f[N]
答案就是f[N]。?

public int numSquares(int n) {
    int[] f = new int[n+1];
    f[0]=0;
    for(int i=1;i<=n;i++){
        f[i] = Integer.MAX_VALUE;
        for(int j=1;j*j<=n;j++){
            if(f[i-j*j]+1<f[i]){
                f[i] = f[i-j*j]+1;
            }
        }
    }
    return f[n];
}

5 再论青蛙跳?

LeetCode55.跳跃游戏，给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位part置可以跳跃的最大长度。判断你是否能够到达最后一个下标。

示例1：

输入：nums = [2,3,1,1,4]

输出：true

解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例2：

输入：nums = [3,2,1,0,4]

输出：false

本题也是个典型的贪心问题，我们在贪心章节重点介绍过，我们现在从动态规划的角度考虑如何解决。

第一步：确定状态
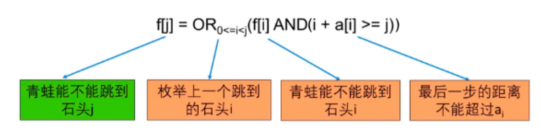
最后一步：如果青蛙能跳到最后一块石头n-1，我们考虑它跳的最后一步，这一步是从石头i跳过来的，i<n-1。
这需要同时满足两个条件：青蛙可以跳到石头i；最后一步不超过跳跃的最大距离：n-1-i<ai;
第二步：确定状态转移方程
那么我们需要知道青蛙能不能跳到石头i(i<n-1)，而原始问题是我们要求青蛙能不能跳到石头n-1，这就是子问题。
状态：设f[j]表示青蛙能不能跳到石头j(注意这里的f[j]是布尔类型)。因此可以确定状态转移方程了：

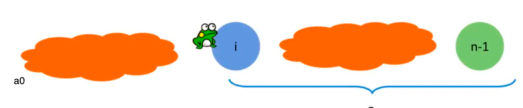
?这里使用or是因为只要存在一个就可以了。

第三步：确定初始条件和边界情况
设f[j]表示青蛙能不能跳到石头j。
初始条件：f[0]=true，因为青蛙一开始就在石头0。
第四步：按顺序计算
根据第二步中定义的f[j]和状态转移方程，并根据第三步的初始条件开始计算f[1],f[2],....f[n-1]。
f[n-1]就是我们最终想要的结果：?

public  boolean canJump(int[] A) {
    if(A==null || A.length==0){
        return false;
    }
    int n = A.length;
    boolean[] f = new boolean[n];
    f[0] = true;
    for(int j=1;i<n;j++){
        f[j]=false;
        for(int i=0;i<j;i++){
            if(f[i] && (A[i]+i>=j)){
                f[j]=true;
            }
        }
    }
    return f[n-1];
}

对于本题我们其实就是从i位置开始一直测试i+A[i]能不能到达A[n-1]，因此本质上就是一个两次循环，因此时间复杂度是O(N^2)，空间复杂度为O(N)。 ?

6 解码方法

LeetCode91.解码方法：一条包含字母 A-Z 的消息通过以下映射进行了 编码 ：

'A' -> "1"

'B' -> "2"

...

'Z' -> "26"

要解码已编码的消息，所有数字必须基于上述映射的方法，反向映射回字母（可能有多种方法）。例如，"11106" 可以映射为：
"AAJF" ，将消息分组为 (1 1 10 6)"KJF" ，将消息分组为 (11 10 6)注意，消息不能分组为 (1 11 06) ，因为 "06" 不能映射为 "F" ，这是由于 "6" 和 "06" 在映射中并不等价。
给你一个只含数字的非空字符串 s ，请计算并返回解码方法的总数 。?

示例1：

输入：s = "12"

输出：2

解释：它可以解码为 "AB"（1 2）或者 "L"（12）。

示例2：

输入：s = "226"

输出：3

解释：它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6)

示例3：

输入：s = "0"

输出：0

解释：没有字符映射到以 0 开头的数字。

含有 0 的有效映射是 'J' -> "10" 和 'T'-> "20" 。

由于没有字符，因此没有有效的方法对此进行解码，因为所有数字都需要映射。

本题第一感觉是个回溯问题，本题用回溯是可以的，问题仍然是容易超时，我们还是考虑一下DP怎么解决。
第一步：确定状态
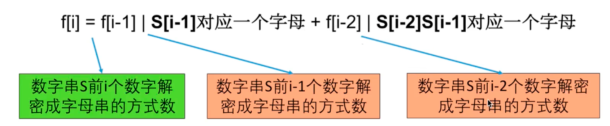
解密成为字母串，最后一定有最后一个字母，A、B..或Z，这个字母加密时变成1、2、....、26.
所以最后一个字母要么单独用了，要么和前面一个一起使用，假如说单独使用，例如下面这样子：

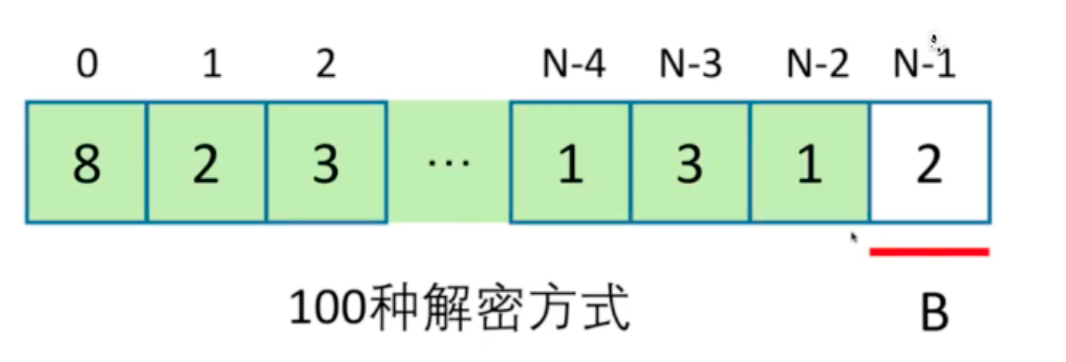
假如此时有100中解密方式。而如果将最后两个一起使用，也就是下面这样子：

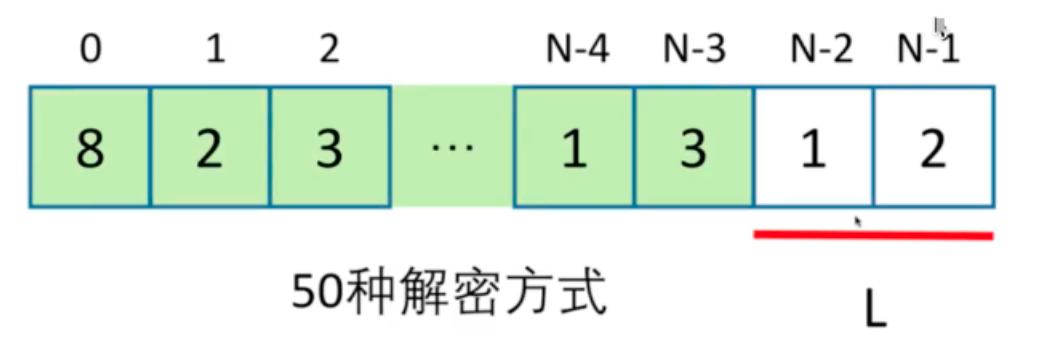假如此时有50种方法，那么总共方法就是100+50=150。
这样我们就得到了子问题：设数字串长度为N ，要求数字串前N个字符的解密方式数，此时需要知道数字串前面N-1和N-2字符的解密方式数。
所以本题的状态就是：设字符串S前i个数字解密成字母串有f[i]种方式。
第二步：确定状态转移方程
设数字S前i个数字解密成字母串有f[i]种方式，

第三步：确定初始条件和边界情况
初始条件f[0]=1，即空串有1种方式解密，解密成空串就行了。
边界情况：如果i=1，只看最后一个数字就行了。
第四步：按照顺序计算
f[0]，f[1]，f[2]，....,f[N]，答案就是f[N]

public static int numDecodings(String s) {
    int n = s.length();
    int[] f = new int[n + 1];
    f[0] = 1;
    for (int i = 1; i <= n; ++i) {
        if (s.charAt(i - 1) != '0') {
            f[i] += f[i - 1];
        }
        if (i > 1 && (check(s, i))) {
            f[i] += f[i - 2];
        }
    }
    return f[n];
}

public static boolean check(String s, int i) {
    if (s.charAt(i - 2) == '0') {
        return false;
    }
    if ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') > 26) {
        return false;
    }
    return true;
}

7 路径中存在障碍物?

我们在上面路径部分介绍了多种路径的问题，但是本专题还有个重要的拓展问题，就是假如网格中存在障碍物该怎么办。我们这里补充一下。
本题是在leetcode 62题要求的基础上，如果中间某个位置存在障碍物，那一共有多少种路径。假如在上面的网格中存在一个障碍物，你该怎么处理呢？

示例1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]

输出：2

解释：

3x3 网格的正中间有一个障碍物。

从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下

2. 向下 -> 向下 -> 向右 -> 向右

?

这个处理方法不算复杂，假如没有障碍物的格子标记为0，有障碍物的标记为1，那么执行的时候如果当前位置dp[i][j]==1时，直接跳过就行了。这么写：

public int uniquePathsWithObstacles(int[][] obstacleGrid) {
    int n = obstacleGrid.length, m = obstacleGrid[0].length;
    int[] dp = new int[m];
    dp[0] = obstacleGrid[0][0] == 0 ? 1 : 0;
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            if (obstacleGrid[i][j] == 1) {
                dp[j] = 0;
                continue;
            }
            if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
                dp[j] += dp[j - 1];
            }
        }
    }
    return dp[m - 1];
}

如果面试直接考63题，估计我们会崩溃，但是如果我们先将62题研究清楚了，63题是不是就很简单了？
面试算法最喜欢的是换换条件不断折腾，那这里我们能否再当一次面试官，假如有k个障碍物，k<min(m,n)，该怎处理呢？
其实，从代码的角度，我们什么都不用干，上面的代码就能执行，因为问题的关键在于传入进来的obstacleGrid数组包含多个元素1罢了，我们在双层循环里的这个判断足以处理。

if (obstacleGrid[i][j] == 1) {
    dp[j] = 0;
    continue;
}

这也是我们一直说的，一个方法可以解决大量的问题。一个问题改改条件就能造出大量的题目，我们后面还会继续折腾！

8 滚动数组技巧?

我们前面介绍了很多滚动数组的问题，本小节通过杨辉三角再来学习一种使用滚动数组的技巧。
杨辉三角是一种很出名的三角形，它的特点是每个元素都是其二维矩阵中左上方和右上方的元素之和，是一种对称结构，如下所示：

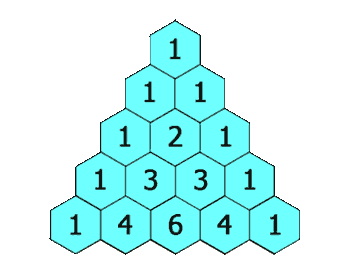
在LeetCode中对应118和119两道题，不同之处，一个是打印整个三角形，第二个是只需要打印出最后一行就行了。我们现在重点研究一下只打印最后一行的情况。
显然这个用二维数组比较可行，为了方便实现我们将其结构可以稍作改变，也就是：

观察上面的图，我们可以得到几个结论:
1.每一行最右侧和最左侧都是1。
2.前两行都是1，从第三行才开始有累加的问题。也就是这里的2，之后每行的元素仍然满足是其左上角+右上角元素之和。
3.每一行的元素数量都与其行数一样，所以可以为第N行建立一个大小为N的数组。
此时就可以写出如下的代码：

public class Yanghui {
    public static void main(String args[]) {
        //确定一个有10个数组（元素为数组）的二维数组
        int a[][] = new int[10][];
        //取出a[0],a[1]......a[9]十个数组
        for (int i = 0; i < a.length; i++) {
            //为10个数组确定空间（元素数目）
            a[i] = new int[i + 1];
            //将所有数组的第一个和最后一个元素元素赋值为1
            a[i][0] = 1;
            a[i][i] = 1;
        }

        //取出a[0],a[1]......a[9]十个数组
        for (int i = 0; i < a.length; i++) {

            //从第三个数组开始
            if (i > 1) {
                for (int j = 0; j < a.length; j++) {

                    //所有数组的第二个到倒数第二个元素，它们的值为前一个数组所对应的元素和前一个元素的和
                    //（a[2][1]=a[1][1]+a[1][0])
                    if (j > 0 && j < i) {
                        a[i][j] = a[i - 1][j] + a[i - 1][j - 1];
                    }
                }
            }
        }
        //通过下标访问数组的元素
        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < a[i].length; j++) {
                //这里使用print不进行自动换行，使用“\t”进行跳格（tab key即为空格键)
                System.out.print(a[i][j] + "\t");
            }
            //这里每进行一次for循环，都将结果进行换行
            System.out.println();
        }
    }
}

如果要得到最后一行，我们只要将二维数组的最后一行打印一下就可以了。
那如果要求只能使用O(n)空间实现，该怎么做呢？ 很显然我们可以使用上面提到的滚动数组来做，但是这里最大的问题是在二维数组的计算公式：
arr[i][j]=arr[i-1][j-1]+arr[i-1][j]
在计算dp[i]的时候，还需要上一轮的dp[i-1]，但是这个值已经被覆盖了，如下图所示标记的几个位置以及后序位置都是这样子。

例如图中的“3”号位置，我们需要使用上一轮的2和当前位置1相加，可惜如果只使用一个dp[i]数组的时候，这里的2已经被覆盖成3了。后面标记的6和4等等都是类似的情况，因此仅仅靠一个一维数组无法解决问题。
那怎么办呢？简单！使用两个数组，也是O(n)空间，使用两个数组来轮流交换，其中黑色表示上一轮的结构。红色表示当前轮要更新的结果。从下面图示可以清楚看到如何执行的。

对于网格上的动态规划，如果f[i][j]只依赖与本行的f[i][x]与前一行的f[i-1][y]那么就可以采用滚动数组来节省空间

public List<Integer> getRow(int rowIndex) {
    List<Integer> pre = new ArrayList<Integer>();
    for (int i = 0; i <= rowIndex; ++i) {
        List<Integer> cur = new ArrayList<Integer>();
        for (int j = 0; j <= i; ++j) {
            if (j == 0 || j == i) {
                cur.add(1);
            } else {
                cur.add(pre.get(j - 1) + pre.get(j));
            }
        }
        pre = cur;
    }
    return pre;
}

这种通过两个数组来实现空间优化的技巧在一些DP问题中经常使用，这里请同学们务必理解清楚。
如果说这里就是让你使用一个一维数组来完成，该怎么做呢？其实非常简单，观察上面的图我们会发现，当前行第 i 项的计算只与上一行第 i?1 项及第 i 项有关。因此我们可以倒着计算当前行，这样计算到第 i 项时，第i?1 项仍然是上一行的值。
验证一下执行是否有问题

public class Yanghui {
    public static  List<Integer> generate(int rowIndex) {
        List<Integer> row = new ArrayList<Integer>();
        row.add(1);
        for (int i = 1; i <= rowIndex; ++i) {
            row.add(0);
            for (int j = i; j > 0; --j) {
                row.set(j, row.get(j) + row.get(j - 1));
            }
        }
        return row;
    }

    public static void main(String[] args) {
        List<Integer> yanghui = generate(6);
        for (int i = 0; i < yanghui.size(); i++) {
            System.out.print(yanghui.get(i) + " ");
        }
    }
}

输出结果为：

1 6 15 20 15 6 1