详解C++位图/布隆过滤器+海量数据处理

目录

一、位图

1.1位图的概念

1.2位图的实现

1.3、位图应用面试题

二、布隆过滤器

2.1 布隆过滤器提出

2.2布隆过滤器概念

2.3 布隆过滤器模拟实现实现

2.3.1?布隆过滤器的插入

2.3.2?布隆过滤器的查找

2.3.3?布隆过滤器的删除

2.3.4 整体代码

三、海量数据处理

3.1 哈希切割

3.2 位图应用

3.2.1. 给定100亿个整数，设计算法找到只出现一次的整数？

3.2.2. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

3.2.3. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

3.3 布隆过滤器

3.3.1. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法

3.3.2如何扩展BloomFilter使得它支持删除元素的操作

---

一、位图

1.1位图的概念

所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

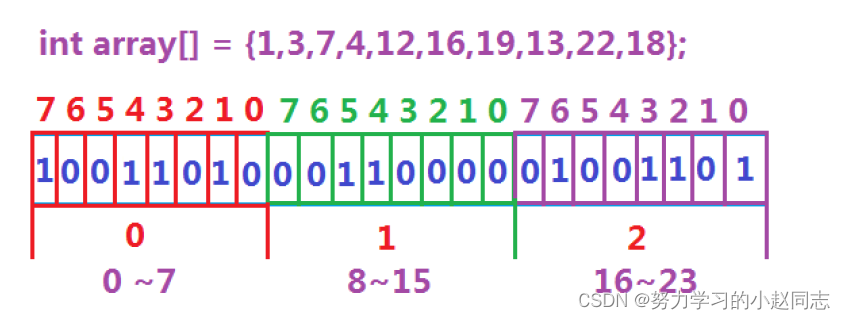
例：一个int类型的数据占用4个字节，即32个bit位，可以表示0-31的数是否存在。

1.2位图的实现

位图的实现主要是以下三个函数：set（）、reset（）、test（）。

1. 对于set，想要让某一比特位变为1其他位不变，则可以用1按位或对应的比特位，那就只需让1向高位移动j位，然后用位图中对应的字节进行按位或等即可。

2. 对于reset，想要让某一比特位变为0其他位不变，则可以用0按位与对应的比特位，那就只需让1向高位移动j位，然后按位取反，最后用位图中对应的字节进行按位与等即可。

3. 对于test，我们可以让对应比特位按位与1，其他比特位按位与0，这样其他比特位都是0，如果测试的比特位是1，则结果是非0，那就是true，如果测试的比特位是0，则结果是0，那就是false。

namespace zyl
{ 
// 非类型模板参数
template <size_t N>  //容量N个字节
class bitset
{
public:
	//构造函数
	bitset()
	{
		_bits.resize(N / 8 + 1, 0);//开辟最少一个字节的空间
	}
	//置位函数，将指定的位设置为1
	//因为我们用的char存储的数据，一个char为一个字节,
	void set(size_t x)
	{
		size_t i = x / 8;        //x/8 表明i是在vector中的哪一个字节当中
	                            
		size_t j = x % 8;        //j表明 在 vector 第i个字节中的第几位

		_bits[i] |= 1 << j;      //把vector 第i个字节中的第j位置1；
	}

    //复位函数，将指定位设置为0
	void reset(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		_bits[i] &= ~(1 << j);   //把vector 第i个字节中的第j位置0；
	}
	//访问函数，获取指定的位的值
	bool test(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;
		return _bits[i] & (1 << j);  //用& 只查看 不修改
	}
private:
	vector<char> _bits;
};
}

1.3、位图应用面试题

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】

1.我们常规的方法，直接遍历，时间复杂度O（N），但是40亿个数中寻找一个数，无异于大海捞针，直接遍历所消耗的时间还是很多，更别说我们用什么来存储这40亿个数?

2.利用二分查找法，二分查找法的时间复杂度为O(logN),时间复杂度来说很快，但是二分查找只适用于有序的数列，我们还得先进行排序，最快的快排也会消耗大量时间?

3.采用位图

首先，我们把数据存在对应的比特位，节省了大量的空间（42亿个数据换算比特位进行存储，也就是需要0.5GB，512MB内存申请是没有压力的。），然后一个比特位，只能显示0/1，正好我们用0/1代表数据是否存在。

二、布隆过滤器

2.1 布隆过滤器提出

我们在使用新闻客户端看新闻时，它会给我们不停地推荐新的内容，它每次推荐时要去重，去掉那些已经看过的内容。问题来了，新闻客户端推荐系统如何实现推送去重的？ 用服务器记录了用户看过的所有历史记录，当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选，过滤掉那些已经存在的记录。 如何快速查找呢？

1. 用哈希表存储用户记录，缺点：浪费空间
2. 用位图存储用户记录，缺点：不能处理哈希冲突
3. 将哈希与位图结合，即布隆过滤器

2.2布隆过滤器概念

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间。

2.3 布隆过滤器模拟实现实现

2.3.1?布隆过滤器的插入

一般的位图下，每一个数据只跟位图产生一个映射点，而且只能用于整型。但布隆过滤器是每一个数据可以有N个映射点，N个映射点对应于N个哈希函数，这个是我们自己定义的。用哈希函数将非整型转化成整型。映射多个位置，降低误判率

插入原理：添加一个元素时，用哈希函数计算出该元素在位数组中的多个位置，并将这些位置的值设为1

void set(const K& key)
		{
			//通过不同的哈希函数，让同一个数据可以计算出三个不同的位置
			size_t hash1 = HashFunc1()(key) % (N * X);
			size_t hash2 = HashFunc2()(key) % (N * X);
			size_t hash3 = HashFunc3()(key) % (N * X);

			//计算出位置后，使用位图的set方法将位图上对应的比特位进行0变1
			_bs.set(hash1);
			_bs.set(hash2);
			_bs.set(hash3);
		}

2.3.2?布隆过滤器的查找

分别计算每个哈希值对应的比特位置存储的是否为零，只要有一个为零，代表该元素一定不在哈希表中，否则可能在哈希表中。

bool test(cost K& key)
		{
			//先逐个位置判断，如果它是0，直接返回false
			size_t hash1 = HashFunc1()(key) % (N * X);
			if (!_bs.test(hash1))
			{
				return false;
			}
			size_t hash2 = HashFunc2()(key) % (N * X);
			if (!_bs.test(hash2))
			{
				return false;
			}
			size_t hash3 = HashFunc3()(key) % (N * X);
			if (!_bs.test(hash3))
			{
				return false;
			}
			//直到最后，说明该数据是存在的，返回true
			return true;
		}

2.3.3?布隆过滤器的删除

注意：布隆过滤器如果说某个元素不存在时，该元素一定不存在，如果该元素存在时，该元素可能存在，因为有些哈希函数存在一定的误判。

2.3.4 整体代码

namespace zyl
{
	struct BKDRHash
	{
		size_t operator()(const string& key)
		{
			size_t hash = 0;
			for (auto ch : key)
			{
				hash *= 131;
				hash += ch;
			}
			return hash;
		}
	};

	struct APHash
	{
		size_t operator()(const string& key)
		{
			unsigned int hash = 0;
			int i = 0;

			for (auto ch : key)
			{
				if ((i & 1) == 0)
				{
					hash ^= ((hash << 7) ^ (ch) ^ (hash >> 3));
				}
				else
				{
					hash ^= (~((hash << 11) ^ (ch) ^ (hash >> 5)));
				}

				++i;
			}

			return hash;
		}
	};

	struct DJBHash
	{
		size_t operator()(const string& key)
		{
			unsigned int hash = 5381;

			for (auto ch : key)
			{
				hash += (hash << 5) + ch;
			}

			return hash;
		}
	};

	template<size_t N,
		size_t X = 5,
		class K = string,
		class HashFunc1 = BKDRHash,
		class HashFunc2 = APHash,
		class HashFunc3 = DJBHash>
		class BloomFilter
	{
	public:
		void set(const K& key)
		{
			//通过不同的哈希函数，让同一个数据可以计算出三个不同的位置
			size_t hash1 = HashFunc1()(key) % (N * X);
			size_t hash2 = HashFunc2()(key) % (N * X);
			size_t hash3 = HashFunc3()(key) % (N * X);

			//计算出位置后，使用位图的set方法将位图上对应的比特位进行0变1
			_bs.set(hash1);
			_bs.set(hash2);
			_bs.set(hash3);
		}

		bool test(cost K& key)
		{
			//先逐个位置判断，如果它是0，直接返回false
			size_t hash1 = HashFunc1()(key) % (N * X);
			if (!_bs.test(hash1))
			{
				return false;
			}
			size_t hash2 = HashFunc2()(key) % (N * X);
			if (!_bs.test(hash2))
			{
				return false;
			}
			size_t hash3 = HashFunc3()(key) % (N * X);
			if (!_bs.test(hash3))
			{
				return false;
			}
			//直到最后，说明该数据是存在的，返回true
			return true;
		}

	private:
		std::bitset<N* X> _bs;
	};
}

三、海量数据处理

3.1 哈希切割

给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？

超过100G大小的文件，肯定不能直接放到内存中，而是通过将它切割，分成很多份。那么如何去切割呢？是平均分成100份，每一份1G？

如果平均切割，那么会导致的问题是：如果文件中有好几个相同的值，且分布不集中，此时平均切割就很可能使一个IP有很多份在很多小文件中。

因此不能平均切割，需要的是哈希切割。哈希切割就是通过取模，让取模结果相同的数据放到同一份小文件里面。

哈希切割后，通过map来对每一个小文件进行统计

如果小文件超过一个G呢？

不管什么情况上来先遍历子文件内容，将每个内容构造成键值对插入到map里面，如果map存不下，则在插入的过程中会出现内存不够的情况，insert会报错，那其实就是new结点失败，new失败是会抛异常的，我们只要捕获这个异常即可，此时说明这个子文件中大多是不同的IP，那么只需要递归哈希切分这个子文件即可。
如果map能够存的下，则正常统计出 出现次数最多的IP即可，无须进行其他任何操作。

3.2 位图应用

3.2.1. 给定100亿个整数，设计算法找到只出现一次的整数？

使用两个位图，分别记录每个整数出现的次数，如果出现0次，则两个位图都为0；

如果出现1次，则第一个位图为0，第二个位图为1。

俩次或两次以上 的为 第一个位图为1，第二个位图为1。

插入好后，去寻找 01 即可

3.2.2. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

思路1：先将一个文件的数据映射到位图中，然后用另外一个文件的数据去遍历，得到交集，需要注意去重。

思路2：分布将两文件映射到两个位图，然后通过两位图的与运算判断是否有交集。

3.2.3. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

这道问题跟第一个问题基本一样，就是让“01”（出现一次）和"10"（出现俩次）为需要找到的整数。如果出现"11"以上，那么就不行。

3.3 布隆过滤器

3.3.1. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法

精确算法：可以使用哈希切割的方法，将两个文件按照query的哈希值分割成若干个小文件，使得每个小文件的大小不超过内存限制。然后对每一对小文件，用散列表或者排序的方法找出其中的交集。最后将所有小文件的交集合并起来，就得到了两个大文件的交集。

近似算法：可以使用布隆过滤器的方法，先将一个文件中的所有query插入到一个布隆过滤器中，然后遍历另一个文件中的query，用布隆过滤器检查是否可能存在于第一个文件中。如果可能存在，则加入到候选集合中。最后再对候选集合进行一次精确匹配，就得到了两个大文件的近似交集。

3.3.2如何扩展BloomFilter使得它支持删除元素的操作

使用计数型布隆过滤器，即在每个位数组位置上不再存储一个比特位，而是存储一个计数器。当插入一个元素时，将其映射到的位数组位置上的计数器加一；当删除一个元素时，将其映射到的位数组位置上的计数器减一。这样就可以实现删除操作，但是会增加空间开销和计算复杂度 。

使用双重布隆过滤器，即维护两个布隆过滤器，一个用于存储插入的元素（A），一个用于存储删除的元素（B）。当插入一个元素时，将其加入到A中；当删除一个元素时，将其加入到B中。当查询一个元素时，先检查它是否在A中，如果不在，则认为不存在；如果在，则再检查它是否在B中，如果在，则认为已经删除；如果不在，则认为存在。这样也可以实现删除操作，但是会增加误判率和维护成本