数值最优化-KKT条件（一阶必要条件）证明总结

笔记：约束优化问题一阶最优性条件（KKT条件） - 知乎 (zhihu.com)

最优化理论与方法-第八讲-约束优化（一）：KKT条件_哔哩哔哩_bilibili

参考链接：如上

唯一参考书：数值最优化（numerical optimization）

• 等式约束的优化问题如下所示：

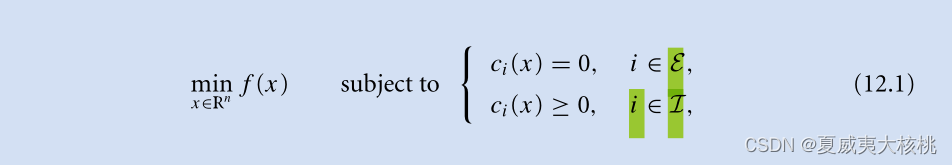
• ?引入active set(有效集)的基本概念：

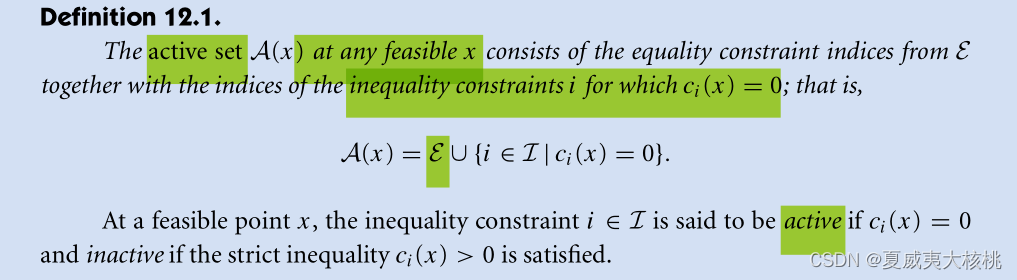
?简单的来说，对于一个可行点x，x的有效集就是这一点等式约束的方程的下标，和不等式约束中满足等号的方程的下标的集合。

• 引入tangent cone(切锥)：

?这里有两个地方容易忽视，第一：序列?是可行点序列，即这些所有的点都在约束范围内；第二：序列?是正的；切锥的定义中涉及到了cone的概念：

• 引入cone，可以看到cone的定义还是比较简单的。

• ?引入Linearized feasible directon(线性可行方向)：

?对切锥和线性可行方向更好的理解参考上面提到的知乎笔记。

• 然后是LICQ:

LICQ希望约束条件的导数是独立的，应该还是比较好满足的。

• 定理12.1就是要证明的KKT，这里先列出来：

• 进而定义Strict Complementarity(翻译成严格互补条件吗？)

这个定义就是指出了一个特殊情况，也就是说对于不等式的那些和，其中总有一个是0。

这一块后面没有用到。

• 插入一个证明特别复杂的引理，在后面会用到：

引理第二条给出：当LICQ满足时，切锥和线性可行方向相等。其实类似与LICQ这样的条件似乎还有几个。这条引理的证明看起来好复杂，目前还看不懂。

• 然后也是KKT证明需要的一个定理（加上两个引理，总共需要三个前置）。

定理 12.3指出：约束问题的解有如上性质。

• 然后是FARKAS引理：

• FARKAS定理写在一起就是：

这个引理在文中的证明方法是：首先证明两种情况不同时成立，其次证明一种情况不成立时，另一种成立。?

并在最后直接套用FARKAS的结果给出：

这个套用的过程的一个比较模糊的地方是等式12.50的求和部分应该分为两项：一项是有效集中的等式约束项，另一项是有效集中的不等式约束项，并在FARKAS引理中对分别对应和。?

• 最后使用这两个引理和定理12.3就可以得出定理12.1，过程如下：

????????等式12.52之前的一段给出了如何从假设是局部最优解，到证明出等式12.51的成立的全部脉络。但等式12.51并不直接等价于KKT条件12.34。因此，又通过补充条件12.52来证明，在这样定义的的情况下，KKT被完全满足。这里再次列出KKT条件。

????????首先是的定义式12.33（如下），加上得出的结果12.51，再加上补充条件12.52就可以直接得出12.34a，这里需要注意的是12.33式中求和下标是全部约束，而结论12.51给出的求和下标只有有效集，两者相差的部分就正是等式12.52所定义的在时的。因此等式12.34a被满足。

????????其次，由于是局部最优解，12.34b和12.34c自然被满足。

第三，结论12.51的范围，加上12.52中给出的范围，全部包括了的情况，因此，12.34d被满足。

? ? ? ? 最后，有效集中的都为0，有效集之外的不等式约束都为零，加在一起就有12.34e被满足。

????????至此，KKT条件被全部证明完毕。

????????到这里，数值最优化（numerical optimization）一书中的有关KKT条件的证明就算结束了。总的看来，证明的思路和表述十分清晰，但阅读后，对其中的切锥、线性可行方向、LICQ，引理12.2的理解都浮于表面而不深刻。希望以后有机会填坑。