代码随想录算法训练营第四十三天|1049. 最后一块石头的重量 II、 494. 目标和、474.一和零
发布时间:2024年01月24日
题目:1049. 最后一块石头的重量 II
文章链接:代码随想录
视频链接:LeetCode:1049.最后一块石头的重量||
题目链接:力扣题目链接
图释:
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
// 其实也是尽可能地将一堆石头分成两部分,它们相互抵消
vector<int> dp(1501,0); // 背包中最大石头的重量(30*100/2)
int sum = 0;
for(int i=0; i<stones.size(); i++){
sum += stones[i];
}
int target = sum/2; // 向下取整 [2,7,4,1,8,1] sum=23 target=11
// 即取背包dp[11] 中的最大重量
for(int i=0; i<stones.size(); i++){
for(int j=target; j>=stones[i]; j--){
// 从前向后遍历,物体重量大于背包重量,则退出
dp[j] = max(dp[j], dp[j-stones[i]]+stones[i]);
}
}
// sum-dp[target] 较大石头堆的重量 - dp[target]较小石头堆的重量
return sum-2*dp[target];
}
};
题目:494. 目标和
文章链接:代码随想录
视频链接:LeetCode:494.目标和
题目链接:力扣题目链接
图释:
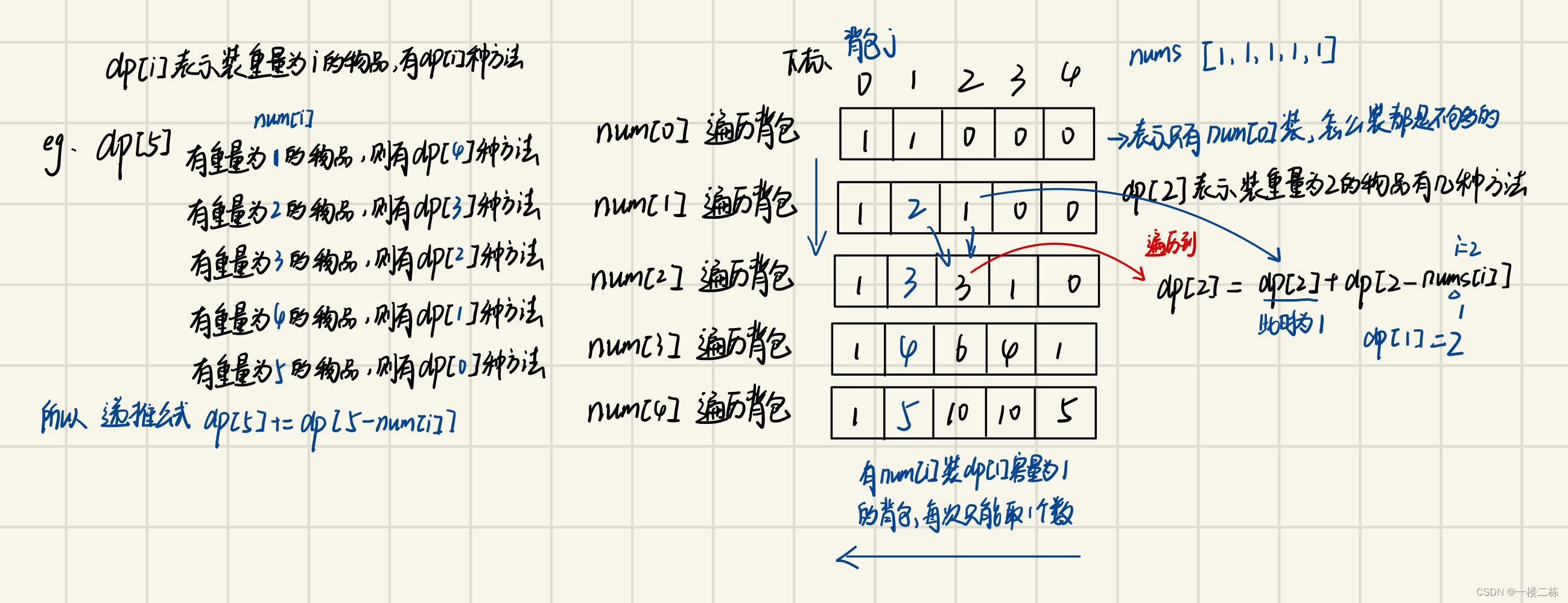
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum=0;
for(int i=0; i<nums.size(); i++){
sum += nums[i];
}
// 思路: 将数组分割成正负两个子集 left 和 right
// 即: left-right=target left+right=sum 合并得 left = (target+sum)/2
// 如果 不能整除2的话,则说明无法满足分割要求
if((target+sum)%2==1) return 0;
if(abs(target) > sum) return 0; // 目标的绝对值,大于非负整数数组总和,也不可能满足
int left = (target+sum)/2;
// dp[i]数组的含义, 满足背包容量为i,一共有dp[i]中方法
vector<int> dp(left+1, 0); // 因为是要求dp[left] 说最大为1001
dp[0]=1; //有待思考
for(int i=0; i<nums.size(); i++){
for(int j=left; j>=nums[i]; j--){
dp[j] += dp[j-nums[i]]; // 详见图解
}
}
return dp[left];
}
};题目:474.一和零
文章链接:代码随想录
视频链接:LeetCode:474.一和零
题目链接:力扣题目链接
图释:
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
// 本题的重点在于 物品的放入有两个维度约束,可以理解为 m是重量,n是体积
// dp[i][j] dp数组的含义为,装重量为i的物品,以及装j体积的物品,的最大个数(价值)
vector<vector<int>> dp(m+1, vector<int>(n+1, 0)); // 二维滚动数组,取max,为了不影响后面数值取值
for(string str : strs){ // 遍历物品
// 遍历每个字符串的01数量
int oneNum =0 , zeroNum =0;
for(char c:str){
if(c=='0')zeroNum++;
if(c=='1')oneNum++;
// 也可以这样 else oneNum++;
}
// 题目规定 m为0 n为1
for(int i=m; i>=zeroNum; i--){ // 背包重量从大到小装
for(int j=n; j>=oneNum; j--){
dp[i][j] = max(dp[i-zeroNum][j-oneNum]+1, dp[i][j]);
// 没装这个物品时的数量+1, 以及上一轮没用上这个物品时的最大数量
}
}
}
return dp[m][n];
}
};
文章来源:https://blog.csdn.net/m0_71413464/article/details/135813918
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- S7-1200PLC脉冲轴位置控制功能块(SCL代码)
- 国际化翻译navigator.language || navigator.userLanguage与语种对照表
- 实验笔记之——Gaussian Splatting
- MySQL使用问题记录
- Audio Precision SYS-2722音频分析仪
- eNSP学习——VLAN基础配置及Access接口
- JavaEE中的Controller的每一个Handler如何确定返回值与形参?
- centos搭建kubernetes集群步骤
- AAAI‘2024时间序列论文汇总!预测、分类、异常检测和因果发现的最新进展
- 投诉建议二维码制作系统“有意见,码上提”