Codeforces round 918(Div.4) (C--G)
C题

显而易见,C题问的就是所有方块大小之和是不是平方数。
所以只要定义一个函数来判断一个数是不是平方数就行,因为这道题时间限制够,我一开始用暴力枚举1--根号x的整数也AC了。不幸的是一早起来发现被HACK了,就换二分查来找到最靠近根号x的整数的数字了。
上代码:
#include<iostream>
using namespace std;
typedef long long ll;
bool square(ll x){
? ? ll l=1,r=x;
? ? while(l<r){
? ? ? ? ll mid=(l+r+1)/2;
? ? ? ? if(mid<=x/mid) l=mid;
? ? ? ? else r=mid-1;
? ? }
? ? if(l*l==x) return true;
? ? return false;
}
int main(){
? ? int t;
? ? cin>>t;
? ? while(t--){
? ? ? ? int n;
? ? ? ? cin>>n;
? ? ? ? ll sum=0;
? ? ? ? while(n--){
? ? ? ? ? ? ll a;
? ? ? ? ? ? cin>>a;
? ? ? ? ? ? sum+=a;
? ? ? ? }
? ? ? ? if(square(sum)) puts("YES");
? ? ? ? else puts("NO");
? ? }
? ? return 0;
}
D题

关于D题我们可以发现每个音节之间都要加上.? 。那么观察音节的构成我们会发现不论是什么音节,vowels前面一定有一个consonants。所以我们只需要循环判断vowels,如果两个vowels距离为2,那么两个vowels中间的consonants一定是后面的vowels的,所以要在第一个vowels后面加.(这个.与下一个vowels距离为2);如果两个vowels距离为3,那么两个vowels中间的第一个consonants一定是前者的,第二个一定是后者的,所以要在第一个consonants后面加.(这个.与下一个vowels距离也为2);所以只需要判断当前位置的后面第二个位置是不是vowels,如果是的话输出.即可
上代码:
#include<iostream>
using namespace std;
int main() {
? ? int t;
? ? cin>>t;
? ? while(t--){
? ? ? ? int n;
? ? ? ? cin>>n;
? ? ? ? string s;
? ? ? ? cin>> s;
? ? ? ? for(int i=0;i<n-2;i++){
? ? ? ? ? ? cout<<s[i];
? ? ? ? ? ? if(s[i+2]=='a'||s[i+2]=='e') cout<<".";
? ? ? ? }
? ? ? ? cout<<s[n-2]<<s[n-1]<<endl;
? ? }
? ? return 0;
}
E题?

E题是判断给定序列是否存在一个子序列使得其中的奇数项和与偶数项和相等。
这道题我们可以将序列的奇数项赋值为负数。那么只需要求一个子序列里的所有项的和为0即可,那么我们需要求出给定序列的前缀和s1[n],那么只要满足s1[r]-s1[l-1]==0即有两个相同的s就可以符合题目条件。这里我们可以开一个set来储存s1[i] 的值,一边赋s1[i]的新值一边存储。当我们赋的新值在set中时,就可以判断满足题目条件。
上代码:
#include<iostream>
#include<set>
using namespace std;
const int N=2e5+10;
typedef long long ll;
set<ll> s;
ll a[N];
ll s1[N];
int main(){
? ? int t;
? ? cin>>t;
? ? while(t--){
? ? ? ? s.clear();
? ? ? ? int n;
? ? ? ? cin>>n;
? ? ? ? for(int i=1;i<=n;i++){
? ? ? ? ? ? cin>>a[i];
? ? ? ? ? ? if(i%2==1) a[i]*=-1;
? ? ? ? }
? ? ? ? bool flag=false;
? ? ? ? s.insert(0);
? ? ? ? for(int i=1;i<=n;i++){
? ? ? ? ? ? s1[i]=s1[i-1]+a[i];
? ? ? ? ? ? if(s.count(s1[i])){
? ? ? ? ? ? ? ? flag=true;
? ? ? ? ? ? ? ? break;
? ? ? ? ? ? }
? ? ? ? ? ? s.insert(s1[i]);
? ? ? ? }
? ? ? ? if(flag) puts("YES");
? ? ? ? else puts("NO");
? ? }
}
F题
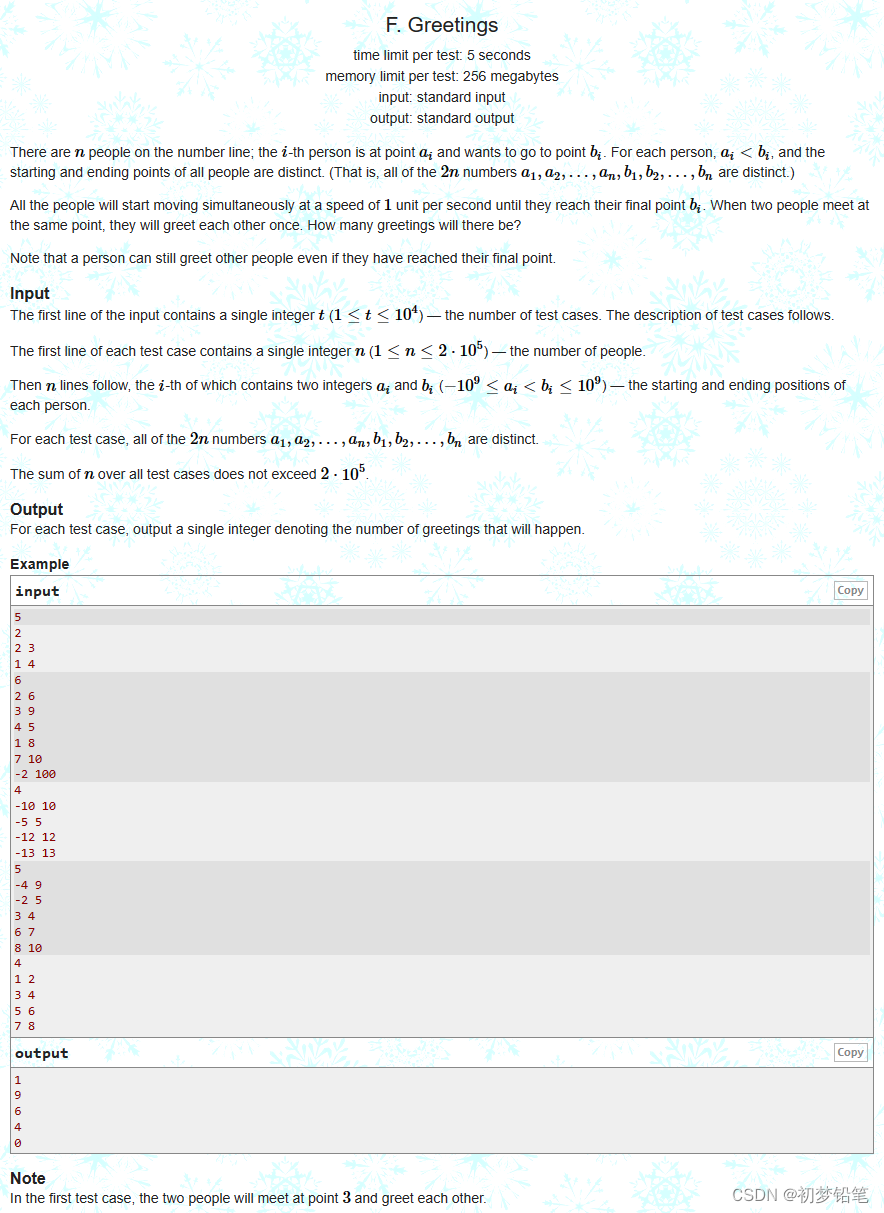
F题讲述了这样一个数学问题:每个测试点都有n个选手,每个选手都从各自的起点走到终点,而且他们速度一样,他们如果相遇了就会互相打招呼,题目就是让我们解出打招呼的次数。
首先,我们要思考怎么样的两位选手会相遇打招呼,我们速度可以通过看给定的案例发现,如果一名选手a的起点在选手b前面,而且a的终点在选手b的右边,那么a和b一定会打一次招呼,那么我们只需要按所有选手的起点从小到大排序,然后计算每一个选手其后续节点的终点在该选手的终点的右边的数量(这样是不会重复和遗漏的),那么我们可以将数据存到pair中,然后按照起点排序接着按照终点算逆序对即可。
上代码:
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=2e5+10;
int temp[N];
typedef pair<int,int> pii;
int n;
ll merge_sort(int q[],int l,int r){? ?//太菜了只会用归并排序算逆序对
? ? if(l>=r) return 0;
? ? int mid=l+r>>1;
? ? ll res=merge_sort(q,l,mid)+merge_sort(q,mid+1,r);
? ? int k=0,i=l,j=mid+1;
? ? while(i<=mid&&j<=r){
? ? ? ? if(q[i]<=q[j]) temp[k++]=q[i++];
? ? ? ? else{
? ? ? ? ? ? temp[k++]=q[j++];
? ? ? ? ? ? res+=mid-i+1;
? ? ? ? }
? ? }
? ? while(i<=mid) temp[k++]=q[i++];
? ? while(j<=r) temp[k++]=q[j++];
? ? for(int i=l,j=0;i<=r;i++,j++) q[i]=temp[j];
? ? return res;
}
void solve(){
? ? cin>>n;
? ? pii a[n];
? ? for(int i=0;i<n;i++){
? ? ? ? cin>>a[i].first>>a[i].second;
? ? }
? ? sort(a,a+n);? ? //按照起点排序
? ? int b[n];? ? ?//将终点全部存到b数组里面然后求b数组的逆序对
? ? for(int i=0;i<n;i++){
? ? ? ? b[i]=a[i].second;
? ? }
? ? cout<<merge_sort(b,0,n-1)<<endl;
}
int main(){
? ? int t;
? ? cin>>t;
? ? while(t--){
? ? ? ? solve();
? ? }
? ? return 0;
}
G题

G题对于我这个蒟蒻来说真的挺困难的,但是在借鉴了各方大佬的思路和代码后,我终于解决了。
首先这道题问的是从城市1到城市n的最小时间花费,所以可以想到用最短路来写,但是题目里出现了不同的slowness(后面我们称它为s)值,s值越小,就代表速度越快,所以我们可以有两个决策,要么选择用当前最快的bike走最短路,要么去找更快的bike再去走路。为了比较两者具体哪个决策更优我们可以将所有点以s来排序,记ans(i)为从i点开始到终点的最少消耗,那么s最小的点x他的ans(x)必然是从他本身直接走最短路到终点的消耗,那么s第二小的点y他的ans(y)是要么从他本身直接走最短路到终点的消耗,要么是先走到x点的消耗再加上ans(x)....以此类推可以算出所有点到终点的最短消耗,即可解决问题。(这里用spfa可以过时间限制)
上代码:
#include<algorithm>
#include<vector>
#include<queue>
#include<iostream>
using namespace std;
const int N=2e6+10;
typedef long long ll;
typedef pair<int,int> pii;
vector<pii>e[N];
struct city{
? ? int id,s;
? ? bool operator<(const city &W)const{? ? ?//s小的排序在前面
? ? ? ? return s<W.s;
? ? }
}a[N];
ll ans[N];
int n,m;
void spfa(int x,ll s){? ? //用队列来实现spfa算法
? ? vector<ll> dis(n+1,1e9);
? ? queue<int>q;
? ? q.push(x);
? ? dis[x]=0;
? ? while(!q.empty()){
? ? ? ? int h=q.front();
? ? ? ? q.pop();
? ? ? ? for (int i = 0; i < e[h].size(); i++) {
? ? ? ? ? ? int ne = e[h][i].first;
? ? ? ? ? ? int now_dis = e[h][i].second;
? ? ? ? ? ? if (now_dis + dis[h] < dis[ne]) {? ?//dis的一个松弛过程
? ? ? ? ? ? ? ? dis[ne] = dis[h] + now_dis;
? ? ? ? ? ? ? ? q.push(ne);
? ? ? ? ? ? }
? ? ? ? }
? ? }
? ? ans[x]=dis[n]*s;
? ? for(int i=1;i<n;i++){
? ? ? ? if(i!=x&&ans[i]!=-1) ans[x]=min(ans[x],ans[i]+dis[i]*s);? //比较从x点直接走最短路的消耗和先走到i点再走路的消耗哪个小,并选择更小值
? ? }
}
void solve(){
? ? cin>>n>>m;
? ? for(int i=1;i<=n;i++){? //记得每次的初始化
? ? ? ? e[i].clear();
? ? ? ? ans[i]=-1;
? ? }
? ? for(int i=1;i<=m;i++){
? ? ? ? int a,b,w;
? ? ? ? cin>>a>>b>>w;
? ? ? ? e[a].push_back({b,w});
? ? ? ? e[b].push_back({a,w});
? ? }
? ? for(int i=1;i<=n;i++){
? ? ? ? cin>>a[i].s;
? ? ? ? a[i].id=i;
? ? }
? ? sort(a+1,a+1+n);? ? //按照s的大小来排序
? ? for(int i=1;i<=n;i++){
? ? ? ? spfa(a[i].id,a[i].s);
? ? }
? ? cout<<ans[1]<<endl;
}
int main(){
? ? int t;
? ? cin>>t;
? ? while(t--) solve();
? ? return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【PHP入门】1.1-PHP初步语法
- Redis之集群脑裂
- 生成模型 | GAN系列生成系列论文及代码调研总结
- QtAV:基于Qt和FFmpeg的跨平台高性能音视频播放框架
- 使用割平面方法时,若其中一个约束中含有三个或三个以上变量该怎么操作
- 自学网络安全|一个寒假,能成为黑客吗?
- element ui Checkbox 多选框组件 lable不支持Object类型的值的问题
- 优化改进YOLOv5算法之Dilation-wise Residual(DWR)可扩张残差注意力模块,增强多尺度感受野特征,助力小目标检测
- 20.云原生之GitLab CICD实战
- RK3568驱动指南|第十篇 热插拔-第117章uevent_helper实验