数据结构期末模拟试卷
一、判断题
1.关键路径是AOE网中从源点到汇点的最短路径。(F)
在AOE网中,从源点到汇点最长的路径称为关键路径,在关键路径上的活动称为关键活动
2.?二叉排序树的查找效率和二叉排序树的髙度有关。(T)
最好情况:n 个结点的二叉树最小高度为? l o g 2 n ? + 1
最坏情况:每个结点只有一个分支,树高h =结点数n 平均查找,长度ASL=O ( n )?
3.?有n个数存放在一维数组A[1..n]中,在进行顺序查找时,这n个数的排列有序或无序其平均查找长度不同。(F)
列表长度为n,假设查找每个数据元素的概率相同,都为p=1/n,则ASL=1/2(n+1),所以在进行顺序查找,其平均查找长度相同。
4.通过对堆栈S操作:Push(S,1), Push(S,2), Pop(S), Push(S,3), Pop(S), Pop(S)。输出的序列为:123。(F)
栈:1 2
pop:2
栈:1 3
pop:3
pop:1
所以输出的序列为2 3 1
5.在任何情况下,时间复杂度为O(n2) 的算法比时间复杂度为O(n*logn)的算法所花费的时间都长。?(F)
数据规模小的时候,两者花费的时间差不多
6.?度为二的树就是二叉树。(F)
二叉树的定义:
1.每个结点的度都不大于2(即<=2)
2.每个结点的孩子结点次序不能任意颠倒。(有序树)
7.?装填因子是散列表的一个重要参数,它反映散列表的装满程度。(T)
装填因子a=哈希表中元素的个数/哈希表的长度
装填因子可以描述哈希表的装满程度。显然,装填因子越小,发生冲突的可能性越小
二、单选题?
1.具有35个顶点,997条边的有向图,所有顶点度的和为( A).
A.1994
B.70
C.595
D.997
997*2=1994
顶点度之和=边的条数*2;
2.?在一个单链表中,已知b结点,若在b后插入a结点,则须执行( B).
A.b->next=a; a->next=b;
B.a->next=b->next; b->next=a;
C.a->next=b; b->next=a->next
D.b->next=a->next; a->next=b;
?先拉右手,再拉左手,
b ?b->next
b a b->next
右手:a->next=b->next;
左手:b->next=a;
3.在下列关于二叉树遍历的说法中,正确的是( )。
A.若有一个结点是二叉树中某个子树的前序遍历结果序列的最后一个结点,则它一定是该子树的中序遍历结果序列的最后一个结点
B.若有一个叶子结点是二叉树中某个子树的中序遍历结果序列的最后一个结点,则它一定是该子树的前序遍历结果序列的最后一个结点
C.若有一个结点是二叉树中某个子树的中序遍历结果序列的最后一个结点,则它一定是该子树的前序遍历结果序列的最后一个结点
D.若有一个叶子结点是二叉树中某个子树的前序遍历结果序列的最后一个结点,则它一定是该子树的中序遍历结果序列的最后一个结点

4.有29个叶子的哈夫曼树的结点总数为 ( C).
A.58
B.840
C.57
D.59
假设度为0 的结点为x,则度为2的节点为x-1
所以结点总数为:x+x-1=29+28=57
叶子结点是度为0 的结点
5.具有48个顶点的无向图至少有多少条边才能形成连通图 (C ).
A.1128
B.49
C.47
D.48

当有n个顶点的时候,最少需要n-1条边可以组成连通图
6.?一棵二叉树,度为2结点数为70,度为1结点数为176,则叶子结点数为(B ).
A.177
B.71
C.175
D.69
度为2的结点数为70,度为0的结点数为71(叶子结点数)
7.?假设以行序为主序存储二维数组A=array[1..80,1..100],设每个数据元素占2个存储单元,基地址LOC[1,1]为7500,则LOC[75,8]的存储位置为( B).
A.22316
B.22314
C.22514
D.22516
A=arry[1..m,1...n],设每个数据元素占b个存储字节
Loc(i,j)=Loc(1,1)+[n×(i-1)+j-1]×b,
loc(75,8)=loc(1,1)+[100*74+7]*2=7500+7407*2=22314
8.?已知序列11,30,37,44,60,71,80,97,102,108,119,则用折半查找法查找44需要进行(A )次比较.
A.3
B.2
C.4
D.1
[log2(11)]=3;
三、填空题?
1.已知哈希表长度为 8,哈希函数为?H(k)=kmod7,采用线性探测法处理冲突。
将下列关键字依次插入到哈希表中,
34, 37, 20, 16, 13
请写出存入数据后的哈希表。
1.34/7=4....6(6,1)
2.37/7=5....2(2,1)
3.20/7=2....6(7,2)
4.16/7=2....2(3,2)
5.13/7=1....6(0,3)
(1+1+2+2+3)/5=9/5=1.8
| 0 | 13 |
| 1 | - |
| 2 | 37 |
| 3 | 16 |
| 4 | - |
| 5 | - |
| 6 | 34 |
| 7 | 20 |
注:空白处填“-”。
若各关键字的检索概率相等,则平均查找长度为 1.8
2.如果二叉树的后序遍历结果是FDEBGCA,中序遍历结果是FDBEACG,那么该二叉树的前序遍历结果是:ABDFECG
中序遍历:FDBEACG? (左、根、右)
后序遍历:FDEBGCA (左、右、根)
1.先根据后序遍历,选出整个树的根节点为A;
2.再在中序遍历中,找到A所在的位置,A的左边为整个树的左子树,A的右边为整个树的右子树。
3.先看左子树,(FDBE),在后序遍历中找到这四个节点,可以发现(FDEB)中B为左子树的根节点,B的左孩子为D,B的右孩子为E,后序遍历(FD)中,D为根,D的左孩子为F
4.看右子树,后序遍历(GC)中,C为根,再看中序遍历(CG)中,C的右孩子为G.
?
由此图,可以看出前序遍历为:ABDFECG?
3.链接存储的特点是利用指针来表示数据元素之间的逻辑关系。
4.算法的量度
(1) 算法所需执行时间的量度称为 时间复杂度
(2) 算法所需存储空间的量度称为 空间复杂度
5.如图所示的AOE-网,求这个工程最早可能在什么时间结束?(18)
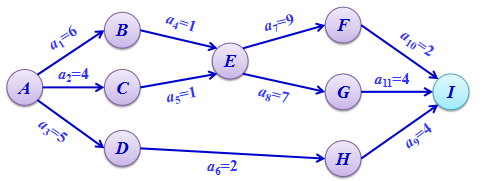
A到I点的最远距离的长度?:6+1+9+2=18;
6.?对如下图所示的AOE网络(A为源点,J为汇点),计算各事件(顶点)的最早发生时间和最晚发生时间。
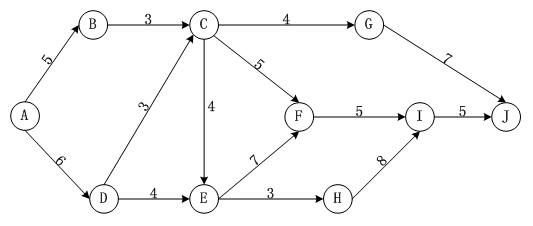
| 顶点 | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| Ve(i) | 0 | 5 | 9 | 6 | 13 | 20 | 13 | 16 | 25 | 30 |
| Vl(i) | 0 | 6 | 9 | 6 | 13 | 20 | 23 | 17 | 25 | 30 |
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!