【雷达原理】雷达测速原理及实现方法

发布时间：2023年12月23日

一、雷达测速原理

1.1 多普勒频率

?当目标和雷达之间存在相对运动时，若雷达发射信号的工作频率为 $eq?f_%7B0%7D$ ，则接收信号的频率为 $eq?f_%7B0%7D+f_%7Bd%7D$ ，其中 $eq?f_%7Bd%7D$ 为多普勒频率。将这种由于目标相对于辐射源运动而导致回波信号的频率发生变化的现象称为多普勒效应。

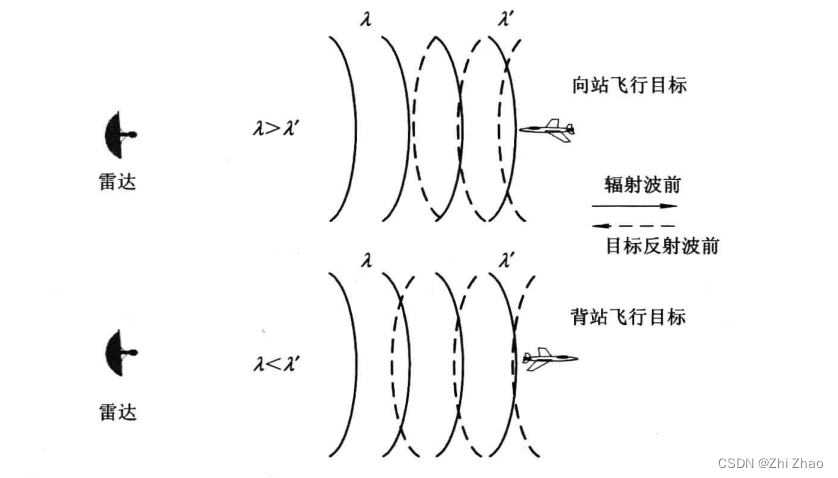
如图1-1所示，照射到目标上的波形具有间隔为 $eq?%5Clambda$ (波长)的等相位波前，靠近雷达的目标导致回波信号的等相位波前相互靠近(回波信号的波长 $eq?%7B%5Clambda%7D%27$ 较短)，即 $eq?%5Clambda%20%3E%7B%5Clambda%20%7D%27$ ；反之，远离雷达的目标导致回波信号的等相位波前相互扩展(回波信号的波长 $eq?%7B%5Clambda%7D%27$ 较长)，即 $eq?%5Clambda%20%3C%7B%5Clambda%20%7D%27$ 。

所以有以下结论：当目标靠近雷达运动时，多普勒频率为正；当目标远离雷达运动时，多普勒频率为负。

下面将给出多普勒频率的计算公式，其证明过程可以参考书本上的推导。

设目标的径向速度为 $eq?v$ ，则目标回波信号的多普勒频率为：

$eq?f_%7Bd%7D%3D%5Cfrac%7B2v%7D%7B%5Clambda%20%7D$ ，目标靠近雷达

$eq?f_%7Bd%7D%3D%5Cfrac%7B-2v%7D%7B%5Clambda%20%7D$ ，目标远离雷达

1.2 与速度有关的概念

通过发射两个时间间隔为Tc的线性调频信号，则接收到的每个脉冲对应的距离维FFT将在同一个位置具有峰值，但是峰值对应的相位不同。这两个峰值具有相位差，其与目标相对雷达运动产生的多普勒频率相关。

所以，当目标以速度v运动时，对应的相位差为：

$eq?%5Comega%20%3D2%5Cpi%20f_%7Bd%7DT_%7Bc%7D%3D%5Cfrac%7B4%5Cpi%20vT_%7Bc%7D%7D%7B%5Clambda%7D$ ? ? ? ? ? ? ? ? ?(1.2-1)

利用式(1.2-1)可计算出运动目标的速度。

(1) 最大测量速度

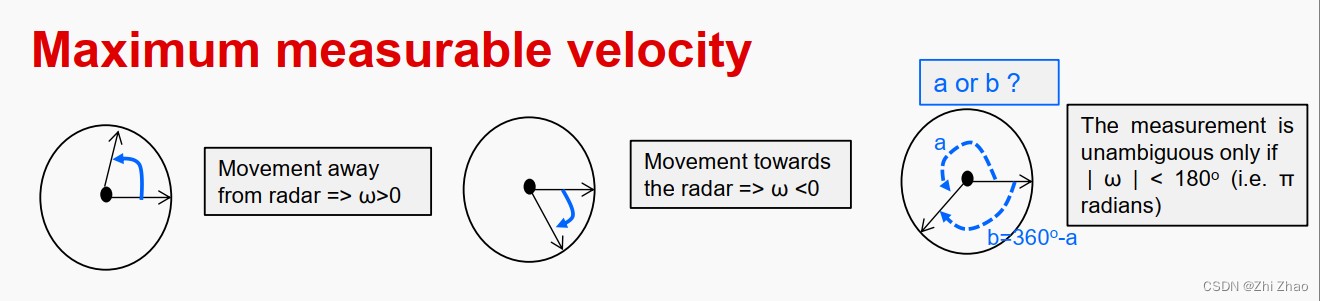
只有相位差满足 $eq?%5Cleft%20%7C%20%5Comega%20%5Cright%20%7C%20%3C%5Cpi$ ，才可以清楚的测量目标的速度，否则会出现速度模糊。

$\left | \omega \right | <\pi\Rightarrow \frac{4\pi vT_{c}}{\lambda}<\pi \Rightarrow v<\frac{\lambda}{4T_{c}}$ ? ? ? ? ? ? ?(1.2-2)

由此可得，当雷达以脉冲重复周期Tc发射信号时，可测量目标的最大不模糊速度为：

$v_{max} = \frac{\lambda}{4T_{c}}$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(1.2-3)

(2) 速度分辨率

当雷达前方有两个位置相近而速度不同(v1,v2)的目标时，我们可以发射一系列等间隔的线性调频信号对其进行测量，则距离维FFT的峰值位置相同，但这些峰值对应的离散序列有两个旋转向量(w1,w2)，即回波信号的角频率。

帧：将N个等间隔周期的线性调频信号称为一帧；

多普勒维FFT：一帧脉冲间进行FFT，也称为速度维FFT；

雷达的速度分辨能力取决于多普勒维FFT的频率分辨率，两个速度差为△v的目标回波信号的角频率间隔为△w：

$\Delta \omega =\frac{4\pi \Delta vT_{c}}{\lambda }$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (1.2-4)

由离散傅里叶变换的特性可知，要分辨这两个角频率，需要满足：

$\Delta \omega >\frac{2\pi }{N}$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (1.2-5)

联合式(1.2-4)和式(1.2-5)可得：

$\Delta v > \frac{\lambda }{2NT_{c}}$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (1.2-6)

因而，速度分辨率为：

$v_{res} = \frac{\lambda }{2NT_{c}}$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ?(1.2-7)

(3) 速度点精度

设一帧的脉冲数为N，对其进行多普勒维FFT的点数为 $N_{fft}$ ，则完成FFT的运算后，速度维上的每一个点代表的速度为：

$V_{point}=\frac{v_{max} }{\frac{N_{fft}}{2}}= \frac{\lambda}{2N_{fft}T_{c}}$ ? ? ? ? ? ? ? ? ? ? ? ? （1.2-8）

若 $N_{fft}=N$ ，则有：

$V_{point}= \frac{\lambda}{2NT_{c}}$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??? ?(1.2-9)

二、动目标检测(MTD)技术

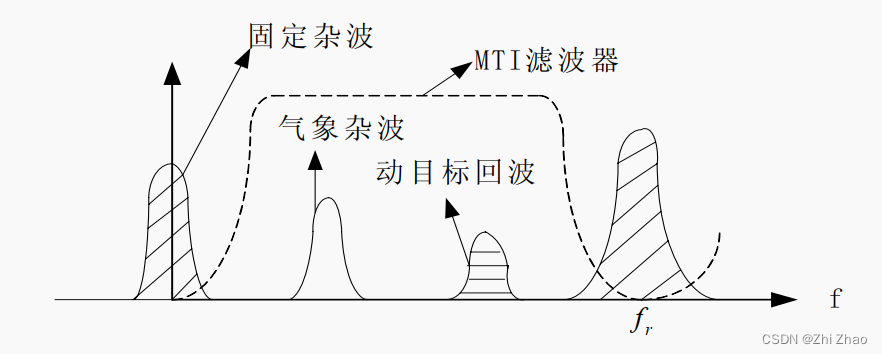
MTI滤波器虽然可以抑制杂波信号，但无法区分具有不同速度的运动目标回波信号，导致雷达无法实现对具有相同距离不同速度的运动目标的检测。动目标检测(Moving Target Detection，MTD)技术采用一组相邻且部分重叠的滤波器组，覆盖目标的整个多普勒频率范围，从每个滤波器的输出，获取对应目标的多普勒频率，从而得到运动目标的速度。

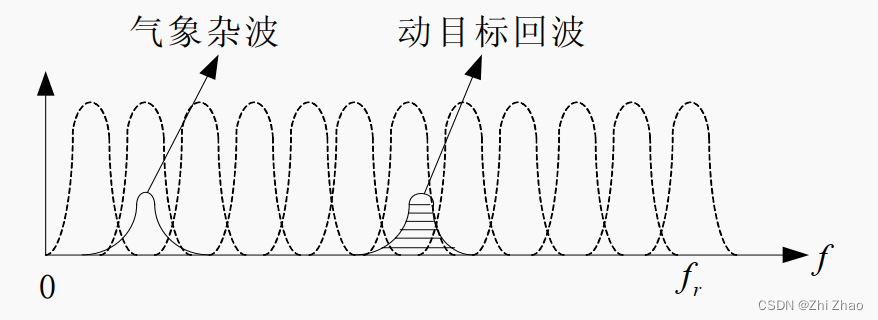
在工程应用中，通常采用(MTI+MTD)的方式，先利用MTI滤波器将雷达探测到的杂波及低速运动目标滤除，再采用MTD滤波器将不同速度的运动目标进行区分。

2.1 MTD算法原理

MTD算法的实现方式有两类：时域上采用FIR滤波器，频域上采用离散傅里叶变换(DFT)。对脉冲压缩后的数据，在同一距离单元的多个脉冲采用FFT进行处理，可得到不同速度的运动目标。

具有N个输出的横向滤波器，经过各重复周期的不同加权求和后，可以作为N个相邻的窄带滤波器组。其原理性结构如图2-3所示。

每个滤波器的权值可表示为：

$N%7D$

其中，i为滤波器的下标，k为同一距离单元的脉冲序列的下标，i=0,1,2,N-1，k=0,1,2,N-1。

可以得到MTD滤波器组的输入 $eq?x%28i%29$ 与输出 $eq?y%28k%29$ 的对应关系为：

$N%7D%2Ck%3D0%2C1%2C2%2C...%2CN-1$

上式与DFT的计算公式是等效的，所以可以用DFT实现MTD滤波器组。当N的取值为2的正整数次幂时，则可以采用DFT的快速算法——快速傅里叶变换(FFT)进行计算。

2.2 MTD算法仿真

设定3个目标，其距离分别为300米，600米，900米，速度分别为0m/s，10m/s，-15m/s，RSC分别为0.1㎡，1㎡，5㎡，利用上述目标参数产生模拟回波信号，对该信号进行二维FFT，即先在距离维上进行FFT，再对其多普勒维进行FFT，计算结果如图目标幅度值与目标的RCS及距离有关。

三、MATLAB仿真代码

clc;
clear;
close all;

%% LFM信号参数
B = 25e6;               % 带宽
T_chirp = 100e-6;       % 脉冲宽度
PRF = 1/T_chirp;        % 脉冲重复频率
u = B/T_chirp;          % 调频斜率
fs = 2*B;               % 采样率
NumADC = T_chirp*fs;       % 单个脉冲的采样点数
NumChirp = 128;             % 脉冲数
c = physconst('LightSpeed');        % 光速
f0 = 77e9;                          % 载频
Lambda = c/f0;                      % 波长

R_max = fs*c/(2*u);                 % 最大测量距离
V_max = Lambda*PRF/4;               % 最大测量速度

%% 目标参数
tarNum = 3;
tar_R0 = [300,600,900];           % 目标距离
tar_V0 = [0,10,-15];           % 目标速度
Rcs = [0.1,1,5];

%% 模拟信号
Tt = linspace(0,T_chirp*NumChirp,NumADC*NumChirp);
Phase_t = @(f0,u,t) 2*pi*(f0*t+1/2*u*t.^2);        % LFM信号的相位表达式

Signal_Tx = exp(1j*Phase_t(f0,u,Tt));           % 发射信号
Signal_Rx = 0;
for kk = 1:tarNum
    tar_R = tar_R0(kk)+tar_V0(kk)*Tt;
    tao = 2*tar_R/c;                % 目标回波的时延
    Ar = Rcs(kk)./(tar_R.^4);       % 目标回波幅度
    Signal_Rx = Signal_Rx + Ar.*exp(-1j*Phase_t(f0,u,(Tt-tao)));        % 接收信号
end

% 混频
Signal_Mix = Signal_Tx.*Signal_Rx;

rawData = reshape(Signal_Mix,NumADC,NumChirp);
clear Signal_Tx;
clear Signal_Rx;
clear Signal_Mix;

%% 距离维FFT
Nfft1 = 4096;            % FFT点数
R_point = (fs/Nfft1)*c/(2*u);    % 距离点精度
delta_R = c/(2*B);              % 距离分辨率

win1 = hamming(NumADC);       % 加窗
fft_Data = zeros(Nfft1,NumChirp);
for ii = 1:NumChirp
    fft_Data(:,ii) = fft(rawData(:,ii).*win1,Nfft1);
end

x1 = (1:NumChirp)';
y1 = R_point*(0:Nfft1-1)';
figure(101);
mesh(x1,y1,mag2db(abs(fft_Data)));xlabel('脉冲数');ylabel('距离维');title('1维FFT');
ylim([0 2000]);


%% 速度维FFT
win2 = hamming(NumChirp);       % 加窗
Nfft2 = NumChirp;
fft2D_Data = zeros(Nfft1,Nfft2);
for ii = 1:Nfft1
    fft2D_Data(ii,:) = fft(fft_Data(ii,:).*win2',Nfft2);
end

V_point = Lambda*PRF/(2*Nfft2);
figure(103);
mesh(x1,y1,mag2db(abs(fft2D_Data)));xlabel('速度维');ylabel('距离维');title('MTD');
ylim([0 2000]);

参考文献

[1]陈伯孝, 等. 现代雷达系统分析与设计[M]. 西安：西安电子科技大学出版社, 2012.9.

[2]?Introduction to mmwave Sensing：FMCW Radars.

文章来源:https://blog.csdn.net/weixin_45317919/article/details/133966723
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！