传感器原理与应用复习—测量概述与测量误差

测量概论

通常的测量结果包括比值和测量单位
测量结果的完整描述应包括估计值，测量单位及测量的不确定度（误差）

测量分类：

1. 根据测得的值是否直接使用

   • 直接测量：不需要经过任何运算，直接得到被测量的数值
   • 间接测量：将直接测得的值带入函数关系式，经过计算得到所需要的结果
   • 组合测量：若被测量必须经过求解联立方程组求得，称为组合测量

2. 根据测量方法分为：偏差式测量，零位法测量与微差法测量

   • 偏差式： 用仪表指针的位移决定被测量的量值
   • 零位式：用指零仪表的零位反应测量系统的平衡状态，用已知的标准量决定被测量的量值
   • 微差式：将被测量量与已知标准量相比较，取得差值后，在用偏差法测得此差值

检测系统：

1. 开环系统
   
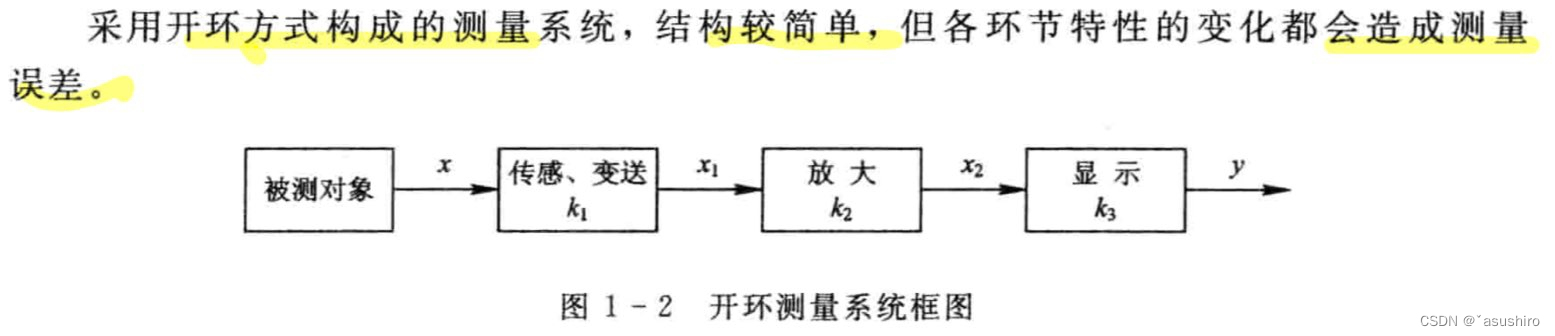
   开环系统输入输出关系$$y=k_1{k}_2{k}_{3}x$$

2. 闭环系统
   
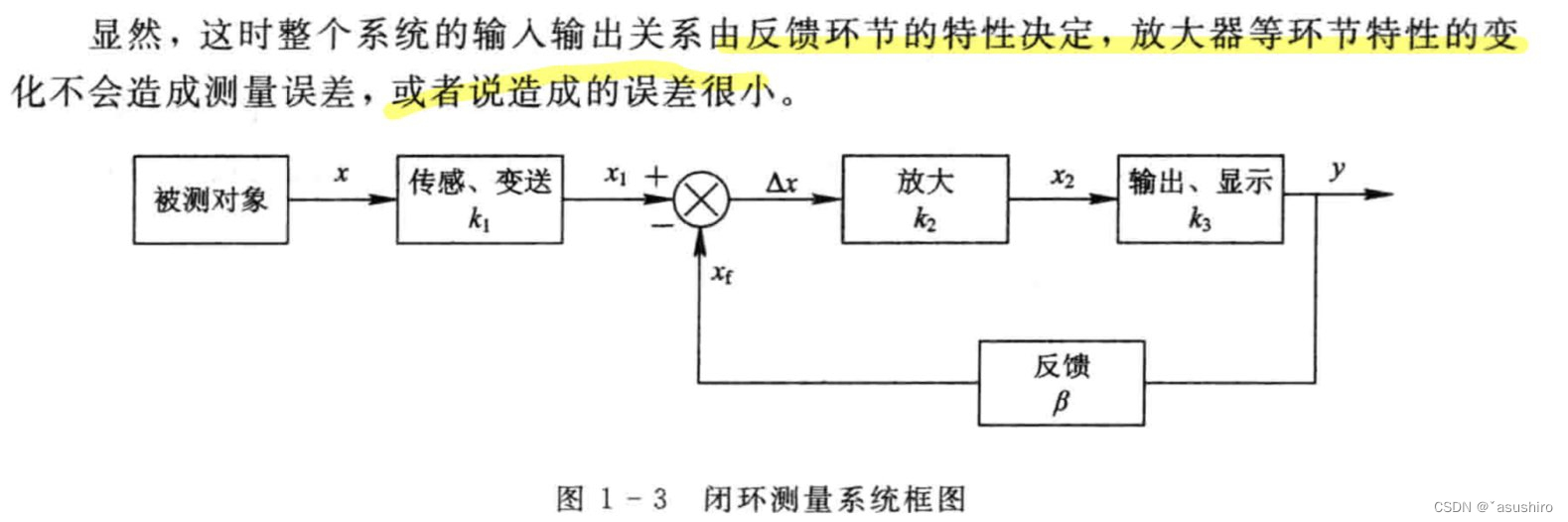
   闭环系统输入输出关系$$y=\frac{k_1}{\beta }x$$

区别：开环系统没有反馈，闭环系统有反馈

测量误差

表示方法

1. 绝对误差
   定义：测量值减真实值(真实值通常是约定的)
   $$\Delta =x?L$$

2. 相对误差
   定义：用绝对误差除以真值
   $$\delta =\frac{\Delta }{L}?100\%$$

3. 引用误差
   定义：用绝对误差除以（仪器测量范围的上限减测量范围的下限）
   $$\gamma =\frac{\Delta }{测量范围上限?测量范围下限}$$

误差的性质

1. 随机误差
   在同一测量条件下，多次测量被测量时，其绝对值和符号以不可预订方式变化着的误差，要按照统计规律进行处理如求均值
   随机误差的影响因素：电磁场的微变、零件的摩擦、间隙、热起伏、空气扰动、气压及湿度的变化等属于随机误差
2. 系统误差
   在条件发生改变时，按一定规律（如线性、多项式、周期性等函数规律）变化的误差，可以进行修正
3. 粗大误差
   超出规定条件下预期的误差，数据处理时要进行剔除
   
   例题1-3 用测量范围为-50~150kPa的压力传感器测量140kPa压力时，传感器测得示值为142kPa，求该示值的绝对误差、实际相对误差、引用误差。
   
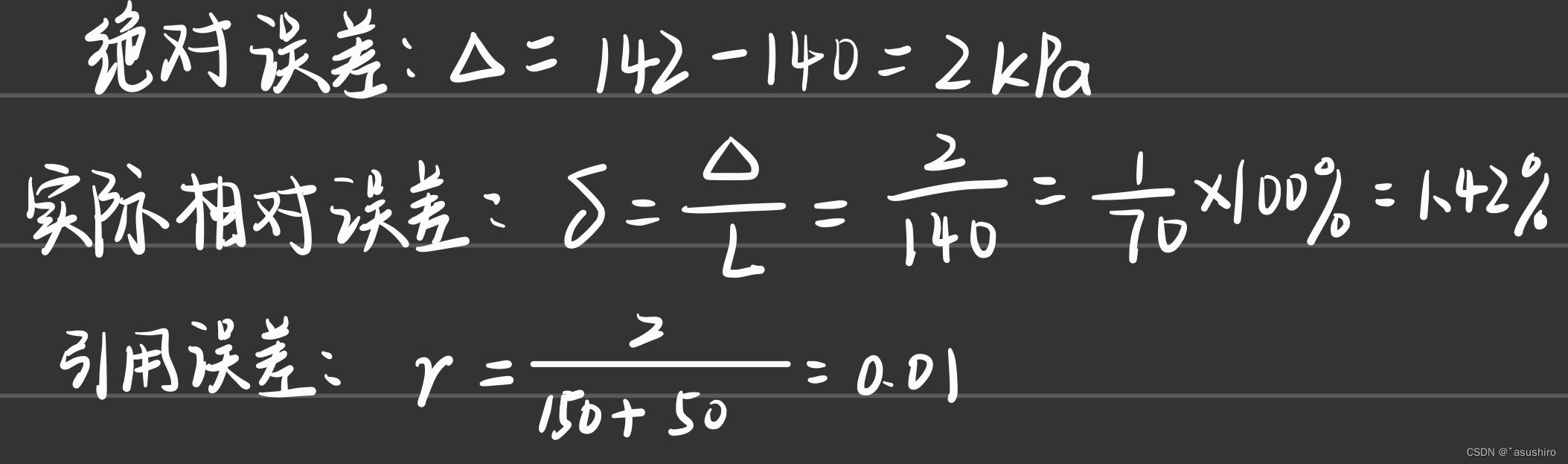
   例题1-5 已知待测力为70N,现有两只测力仪表，一只测量范围为0~500N，精度为0.5级，另一只测量范围为0 ~ 100N，精度为1.0级。问选用哪一只测力仪表好？为什么？
   

误差的处理
随机误差的处理
随机误差是服从正太分布的
特点：

1. 单峰性：越接近波峰出现的概率越大
2. 有界性：随机误差的绝对值不会超过一定界限（$3\sigma$准则等）
3. 对称性
4. 抵偿性

方法：

1. 算术平均值$\bar{x}$
   利用各个随机误差的算术平均值 $\bar{x}=\frac{1}{n}\sum x_i$ 作为真实值
   这样算出来的误差 $v_i=x_i?\bar{x}$ 对应的每一个，称为残差
2. 标准偏差
   由于真值实际上时拿不到的，所以我们要使用样本标准差，这两种的计算公式是不同的
   样本标准差$${\sigma }_s=\sqrt{\frac{1}{n?1}?(\sum x_i?\bar{x}{)}^2}=\sqrt{\frac{\sum v_i^2}{n?1}}$$
   算术平均值的可靠性指标用算术平均值的标准差${\sigma }_{\bar{x}}$来评定
   表示方法：$${\sigma }_{\bar{x}}=\frac{{\sigma }_s}{\sqrt{n}}$$
   因为平均值的标准差比单个数更小所以除了一个$\sqrt{n}$
3. 正太分布随机误差的概率处理
   可以认为绝对值大于 $3\sigma$ 的误差是不可能的，通常把这个误差称为极限误差
   测量结果可表示为$$x=\bar{x}+3{\sigma }_{\bar{x}}(p_a=0.9973)$$
   后面括号是置信区间
   
   

不等精度的直接层测量的权和误差
权可理解为各组测量结果相对的可信赖程度
权值的确定方法：一种方法是根据测量的次数，一种是根据标准差平方的倒数

粗大误差的处理：
方法是进行剔除
寻找的方法：

• 3$\sigma$准则
  步骤：
  1. 先算出$\sigma$, 将不在3$\sigma$内的点剔除掉
  2. 重新计算剩下的$\sigma$，直到所有的点都在3$\sigma$内
• 肖维勒准则
  实验使用多少$\sigma$与实验的次数有关
  
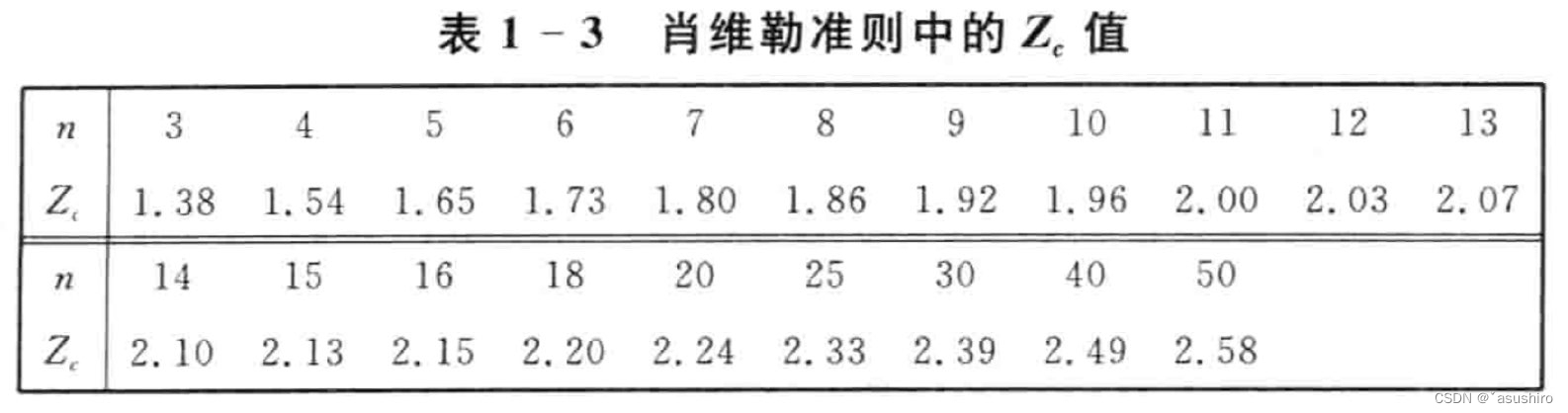
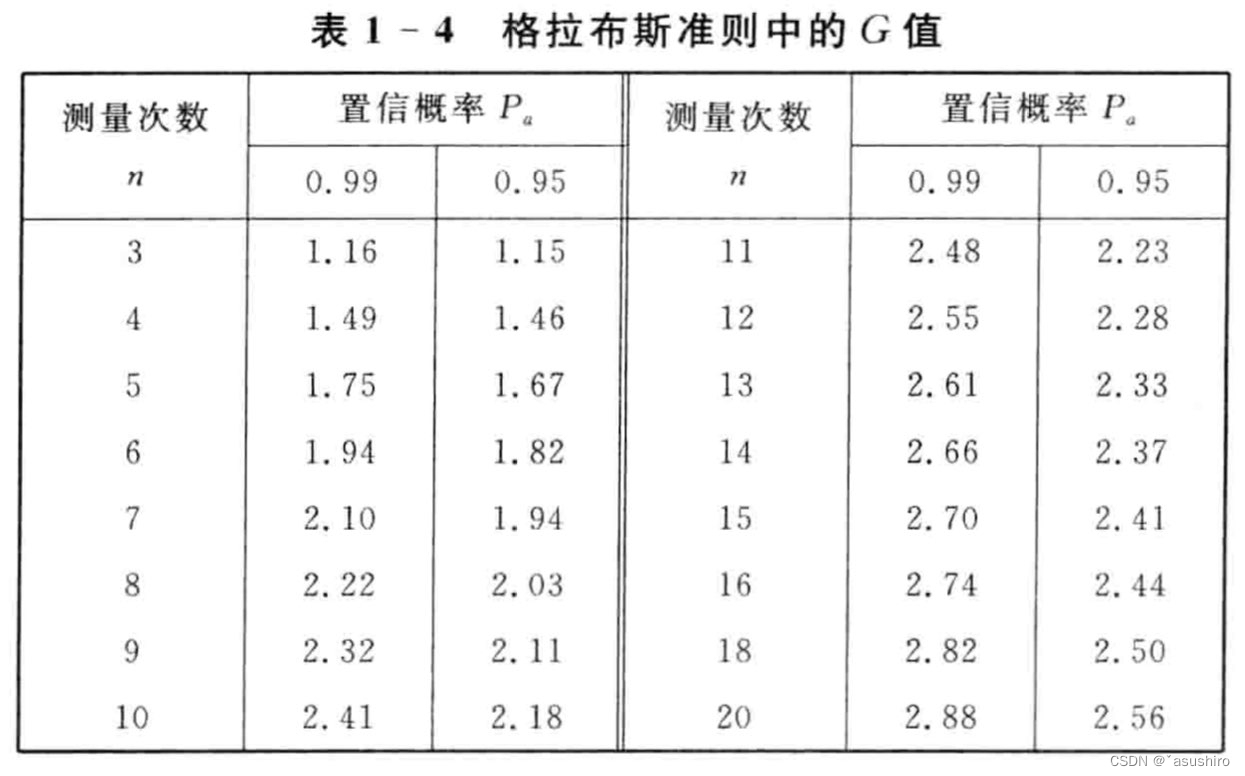
  对应多少$\sigma$如上表
• 格拉布准则
  格拉布给出了不同测量次数以及不同置信区间所需要多少$\sigma$
  

下一篇

未完待续