【深度视觉】第四章：卷积神经网络架构

六、卷积神经网络架构

前面给大家也详细展示了DNN的图像分类过程，一个最直观的感受就是图像数据太大，要设置巨量的神经元个数，算力根本就无法匹配，所以DNN只适合少量的数据，比如我们已经把图像数据卷积操作到变成48维向量了，然后再放入DNN是非常合适的。也所以卷积网络的卷积部分就是只要负责从图像数据中提取这48维特征向量即可。

而提取图像中的特征向量，从我给大家详细讲的卷积操作发展史和经典研究成果，就可以知道，就是一个设计卷积核组+某种统计操作的过程。于是这种卷积+池化+全连接(DNN)就是我们现在的卷积神经网络架构（Convolutional Neural Networks, CNN）的基本组成。

上图就是一个卷积神经网络架构：输入是一个三通道的彩色图片数据，经过卷积层CONV,就是用卷积核组提取特征的过程，经过激活层RELU就是进行非线性变换的过程，池化层POOL就是特征统计的过程，直到最后一层输出的就是一组向量，这组向量就是提取的输入图像的特征，然后这个向量送入FC全连接层进行分类。

所以一个典型的卷积网络一般都包含：
卷积层：负责提取特征的
激活层：负责非线性变换的，卷积是线性变换，激活层是进行非线性变换的
池化层：负责对提取的信息进行某些统计操作的
全连接层：负责分类任务的
当然以后遇到更复杂网络，还会有BN层、dropout等。

这里还要再强调一下就是：越靠前的卷积层提取的都是图像中细节的、局部的、纹理基元的信息；越往后面的卷积层它的感受野也就越大，它就相当于对前面卷积层提取的基元信息又进行了组合，提取的就是更大范围的、更粗颗粒的轮廓信息了。也所以从上图看，前面CONV层还有小汽车的全部信息，到后面的CONV层就是一团、一模的样子了，可能就是更高层的语义吧。

卷积的原理部分就这么多了，下面逐个详聊这些层的具体实现。

1、卷积层的工作原理

（1）当我们的图像数据是单通道数据、卷积核是一个卷积核时，我们的卷积操作是这样的：

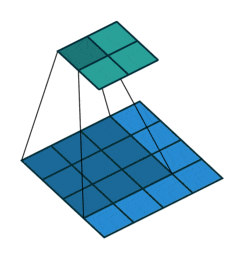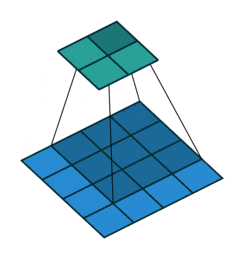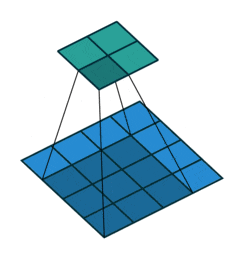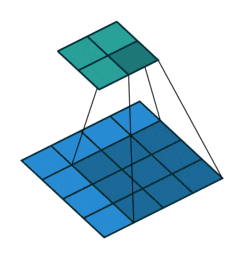
图中下层的图片就是图像数据，卷积核是一个3x3卷积核，用这个3x3的卷积核逐行逐列套到原图上，被套到的原图区域和卷积核进行卷积操作(对应位置相乘，然后全部数字相加)，结果放到上层图片的对应位置。这就是一次扫描操作。生成的对象就是上层的图片，这个图片叫特征图。

所以，用一个卷积核就可以对图像扫描一次。如果有多个卷积核，就可以对图像扫描多次。
扫描一次就生成一张特征图，扫描多次就生成多张特征图。

（2）当我们的图像数据是多个通道，我们扫描两次是这样的：

通常情况，我们卷积层的输入数据都是多通道的。上面以3通道为例，这种情况就是典型的第一层卷积层，因为第一层是原图数据喂入的，而原图数据一般都是三通道的彩图。

当我们喂入卷积层一个三通道的数据，就是上图的左列三张通道数据(input volume)。要扫描一次这三个通道数据，就需要3个不同的卷积核(Filter w0)。每个卷积核逐行逐列扫描自己对应的通道图，扫描完毕后就得到三张不同的特征图，然后把这三张特征图对应位置相加，再在每个元素上加一个偏置bias，此时生成的特征图就是上图右列的第一张结果图，也就是第一个特征图(output volume的第一张图)。

当我们再创建一组(这里就是3个，因为输入图是3通道的)卷积核组(就是中间的Filter w1)，再扫描一次输入数据，就生成第二张特征图,output volume的第二张特征图。

所以，当我们有多个通道的数据输入卷积层时，要想生成一张特征图，我们就得有通道个数个不同卷积核组，对输入进行扫描，扫描完毕后对应位置相加，最后再所有元素加偏置，就生成了一张特征。
当我们想生成多张特征图，我们就得用多个卷积核组进行扫描，才能得到多张特征图。

就是卷积核组的深度要和它要卷积的数据的深度要一致，这样才能卷积操作。一组卷积核组生成一张特征图。你想生成多张特征图，就得使用多组卷积核组。

2、pytorch中实现卷积层的类

pytorch把网络的一些基本架构都放在nn.Module类里面，所以卷积层也可以从这个模块里面调用：
CLASS torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1,bias=True, padding_mode='zeros')
必填参数：
in_channels：卷积层的输入。是输入卷积层的图像的通道数或上一层传入本层特征图的数量。
out_channels：卷积层的输出。是本层卷积层输出的特征图的数量。
kernel_size：卷积核的尺寸。无默认值必填。在实例化nn.Conv2d时就必须要写这个参数。参数可输入整数或者数组，输入整数代表卷积核的形状为正方形，输入数组代表卷积核的形状与数组一致。
可选参数：
stride：步长。默认是1，可以设置为一个数组，比如stride=(2, 2),就是卷积核扫描特征图的时候横向纵向移动的步幅。
padding：填充。

（1）in_channels、out_channels、bias
假如我们输入卷积神经网络的数据是一张拥有三个通道的彩色图像，那么这些输入数据首先先被卷积层分开，即分成三份同样尺寸但数值不一样的三组通道数据；然后用相同尺寸但不同数值的三个卷积核分别对上面分开的三组数据进行分别卷积计算，然后得到三个尺寸一样的特征数据；然后再把这三个'新通道'对应位置的元素相 加，如果有偏置再加上一个偏置，形成一张新得特征图。

上面的过程就是对图像进行了一次扫描。这一次的扫描是用三个不同的卷积核对三组通道数据分别扫描。

所以，在一次扫描中，无论图像本身有几个通道，就会有几个同尺寸不同数值的卷积核组去卷积全部通道，卷积完毕后再将卷积结果加和为一张feature map(有bias再加bias), 所以，一次扫描生成一个feature map, 无关原始图像的通道数目是多少。

out_channels就是扫描次数，就是上述过程进行多少次。所以扫描几次就生成几张特征图。

所以，一个卷积层的卷积核的个数就是out_channels个卷积核组，一个卷积核组就是in_channels个卷积核。那一个卷积层的卷积核个数就是out_channels x in_channels。
也所以，一个卷积层的参数个数就是in_channels x out_channels x 卷积核里面的数值的个数 + out_channels（就是有out_channels个是偏置，如果没有偏置就不加最后这个数了）。

一个通道数据我们一般要用多个卷积核进行扫描提取特征，一般扫描100、200甚至300次都是常规操作。但是不能对不同的通道扫描不同的次数，就是说要扫描多少次就是全部的通道都扫描多少次。

（2）kernel_size：卷积核尺寸
如果你使用的是经典架构，那经典架构论文里的尺寸就是最好的尺寸。如果是自己写的神经网络，那么你的核尺寸要遵循下面几个惯例：

一是，卷积核几乎都是正方形。这条惯例是因为在我们以往的经典图像分类任务中，许多图像都被处理成正方形或者接近正方形的形状，比如fashion mnist, CIFAR, imagenet等，如果你的图像尺寸非常长或者非常宽，那你可以使用与原图尺寸比例一致的卷积核尺寸。

二是，卷积核尺寸最好是奇数。比如3x3，5x5，7x7，这是行业惯例，传统视觉认为这是为了让被扫描区域能够中心对称，这样无论经历过多少次卷积变换，都能够以正常比例还原图像，也就是从平移不变性的角度来说明奇数核的好处。

这里我们也做个小实验，看看奇数核是如何比偶数核更能保持平移不变性：

三是，根据我们前面讲的卷积操作发展史上看，卷积操作有结合性、交换性等性质，所以一个大卷积核的操作可以用两个小卷积核来实现，而这样的替代可以节省很多算力。

（3）stride 步长
默认是1，可以设置为一个数组，比如stride=(2, 2),就是卷积核扫描特征图的时候横向纵向移动的步幅。
一是，设置步长可以调整模型的计算量，步长长了就可以加速扫描，并且降低扫描的不均衡性。步长为1也叫重叠扫描，重叠扫描时，越是中间的区域被扫描的次数就越多，也就是越是中间的像素，提取特征的次数越多。
二是，设置步长更重要的是可以实现大幅的数据降维，比如5x7的特征图，如果用3x3的扫描核，进行stride=1进行扫描，生成的特征图尺寸就是3x5， 如果用stride=2进行扫描，生成的特征图就是2x3,就相当于经过这一层卷积层后数据维度一下子从35降低到6。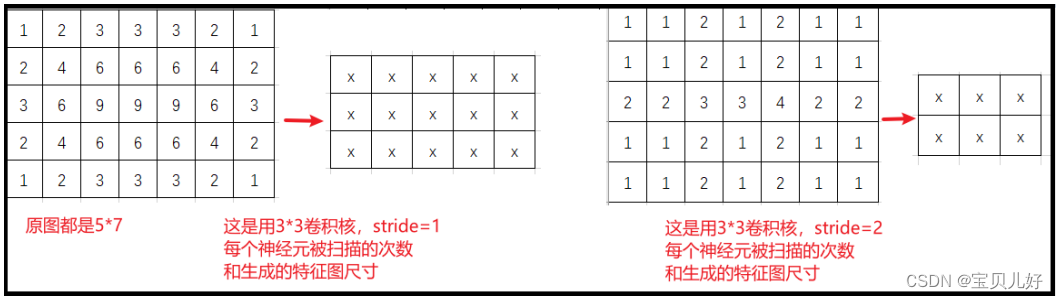

步长除了降低计算量，更重要的是会极大的影响特征图的输出尺寸。卷积网络里面的像素就是最小的特征单位，对图像数据来说一个像素格子就是一个神经元，所以，CV中说的降维就是指减少一张图像上的像素量。所以步长可以用来降维。
步长的设置一般都是1，2， 3三种情况。

（4）填充：padding、padding_mode
padding, 填充。之所以有padding是因为卷积前和卷积后的数据尺寸不一样，而且还存在扫描不完全或者扫描不均衡的情况。比如stride=3时，扫描到右边可能只剩2个或1个像素点了，此时就要抛弃这两个像素了，这就出现扫描不完全。比如stride=1时，边缘的像素只会被扫描1次，而中间的像素就会被扫描多次，就出现扫描不均衡，一般叫'中间重边缘轻'。

padding=1,表示在图像数据的外面填充一圈0，这样图像上原始像素就都被均衡的扫描了。
padding=2表示在图像数据外面填充2圈0.
padding=（2，3）表示横向填充2列，纵向填充3列，四个角也用0填满。
padding_mode='zeros'就是0填充，就是在图片填一圈黑框。
padding_mode='circular'是环形填充。
说明：
虽然有padding ，但是要使特征图每个像素都扫描到且扫描均衡，其影响因素不仅有padding,还有扫描核尺寸、步长的因素影响着，所以除了padding参数，我们还有valid模式和same模式。
‘VALID’= without padding, 就是没有扫描到的直接抛弃
‘SAME’ = with zero padding, 就是在有padding参数的情况下还是有扫描不到的像素，就自动在右边和下面继续加黑边直到被卷积核扫描到为止。

3、特征图尺寸的计算
特征图尺寸计算是非常重要的，尤其是你自己搭建网络时，你要非常清楚自己的输入是什么，输出是什么。
特征图尺寸对一个卷积神经网络而言非常重要，它既不能太大也不能太小。太小，进一步缩小的可能性就会降低，就会缺乏可以进一步提取信息的操作；网络深度就会受到限制，进而网络效果就会达到瓶颈。太大，每个卷积核需要扫描的次数就越多，卷积操作的计算量就会很大；此外，我们前面说过，卷积操作的目的是把原图像的信息压缩提取数据特征，图像数据经过卷积层后被提取的特征的数据的大小就是最后一个卷积层输出的feature map和这些feature map的数量(通道数)，然后我们将这些feature map的所有像素点拉平进入线性全连接层，所以在全连接层之前，我们能够从图像中提取多少信息就是我们的特征图的尺寸缩小到了什么样的水平，也就是原图图像整体像素缩小到了一个什么水平，而这个水平会严重影响卷积网络整体的预测效果和计算性能。所以特征图尺寸非常重要。

特征图尺寸计算通用公式：

通过这个公式，我们就可以设计我们的网络参数，让图像尺寸以我们想要的方式削减下去。

4、卷积网络中的数据流

我们先创建数据、搭建网络：
我创建数据的时候，本来是打算放一个小图片数据的，但是又一想，卷积层实例化后的参数都是随机生成的，所以卷积出来的结果也是随机的，可视化后也看不出什么规律，所以这里放一个非常简单的都是1的数据，给大家展示一下具体的计算流程：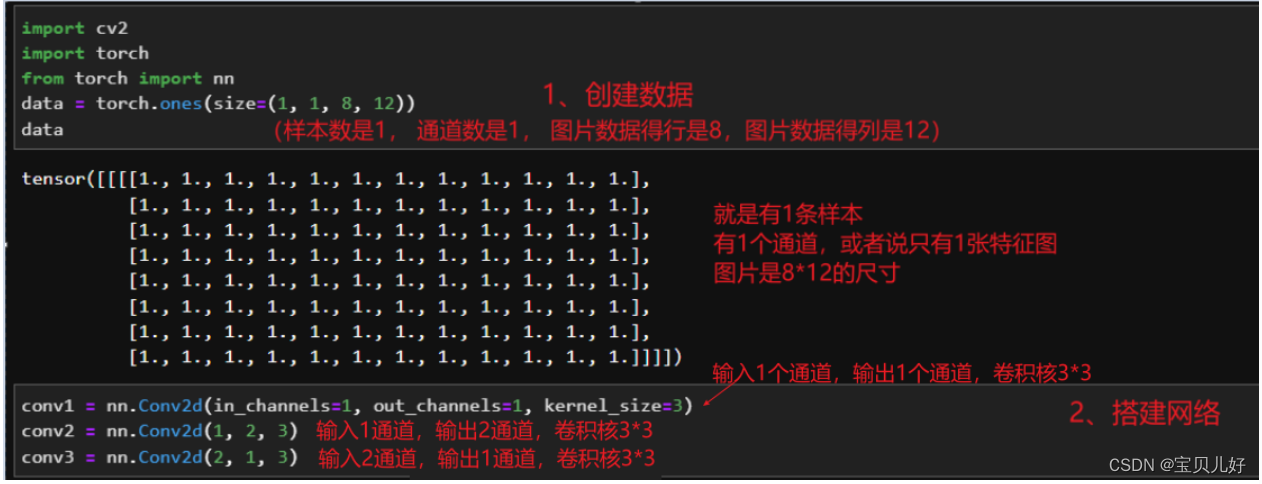

这里还是要强调一下数据，卷积网络的输入要求是三维tensor类型数据(通道数，行数，列数)或者是四维tensor类型(样本数,通道数,行数,列数)。当你的数据是三维的时候，意思就是你只喂入网络一张图片，而我们平时训练网络的时候都是大量的图片数据，所以都是按批次batch进行训练的，所以这里我们也都按四维数据结构输入网络。所以当你想喂入图像数据的时候，图像数据被cv2读出来后，你得先把结果reshape成(样本数，通道数，行数，列数)，才能喂入conv层。

我在搭建网络时，也是本着呈现数据是怎么计算的原则，所以，这里搭建的网络就非常简单，仅仅是展示一下数据流。第一个卷积层的输入是1，这个参数是根据样本数据的数据结构的，就是参数in_channels的值必须和(样本数，通道数，行数，列数)中的通道数保持一致，否则报错。参数out_channels就可以根据你自己的意愿设置，你可以设置128、256...等等都可以，你设置几就表示你打算扫描几次。这里是为了呈现数据流就扫描一遍，所以我的out_channels就设置为1。
第二个卷积层，它的输入是第一个卷积层的输出，所以它的输入也是1，这个层我让扫描2次，所以输出就是2，卷积核尺寸还设置为3x3
第三个卷积层，它的输入就是第二个卷积层的输出，所以输入是2。输出我这里设置1，就是只扫描一遍。
下面开始展示数据流动的过程：?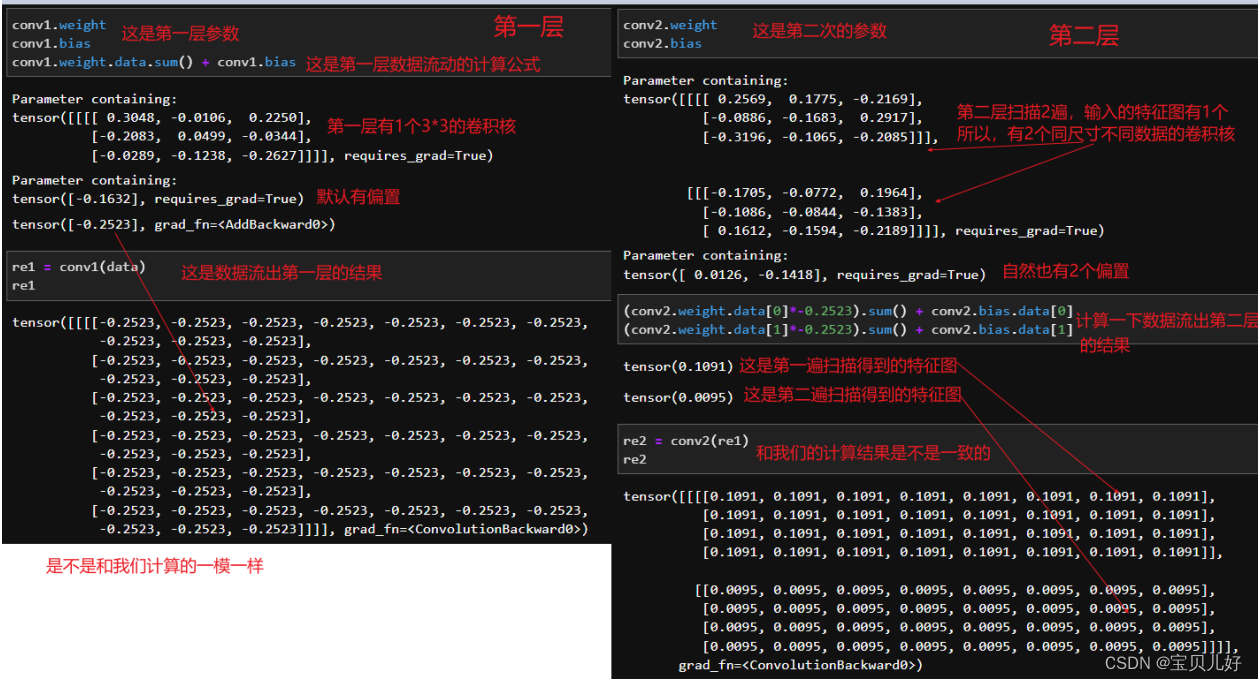

上面是分步的一个计算流程，下面看一下合并结果：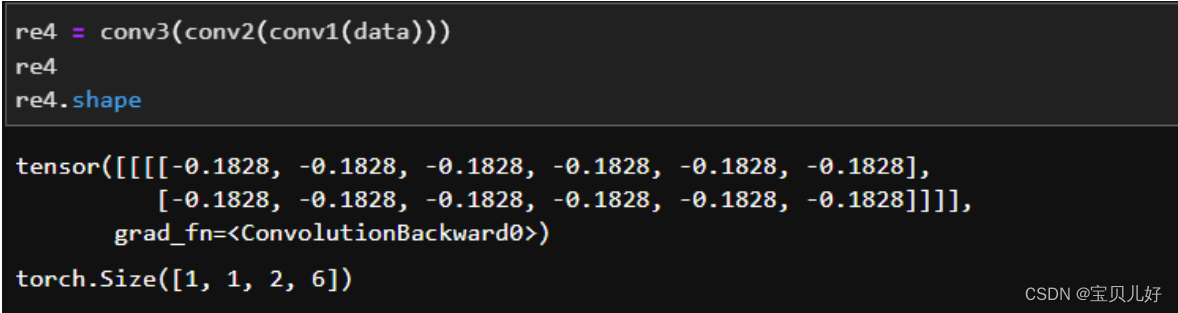

上面说过特征图的尺寸非常重要，借这个小例子，我们也梳理一下这里的特征图尺寸：
输入的尺寸：data.shape: torch.Size([1, 1, 8, 12]),这是我自己造的数据，我设置的就是8行12列
经过第一个卷积层：re1.shape：torch.Size([1, 1, 6, 10])，输出尺寸就是(h+2*padding- K)/stride + 1=(8-3)/1+1=6,同理12-3+1=10
经过第二个卷积层：re2.shape：torch.Size([1, 2, 4, 8]),这里padding都等于0，stride=1,K=3，所以不管是行还是列都是-3+1，即都-2
经过第三个卷积层：re3.shape：torch.Size([1, 1, 2, 6])

补充：一些奇妙的搭配：
kernal_size=3, padding=1,stride=1
kernal_size=5, padding=2,stride=1
kernal_size=7, padding=3,stride=1
....这些搭配图像输入输出的尺寸都不变！

我们还说过参数个数的计算也很重要，我们再梳理一下参数：每个层的参数是in_channels*out_channels个卷积核 + 偏置。
其中，卷积核的尺寸假如我们定的是3x3，那一个卷积核的参数就是9个。4x4卷积核对应的参数就是16个。
一个层要用多少个卷积核，这和这个层的输入in_channels和输出out_channels都有关。输入是1，输出是2，就需要2个卷积核。如果输入是2输出是1，也是需要2个卷积核。
一个层要用的偏置和这个层扫描的次数相关，或者说和生成的特征图数量有关，和输入无关！假如输入1输出是2就需要2个偏置。假如输入是2输出是1，那就需要1个偏置。偏置只和输出有关！

下面再展示一个图像尺寸变化过程的示例：?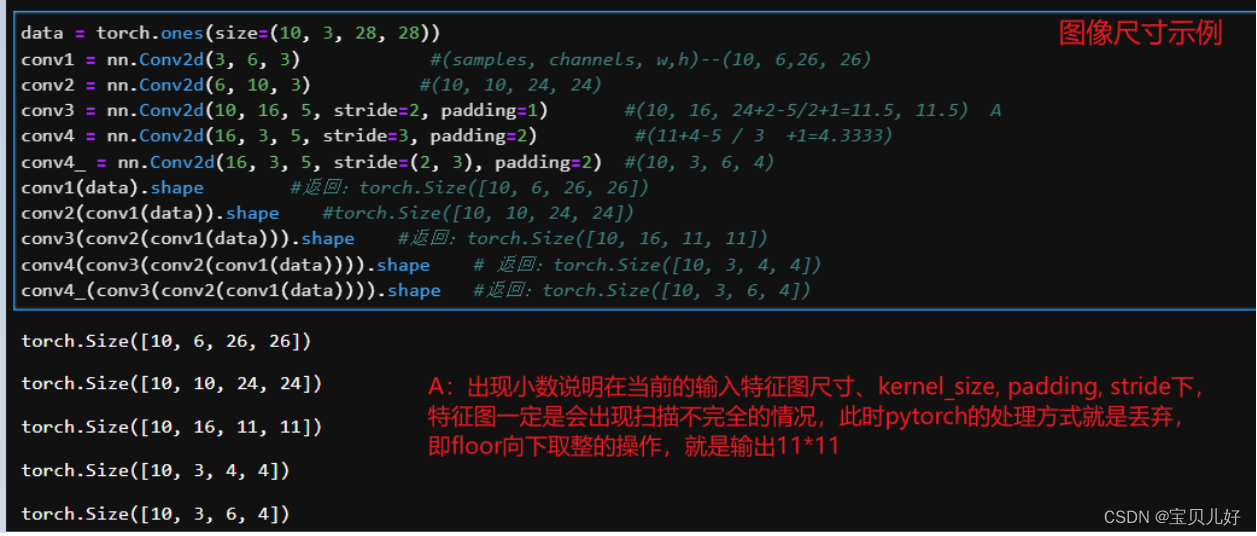

最后再说一下真实图像喂入卷积网络前的处理：?
强调这个点是因为，有的人上来就把源图像数据reshpe成4维，然后就喂入卷积层，我个人认为这样的做法非常不合适！因为卷积层是稀疏交互，也就是卷积核扫描的时候，提取的都是局部信息。而图片的局部信息，数据和数据之间的相对位置非常重要，不同的相对位置呈现出不同的人类视觉图像，所以最好不要轻易改变图片数字和数字之间的相对位置，不然肯定影响效果呀。所以一定不能暴力reshape,即使你不想分通道在stack，你可以用np.transpose()先调整通道再升维，而不是直接reshape到你想要的形状。
而且我们用reshape、view、squeeze、transpose、flatten或者切片时，我们一定要看好转化后的数据是不是你真正想要的变换。reshape和view在降维的时候，都是按通道降维，但升维就不一定了是你想要的方式了，所以一定要仔细查看。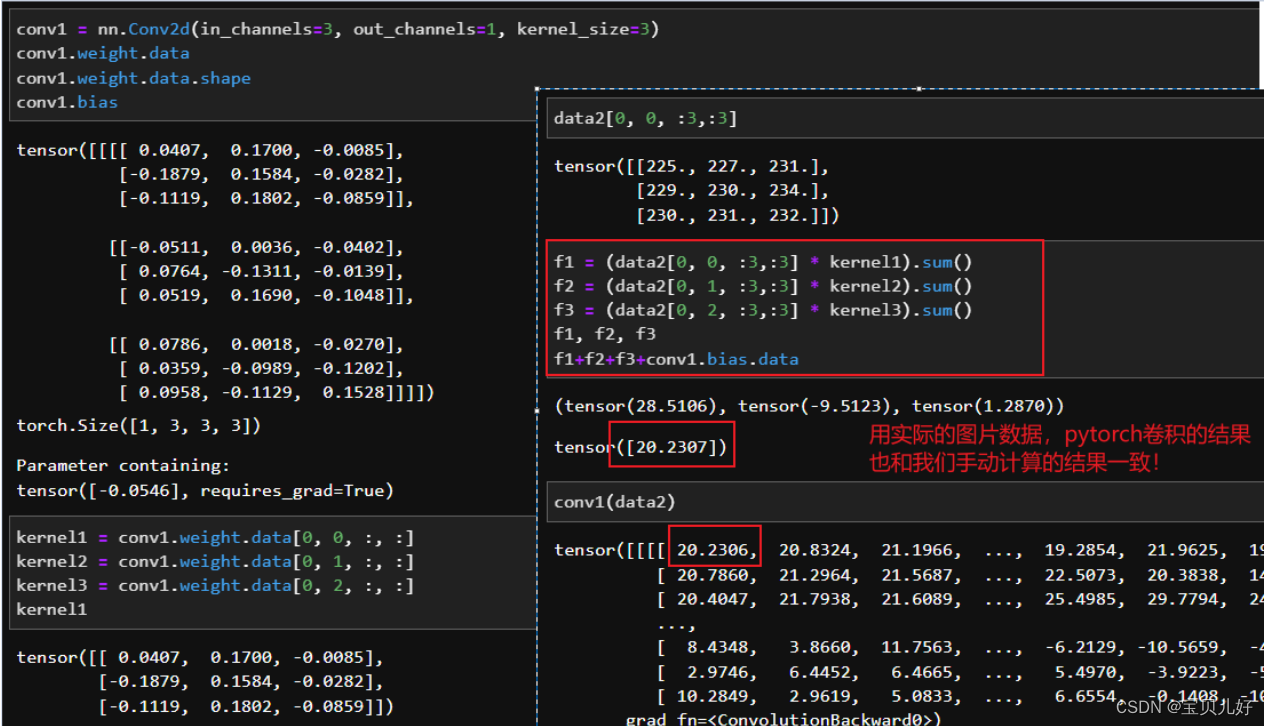

5、卷积操作底层的数学计算过程

我们上面讲卷积操作的过程，用一个卷积核套住对应区域->点乘->加和->移动->再点乘再加和再移动，一直到生成特征图所有元素值，这是让我们轻松理解卷积的计算过程的。其实在真实卷积计算中是直接用矩阵相乘即可，而且这样我还可以用显卡批量计算，一次指令就实现一次卷积操作，速度就大大提升了。我们看下面的例子来体会一下：

6、池化层 ： nn.MaxPool & nn.AvgPool

卷积神经网络里面的构成部分里面除了卷积层外最重要的组成部分就是池化层nn.MaxPool，它一般是跟在卷积层后面。
池化层是用来池化pooling操作的。我们之前讲卷积核组的时候，用了平均值来代替卷积结果，当时就说，这种操作就类似池化的效果。所以池化其实就是对卷积结果的一种统计操作。现在的卷积神经网络中池化层一般是对特征响应图各个小区域上指定一个值来代替这个小区域。这种统计操作后就直接减少了后续卷积层的参数的数量，降低计算开销，还可以防止过拟合。

常见的池化操作有最大池化max pooling, 平均池化average pooling，加和池化sum pooling这三种池化方式。
池化层也有池化核，但池化核只有核尺寸无核数据，一般都是2x2或者3x3的尺寸。
池化核扫描的过程和卷积层卷积核的扫描不太一样，池化核一般是不重叠的扫描，一般默认的都是最大池化扫描，就是扫描每个扫描野上的最大的那个数字作为一个像素输出到池化后的特征图的对应位置上的数字。
所以，池化层是不会改变通道的个数的，只会改变特征图尺寸的大小，所以说池化也是一种降维方式。
同理，平均池化和加和池化，就是把每个感受野的数字平均或者加和，这个平均或者加和的结果放到输出的特征图的对应位置上。
池化层是默认步长=池化核尺寸，这样不会重复扫描像素overlapping pooling, 即重叠池化，我们一般不做重叠池化是因为，池化的目的就是筛选一个个扫描野上最有特点的像素，把它拿出来作为我们的特征的，如果我们重叠池化就不能很好的达到这个目的了。而每个扫描野上哪个数字最有特点呢？那自然是最大的那个像素点 了，因为那个最大像素点，就说明以它为中心的那个区域的纹理，就是最匹配前面卷积核的纹理的区域，就是响应卷积核最大的区域，不就正是卷积核提取的信息嘛，那现在我们正好把这个信息拿出来即可。反过来，数值越小的点说明以那个像素点为中心的区域越不可能是卷积核提取的纹理特征。也所以我们为什么经常用最大池化操作。也类似于非最大化抑制，就是用最大的数值代表即可，非最大值就不用要了。就是保留对前面卷积核响应最强的值，响应不强的就丢掉。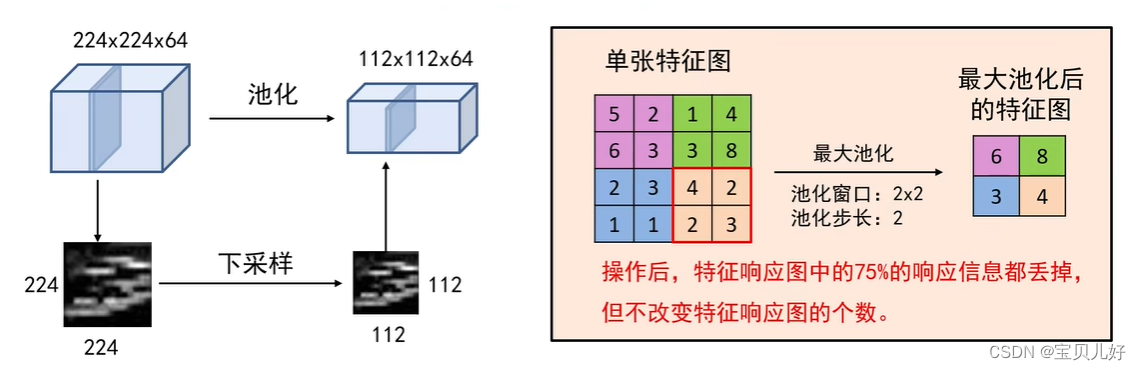

pytorch中的nn.module下面的pooling layer里面有maxpool1d, maxpool2d, maxpool3d, MaxUnpool1d(计算maxpool1d的局部逆),MaxUnpool2d,空间金字塔池化spatial pyramid pooling ,,,,,等等很多
class torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False,ceil_mode=False) 是要填写核尺寸一个参数即可，默认步长=池化核尺寸

说明池化层不改变样本量和通道数，但把特征图尺寸直接折半了。所以，当使用池化层时，我们最关心的就是输出的特征图的尺寸。我们一般将池化层作为一个缩小特征的一个工具来使用，所以pytorch提供一个类adaptive类，使用这个类，我们只要输入我们希望得到的输出尺寸就可以自适应来执行池化操作得到我们想要的尺寸。
class torch.nn.AdaptiveMaxPool2d(output_size, return_indices=False)
class torch.nn.AdaptiveAvgPool2d(output_size)
这两个类，我们只要输入output_size,池化层就可以自动帮助我们将特征图进行裁剪。

另外，池化层所有的参数都是超参数，不涉及任何可以学习的参数，所以增加池化层不会增加参数量。

7、BN层
前面讲DNN时详细讲过BN，那时我们用的BN是：
self.linear1 = nn.Linear(in_features, n_hidden, bias=bias)
self.normalize1 = nn.BatchNorm1d(n_hidden, momentum=momentum)
而卷积网络主要处理图像数据，所以用的类是：
class torch.nn.BatchNormal2d(num_features, eps=1e-05, momentum=0.1, affine=True,track_running_stats=True)
BN2d需要输入的数据是四维数据(第一个维度是samples),需要填写的参数只有num_features.
对卷积网络来说，是以特征图为单位来进行归一化的。所以BN层出现在卷积层的前后时，要输入的参数就只是前面层输出的特征图的数量。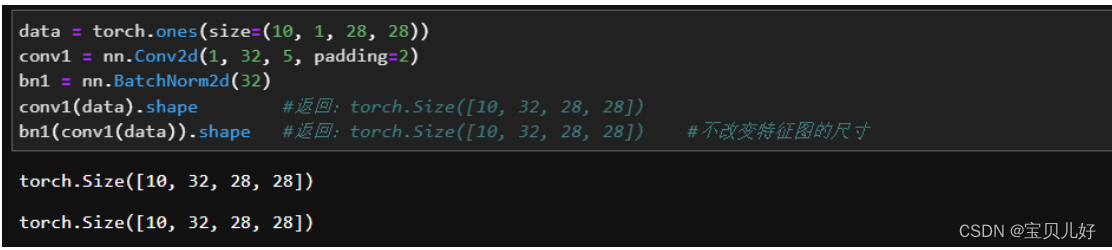

BN层的参数计算：一次BN化就要有γ 和 β两个参数，BN归一化是对每张特征图进行的归一化的，所以，归一化使用的参数就是：特征图的数量*2

8、Dropout层
Dropout就是随机失活。

随机失活：让隐藏层的神经元以一定的概率不被激活。
实现方式：在训练过程中，对某一层使用Dropout，就是随机将该层的一些输出舍弃(就是让输出值暴力置为0)，那这些被舍弃的神经元就好像被网络删除了一样。
随机失活比率(Dropout ratio)：是被设为0的特征所占的比例，通常在0.2-0.5范围内。
例如下图就是0.4的失活操作：

上面操作是每次正向传播时，该层的神经元都会有40%的概率被失活。所以每次正向传播，失活的神经元都不一样，而且失活的神经元个数也不一定，因为是概率嘛。

上面是DNN中的随机失活，在CNN中也一样，只是随机失活的是一定比率的特征图。CNN中的dropout2d，只需要输入一个参数P,但是在卷积网络里面，dropout层一次性是毙掉一个通道，也就是一张特征图，当特征图总数不是很多的时候，使用dropout的p值不会太大，否则会让CNN失去学习能力，造成欠拟合。所以p一般都是0.2， 0.25， 0.45， 0.55， 一般不会超过0.6，不然就是影响模型的学习能力了。
通常，使用dropout之后模型需要更多的迭代才能够收敛。
class torch.nn.Dropout2d(p=0.5, inplace=False)

虽然.shape返回的结果都相同，但是具体的数据是不同的，第二个数据有一半的数据都是0。
dropout层本身不带有任何需要学习的参数，因此不会影响参数量。

和DNN中的dropout层一样，CNN中的dropout层也是在模型训练的时候以一定的概率毙掉部分特征图，而模型一旦调到了测试模式，就也不会dropout了，而是所有输出特征图都*p往前传播了。当然，如果我们不用自己手写dropout层，都调用pytorch中已经打包好的层，我们是不用考虑这些因素的。