2024.1.6 关于 Redis 数据类型 Zset 常用命令

Set（集合）

元素具有唯一性
元素顺序无关紧要

实例理解

Set 类型?[1，2，3]?和 [2，1，3] 为同一个集合

List （列表）

元素具有唯一性
元素具有有序性，强调元素顺序十分重要

实例理解

List 类型 [1，2，3]?和 [2，1，3] 为两个不同的列表

Zset（有序集合）

元素具有唯一性
元素具有有序性，强调的是升序或降序

排序规则

Zset 中的 member 引入了?分数（score）浮点类型，形如（member - score）
即每个 member 都会安排一个分数（score），并按照各自?score 的大小进行?升序排序
我们通常将（member - score）称为一个 pair

实例理解

注意：

Zset 中的元素（member）具有唯一性，但分数（score）可重复
Zset 的主要作用为存储?元素（member）
即分数（score）仅作为?元素（member）在有序集合 Zset?中排序位次的参考依据

表格总结

数据结构 是否允许重复元素 是否有序 有序依据 应用场景
列表是是 索引下标 时间轴、消息队列
集合否否 标签、社交
有序集合 否是分数 排行榜系统

Zset 命令操作?

ZADD

用于向 zset 中添加元素（member）和分数（score）

注意：

不要把?member 和 score 理解成 "键值对" ，即（key - value）
键值对?具有明确的角色区分，即?谁是键谁是值是已经明确好了的，一定是根据键（key）来查到值（value）
而对于有序集合来说，既可以通过 member 找到对应的 score 又可以通过 score 找到相匹配的 member

语法：
zadd key [NX | XX] [GT | LT] [CH] [INCR] score member [score member ...]
[NX | XX]?

XX：只更新已存在元素，不添加新元素
NX：只添加新元素，不更新已存在元素

[GT | LT]

LT：只更新已存在元素，且当新设置的分数小于旧分数时才会更新，不阻止添加新元素
GT：表示只更新存在的元素，且当新设置的分数大于旧分数时才会更新，不阻止添加新元素

[CH]

描述了 zadd 命令的返回值
默认 zadd 命令返回?新增元素的个数
当添加 CH 选项后，zadd 命令返回新增元素 +?修改元素的个数

[INCR]

添加该选项，zadd 命令将如同 zincrby 命令
添加该选项后，此时的 zadd 命令只能指定一对（element - score）

时间复杂度：

对于添加的每一项来说，其时间复杂度均为 O(logN)
N 为有序集合中的元素个数

注意：

由于 zset 采用了跳表作为其内部数据结构
新增元素时按照元素自身的分数插入到相应位置
这样的设计使得在进行插入操作时，充分利用了跳表的有序性
因而将时间复杂度优化为?O(logN) ?而不是?O(N)

重点理解：

如果多个元素具有相同的分数，此时便会按照字典序进行排列
当然按分数排列仍让是放在首位的

ZRANGE

用于返回指定区间里的元素，按照分数升序遍历

语法：
zrange key start stop [withscores]
类似于 lrange 可以指定一对下标构成的区间，即 [start,stop] 区间
添加 withscores 选项，可以在返回时把分数也带上

注意：

有序集合本身元素就是有先后顺序的谁在前谁在后，都是很明确的！
因此也就可以给这个有序集合赋予下标这样的概念了

时间复杂度：

O(logN + M)
先根据 start 下标找到边界元素，再进行遍历操作
N 为有序集合中的元素个数
M 为下标 start 到 stop 之间的元素个数?

实例理解

我们利用 zrange 命令，来结合理解?zadd 命令

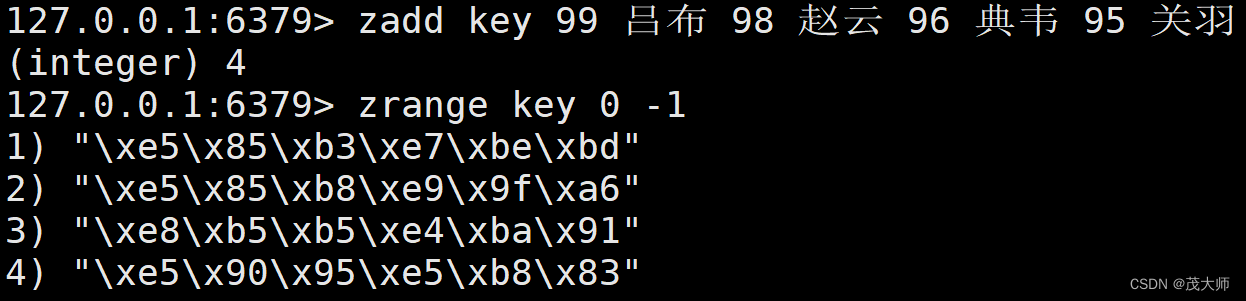
此处我们利用 zadd 命令向有序集合中添加若干 pair

Redis 内部存储数据时，是按照二进制的方式来进行存储的
这就意味着 Redis 服务器并不负责字符的编码?
所以要把二进制字节对应回汉字，需利用客户端来提供支持
我们在启动 Redis 客户端时，添加上后缀 "--raw" 即可

此处我们利用 zadd 命令来修改指定元素的分数

修改完分数后，还需对该元素进行重新排序，以此来维持有序序列的升序顺序

关于 zadd 命令选项?[NX | XX]?

关于 zadd 命令选项 [CH]

关于 zadd 命令选项 [INCR]

ZREVRANGE

用于返回指定区间里的元素，按照分数降序进行遍历
reverse ——> 逆序

语法：
zrevrange key start stop [withscores]
时间复杂度：

O(logN + M)
N 为有序集合中的元素个数
M 为下标 start 到 stop 之间的元素个数?

实例理解

此处的区间，两个参数的顺序是无需变换！

ZCARD

用于获取指定 zset 的元素个数

语法：
zcard key
时间复杂度：

O(1)

返回值：

指定 zset 中的元素个数

实例理解

ZCOUNT

用于?返回分数在 min 和 max 之间的元素个数

?语法：
zcount key min max 
默认为闭区间，即 [min,max]
如果想排除边界值，可以加上括号 "("

补充：

min 和 max 可以写成浮点数，因为 zset 的分数（score）本身就是浮点数?
在浮点数中存在两个特殊的数值

inf：无穷大（+∞）
-inf：负无穷大（-∞）

zcount?中分数也是支持使用 inf 和 -inf 作为 max 和 min 的！

注意：

此处的负无穷大不是指的无穷小！
无穷小是无限趋近于 0 的数值，而负无穷大的绝对值等于?无穷大

时间复杂度：

O(logN)

返回值：

满足条件的元素个数

重点理解：

zcount 指定分数区间 [min,max]
先根据 min 找到对应的元素，再根据 max 找到对应的元素，时间复杂度为?O(logN)

问题：

如果再进行一个遍历，是不是就知道 [min,max] 区间里的元素个数了呢？
那么此时的时间复杂度将为?O(M + logN)
其中 M 为区间中元素个数，N 为整个有序集合的元素个数

回答：

实际上 zset 内部会记录每个元素当前的次序
查询到元素，便可以直接知道该元素所在的次序
直接利用?max 对应的元素次序和 min 对应的元素次序相减再 +1
由此我们便可以 O(1) 的代价知道 min 和 max 之间的元素个数
并非是通过遍历的方式！！
所以此处 zcount 命令的时间复杂度为 O(logN)

实例理解

注意：

此处排除边界值的表示比较奇葩，需重点注意！

ZRANGEBYSCORE

用来返回指定分数区间里的元素
与 zcount 命令相似，只不过 zcount 返回的是指定分数区间的元素个数
zrangebyscore key min max [withscores]
时间复杂度：

O（M + logN）
N 为有序集合中的元素个数
M 为分数 min 到 max?之间的元素个数?

实例理解

注意：

该命令在 6.2.0 之后废弃，且该命令功能被合并到 zrange 命令中

ZPOPMAX

用于删除并返回分数最高的 count 个元素

语法：
zpopmax key [count]
时间复杂度：

O(M * logN)
N 为?有序集合中的元素个数
M 为 count 值，即要删除的元素个数

返回值：

被删除的元素（包括 member 和 score）

重点理解：

zpopmax 命令删除的是有序集合的最大值，其最大值就相当于末尾元素，也就相当于尾删

问题一：

既然是尾删，为什么不把末尾元素的特殊位置给记录下来？
后续如果需要删除的话，其时间复杂度不就可以为 O(1) 了嘛？还省去了查找的过程！
O(logN) ——> O(1)

回答：

这个事是有可能的！
但是很遗憾，Redis 并没有这么做
事实上，Redis 的源码中，针对有序集合，确实是记录了尾部这样的特殊位置
但是实际删除的时候，并没有用到这个特性，而是直接调用了一个通用的删除函数，即给定一个 member 的值，进行查找到位置之后再删除
此处我认为是存在优化空间的！

问题二：

虽然存在这样的优化空间，但是未来会真的优化吗？

回答：

也不好说
优化这种活，要优化到刀刃上！
优化一般是要先找到性能瓶颈，再针对性能优化！
因为当前的这个 O(logN) 的速度其实是不慢的！
如果 N 不是非常夸张的大，基本是可以近似看作O(1)的

实例理解

此处类似于 top K?问题

如果存在多个元素分数相同，且同时为最大元素时，zpopmax 命令仍然只删除其中的一个元素！
虽然分数是主要因素，但如果分数相同仍会按照 member 字符串的字典序决定先后！

BZPOPMAX?

ZPOPMAX?命令的阻塞版本

注意：

blist 和 brpop 这两个命令是针对 List ，实现类似于阻塞队列的效果
咱们这里的有序集合也可以视为是一个优先级队列?
有时候也需要一个带有阻塞功能的优先级队列

语法：
bzpopmax key [key ...] timeout 
每个 key 均对应一个有序集合
阻塞也是在有序集合为空的时候触发阻塞，阻塞到有其他客户端插入元素为止
timeout 代表超时时间，即最多阻塞多久，单位为?秒且支持小数形式

时间复杂度：

O(logN)

返回值：

被删除的元素（包括 member 和 score）

问题：

如果当前 bzpopmax 命令同时监听了多个 key，假设 key 是 M 个
此时时间复杂度是 O(M * logN) 吗？

回答：

不是！
啥时候才需要 * M ？
即每个这样的 key 上面都删除一次最大元素！
而当 zpopmax 命令同时监听多个 key 时，哪个 key 对应的有序集合最快插入元素，便删除该 key 对应有序集合的最大值！?

实例理解

当然如果有序集合中已经有了元素，直接就能返回！不会进行阻塞了！

ZPOPMIN

用于删除并返回分数最低的 count 个元素

语法：
zpopmin key [count]
时间复杂度：

O(M * logN)
N 为?有序集合中的元素个数
M 为 count 值，即要删除的元素个数

返回值：

被删除的元素（包括 member 和 score）

注意：

zpopmin 和 zpopmax 命令的逻辑是一致的，即均由同一个函数实现

虽然 Redis 的有序集合记录了开头的位置，但是删除的时候使用的是通用的删除函数

导致出现了重新查找的过程

返回值：

被删除的元素（包括 member 和 score）

实例理解

BZPOPMIN

ZPOPMIN?命令的阻塞版本

语法：
bzpopmin key [key ...] timeout
用法和 bzpopmax 命令一样

时间复杂度：

O(logN)

返回值：

被删除的元素（包括 member 和 score）

实例理解

ZRANK

用于返回指定元素的下标，升序

注意：

zrank 命令得到的下标是从前往后算的，即升序

语法：
zrank key member
时间复杂度：

O(logN)
最主要是有一个查询位置的过程

返回值：

元素（member）对应的下标

实例理解

ZREVRANK

用于返回指定元素的下标，降序
rev ——> reverse

注意：

zrevrank 命令得到的下标是从后往钱算的，即降序

语法：
zrevrank key member
时间复杂度：

O(logN)

返回值：

元素（member）对应的下标

实例理解

ZSCORE

用于查询指定元素的分数

语法：
zscore key member
时间复杂度：

O(1)

重点理解：

上述介绍的命令，根据 member 查找元素，其时间复杂度均为 O(logN)
但是此处 Redis 对 zscore 命令这样的查询操作做了特殊优化
即付出额外的空间代价，但将时间复杂度优化到了 O(1)

返回值：

指定元素所对应的分数

实例理解

ZREM

用于删除指定的元素

语法：
zrem key member [member ...]
时间复杂度：

O(M * logN)
N 为整个有序集合中元素个数
M 为 member 的个数
因为此处的 member 不会有太多，也可认为是?O(logN)

返回值:

本次操作成功删除的元素个数

实例理解

ZREMRANGEBYRANK

用于删除指定下标范围的元素

语法：
zremrangebyrank key start stop
使用这个下标描述的范围进行删除，且范围为 [start,stop]

时间复杂度：

O(M + logN)
N 为有序集合中的元素个数
M 为 [start,stop] 区间的元素个数

注意：

此处查找位置，只需要进行一次，无需重复进行

返回值：

删除成功的元素个数

实例理解

ZREMRANGEBYSCORE

用于删除指定分数范围区间的元素

语法：
zremrangebyscore key min max
使用这个分数描述的范围进行删除，且范围为 [min,max]

时间复杂度：

O(M + logN)
N 为有序集合中的元素个数
M 为?[min,max]?区间中元素个数

返回值：

删除成功的元素个数

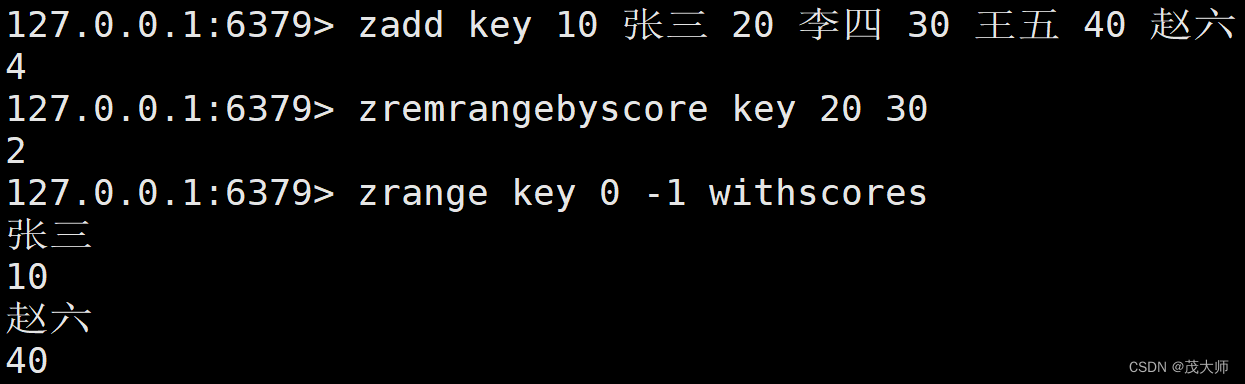
实例理解

ZINCRBY

用于为指定元素的关联分数添加指定的分数值

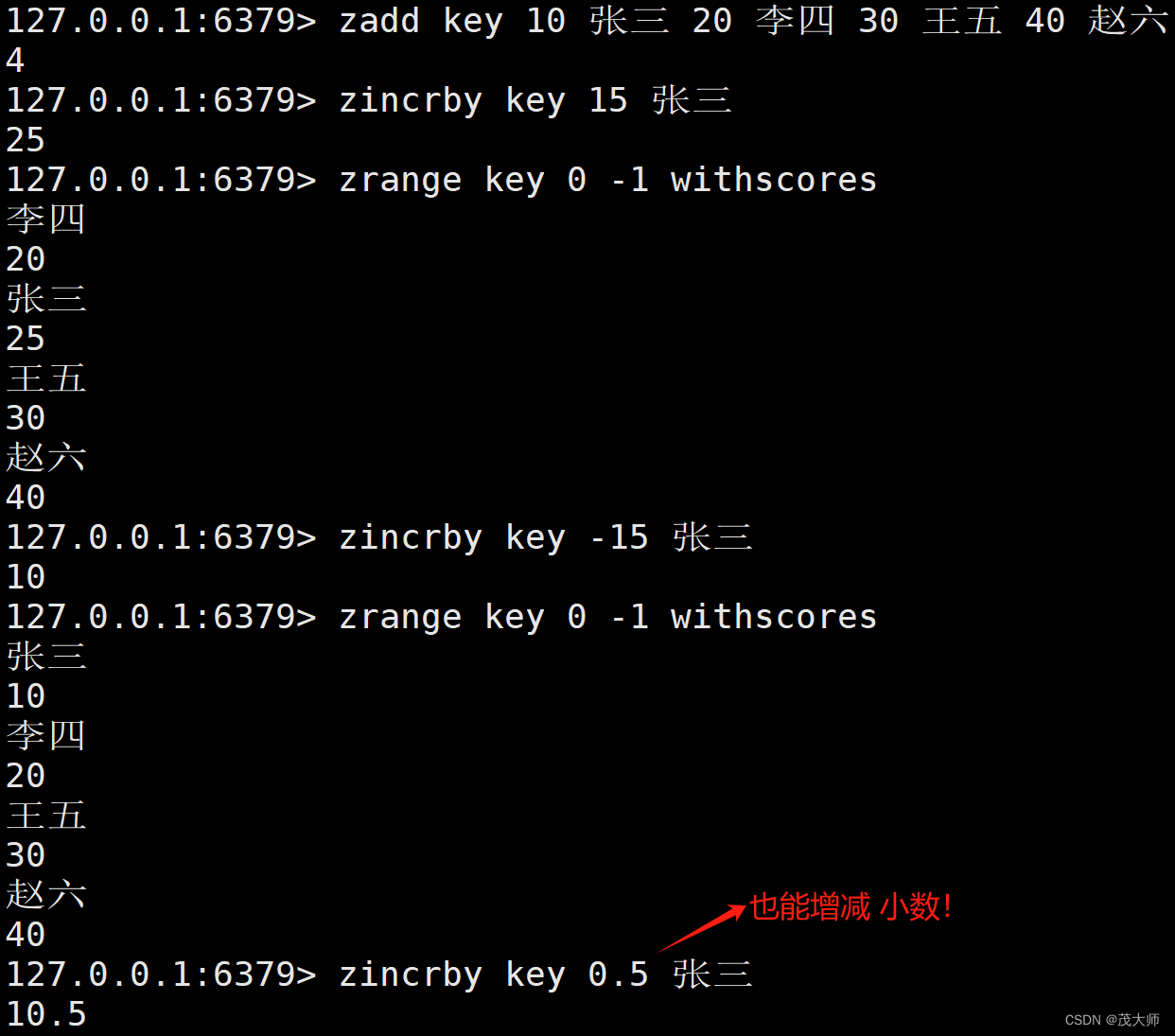
注意：

zincrby 命令不仅会修改分数内容，也会同时移动元素，来保持整个有序集合仍为升序

语法：
zincrby key increment member
时间复杂度：

O(logN)

返回值：

增加后元素的分数

实例理解

文章来源:https://blog.csdn.net/weixin_63888301/article/details/135328508
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

数据结构	是否允许重复元素	是否有序	有序依据	应用场景
列表	是	是	索引下标	时间轴、消息队列
集合	否	否		标签、社交
有序集合	否	是	分数	排行榜系统