回顾【数学基础】找出断层,继续前进, 使用chatGPT学习并解决实际问题:微积分
已经学过的算术、代数、几何。跳过。
从微积分开始
想象一下,你在画一条曲线,或者在一个大草地上奔跑。微积分就是一种数学工具,帮助我们了解这条曲线的形状,或者你奔跑的方式。
-
微分(就像研究曲线上的每一小点):
- 微分帮助我们了解某一瞬间的情况。比如,当你骑自行车时,你想知道你正好在某一点上的速度有多快。微分就可以告诉你这个。
- 就像用放大镜看曲线上的一个小点,微分告诉我们这个小点的信息,比如它是上坡还是下坡。
-
积分(就像把一小块一小块加起来):
- 积分是把很多小块加在一起,来了解整体的情况。比如,你想知道一段时间内你骑自行车走了多远,积分就可以帮你算出来。
- 如果你有一张被撕成很多小片的纸,积分就像是把这些小片重新拼回去,让你看到整张纸的样子。
所以,微积分就像是一个神奇的工具,可以告诉我们很多关于曲线和运动的信息。它可以帮助我们解决很多实际的问题,比如建造桥梁、设计过山车,甚至是预测天气。对于科学家和工程师来说,微积分就像是他们的超级工具箱!
微积分是数学的一个分支,主要研究函数、极限、导数、积分以及它们的应用。微积分的发展是为了解决两类主要问题:变化率(微分)和累积(积分)。
-
微分(Differential Calculus):
- 微分的核心是导数的概念。导数衡量的是一个量相对于另一个量变化的快慢,即变化率。
- 在物理学中,速度是位置对时间的导数,加速度是速度对时间的导数。
- 在经济学中,导数可以用来计算成本、收益或利润的变化率。
- 微分的概念被用于优化问题,比如找到成本或生产效率的最小值或最大值。
-
积分(Integral Calculus):
- 积分涉及累积量,它是微分的逆运算。积分可以用来计算面积、体积、位移等。
- 定积分可以用来确定曲线下的面积,这在物理学中用于计算物体在力的作用下移动的距离。
- 不定积分涉及到找到函数的反导数或原函数,这在解决物理学中的运动方程时非常重要。
微积分的理论和技术被广泛应用于科学、工程、经济学和许多其他领域。它是现代科学和工程的基石之一,是理解和描述自然界中连续变化的强有力工具。简而言之,微积分使我们能够更好地理解世界,解决实际问题,从构建桥梁和飞机到预测经济变化等。
让我们通过一个具体的例子来说明使用微积分和不使用微积分的区别。假设我们要解决的问题是设计一个水滑梯。
不使用微积分的情况:
- 如果我们不使用微积分,我们可能会根据经验或简单的准则来设计水滑梯。例如,我们可能会选择标准的坡度和曲线,不考虑滑梯上水流的速度变化或者人在滑梯上的确切运动路径。
- 这种方法可能会制造出一个基本功能的水滑梯,但可能无法优化乘坐体验,也可能在安全性方面存在缺陷。
使用微积分的情况:
- 使用微积分,我们可以精确计算滑梯的每一点上的坡度和曲率,以及人在滑梯上的速度和加速度。这涉及到微分的概念,帮助我们了解速度和加速度在任何给定点的变化。
- 我们还可以使用积分来计算整个滑梯的总长度,或者计算人在滑梯上的总体动能。这有助于我们确保水滑梯既刺激又安全。
- 此外,我们可以通过微积分来优化水流,确保水滑梯的表面始终有足够的水流,提供顺畅且安全的滑行体验。
总的来说,使用微积分可以让我们更精确地理解和控制水滑梯的设计。这不仅提高了乘坐的安全性和舒适性,还能确保滑梯的设计符合特定的技术和功能标准。相比之下,不使用微积分可能导致设计更加简化,可能无法充分考虑到所有的物理因素,从而影响最终产品的质量和安全性。
我们来看一个简单的例子:抛物线的轨迹。
不使用微积分,我们可以通过测量抛物线的不同位置的高度和距离,然后绘制出抛物线的图像。但是,这种方法比较繁琐,而且不易准确。
使用微积分,我们可以通过求抛物线的导数来计算抛物线的斜率。然后,我们可以使用斜率的定义来计算抛物线的高度和距离。这种方法更加简便,而且更容易准确。
具体的计算过程如下:
假设抛物线的方程为 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c。那么,抛物线的斜率为 y ′ = 2 a x + b y'=2ax+b y′=2ax+b。
我们可以求出 y ′ y' y′ 在 x = 0 x=0 x=0 处的值,也就是抛物线在 x = 0 x=0 x=0 处的斜率。
根据斜率的定义,我们可以计算出抛物线在 x = 0 x=0 x=0 处的高度和距离。
通过这种方法,我们可以很容易地计算出抛物线的轨迹。
以下是使用微积分和不使用微积分计算抛物线轨迹的对比表:
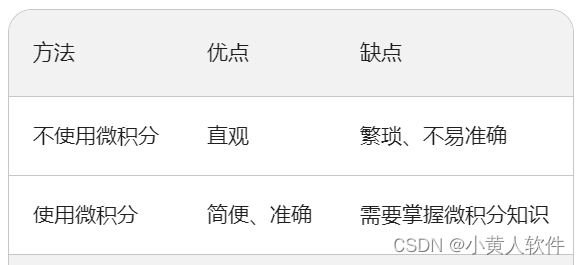
从这个例子可以看出,使用微积分可以使我们更容易、更准确地解决问题。
数学基础 主要领域的概述:
-
算术(Arithmetic):算术是数学的基础,涉及数字的基本运算,如加法、减法、乘法和除法。它还包括理解整数、分数和小数的概念。
-
代数(Algebra):代数介绍了变量和未知数的概念,以及如何处理这些数。基础代数包括解一元一次方程和一元二次方程,以及理解多项式、因式分解和代数表达式的概念。
-
几何(Geometry):几何涉及形状、尺寸、相对位置以及空间属性的研究。基础几何包括理解不同形状的属性(如线段、角、三角形、多边形、圆等)和计算它们的面积和体积。
-
三角学(Trigonometry):三角学是研究三角形和角度关系的数学分支。它涉及理解正弦、余弦、正切等三角函数,以及如何应用它们来解决问题。
-
概率论与统计(Probability and Statistics):这部分包括收集、分析、解释、展示和组织数据。概率论涉及预测事件发生的可能性,而统计则是关于数据的分析和解释。
-
微积分(Calculus):微积分是数学中的一个高级领域,涉及极限、导数、积分和无穷级数。它用于研究变化率和积累量。
-
离散数学(Discrete Mathematics):这是研究离散元素的数学领域,常用于计算机科学。包括逻辑、集合论、图论、数论等。
-
线性代数(Linear Algebra):线性代数涉及向量空间和线性方程组。它包括矩阵理论、向量、线性变换等概念。
这些主题构成了数学的核心基础,是进一步研究更复杂数学概念和应用的基石。不同领域之间存在重要的交叉点,共同构建了数学作为一个统一的学科。
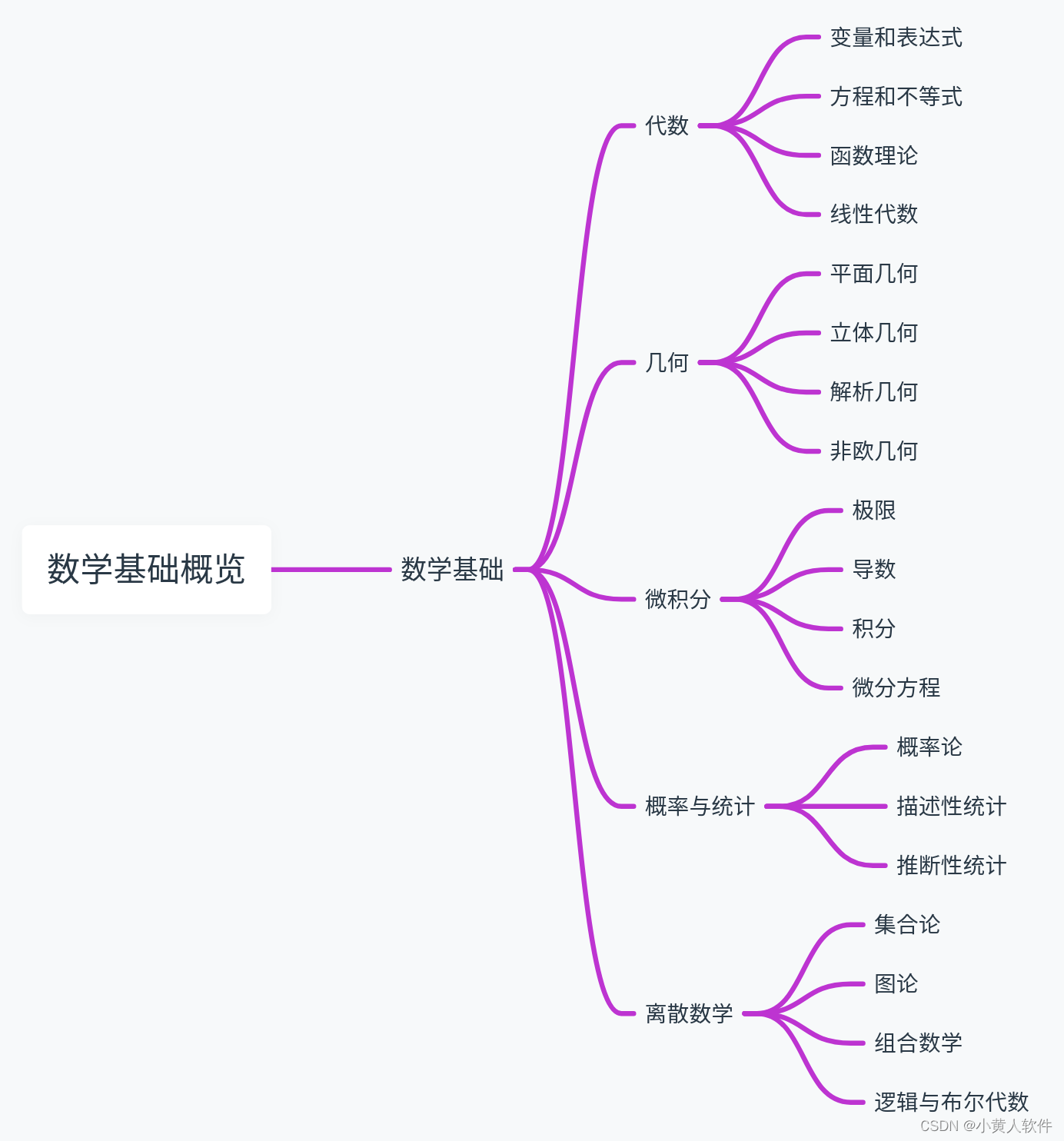
- 数学基础
- 代数
- 变量和表达式
- 方程和不等式
- 函数理论
- 线性代数
- 几何
- 平面几何
- 立体几何
- 解析几何
- 非欧几何
- 微积分
- 极限
- 导数
- 积分
- 微分方程
- 概率与统计
- 概率论
- 描述性统计
- 推断性统计
- 离散数学
- 集合论
- 图论
- 组合数学
- 逻辑与布尔代数
- 代数
数学的基础理论,包括数学逻辑、公理化集合论、数学分析、代数学、几何学等。这些理论为数学各分支学科提供了坚实的基础,并为数学的发展提供了源源不断的动力。
数学逻辑是研究逻辑推理和证明的理论。它是数学的基础,也是其他学科,如计算机科学、哲学、语言学等的基础。数学逻辑的主要内容包括命题逻辑、谓词逻辑、集合论逻辑、递归论等。
公理化集合论是研究集合的理论。它是现代数学的基础,是数学各分支学科的基础。公理化集合论的主要内容包括集合、子集、并集、交集、差集、补集、等价关系、函数等。
数学分析是研究实变数和复变数函数的理论。它是数学的重要分支,与许多学科都有密切联系,如物理学、化学、工程学、经济学等。数学分析的主要内容包括函数的极限、连续性、可导性、积分、微分方程等。
代数学是研究数和数的运算的理论。它是数学的重要分支,与许多学科都有密切联系,如物理学、化学、工程学、计算机科学等。代数学的主要内容包括整数、有理数、实数、复数、群、环、域、代数方程等。
几何学是研究图形、空间和它们之间的关系的理论。它是数学的重要分支,与许多学科都有密切联系,如物理学、化学、工程学等。几何学的主要内容包括点、线、面、体、空间、投影、几何体、几何形状等。
数学基础是数学的重要组成部分,是数学各分支学科的基础。它为数学的发展提供了坚实的理论基础,并为数学的研究提供了强有力的工具。
按层次:
基础:数学基础的基本概念和原理,包括数学符号、数学命题、数学推理、数学证明等。
初级:数学基础的基本知识和技能,包括算术、代数、几何等。
中级:数学基础的深入研究,包括数学逻辑、公理化集合论、数学分析、代数学、几何学等。
高级:数学基础的更深入研究,包括现代数学、数学哲学等。
数学基础是数学的基础知识,包括数学的基本概念、运算、公式、定理等。数学基础是学习其他数学分支的基础,也是解决实际问题的基础。
数学基础的内容主要包括以下几个方面:
- 数学基本概念:数、量、关系、函数、图形等。
- 数学基本运算:加、减、乘、除、求余、开方、对数等。
- 数学基本公式:勾股定理、毕达哥拉斯定理、面积公式、体积公式等。
- 数学基本定理:欧几里得公理、对偶定理、极值原理等。
数学基础的学习可以分为以下几个阶段:
- 初级阶段:学习数学的基本概念、运算、公式、定理等。
- 中级阶段:学习更高级的数学概念、运算、公式、定理等。
- 高级阶段:学习更抽象的数学概念、运算、公式、定理等。
数学基础的学习方法主要包括以下几个方面:
- 理解:理解数学的基本概念、运算、公式、定理等。
- 练习:通过练习巩固对数学基础知识的理解。
- 思考:通过思考提高对数学基础知识的理解。
数学基础的学习技巧主要包括以下几个方面:
- 多看书:多看数学书籍,了解数学基础知识。
- 多做题:多做数学题,巩固对数学基础知识的理解。
- 多思考:多思考数学问题,提高对数学基础知识的理解。
数学基础的学习意义主要包括以下几个方面:
- 为学习其他数学分支打下基础。
- 为解决实际问题打下基础。
- 提高思维能力、逻辑能力、解决问题的能力等。
数学基础的学习建议主要包括以下几个方面:
- 从基础开始:从数学的基本概念、运算、公式、定理等开始学习。
- 循序渐进:循序渐进地学习数学基础知识。
- 坚持不懈:坚持不懈地学习数学基础知识。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!