数据结构与算法教程，数据结构C语言版教程！（第三部分、栈(Stack)和队列(Queue)详解）四

?第三部分、栈(Stack)和队列(Queue)详解

栈和队列，严格意义上来说，也属于线性表，因为它们也都用于存储逻辑关系为 "一对一" 的数据，但由于它们比较特殊，因此将其单独作为一章，做重点讲解。

使用栈结构存储数据，讲究“先进后出”，即最先进栈的数据，最后出栈；使用队列存储数据，讲究 "先进先出"，即最先进队列的数据，也最先出队列。

既然栈和队列都属于线性表，根据线性表分为顺序表和链表的特点，栈也可分为顺序栈和链表，队列也分为顺序队列和链队列，这些内容都会在本章做详细讲解。

七、什么是队列（队列存储结构）

队列，和栈一样，也是一种对数据的"存"和"取"有严格要求的线性存储结构。

与栈结构不同的是，队列的两端都"开口"，要求数据只能从一端进，从另一端出，如图 1 所示：

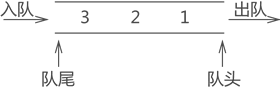
图 1 队列存储结构

通常，称进数据的一端为 "队尾"，出数据的一端为 "队头"，数据元素进队列的过程称为 "入队"，出队列的过程称为 "出队"。

不仅如此，队列中数据的进出要遵循 "先进先出" 的原则，即最先进队列的数据元素，同样要最先出队列。拿图 1 中的队列来说，从数据在队列中的存储状态可以分析出，元素 1 最先进队，其次是元素 2，最后是元素 3。此时如果将元素 3 出队，根据队列 "先进先出" 的特点，元素 1 要先出队列，元素 2 再出队列，最后才轮到元素 3 出队列。

栈和队列不要混淆，栈结构是一端封口，特点是"先进后出"；而队列的两端全是开口，特点是"先进先出"。

因此，数据从表的一端进，从另一端出，且遵循 "先进先出" 原则的线性存储结构就是队列。

队列存储结构的实现有以下两种方式：

1. 顺序队列：在顺序表基础上实现的队列结构；
2. 链队列：在链表的础上实现的队列结构；

两者的区别仅是顺序表和链表的区别，即在实际的物理空间中，数据集中存储的队列是顺序队列，分散存储的队列是链队列。

实际生活中，队列的应用随处可见，比如排队买 XXX、医院的挂号系统等，采用的都是队列的结构。

拿排队买票来说，所有的人排成一队，先到者排的就靠前，后到者只能从队尾排队等待，队中的每个人都必须等到自己前面的所有人全部买票成功并从队头出队后，才轮到自己买票。这就不是典型的队列结构吗？

明白了什么是队列，接下来开始系统地学习顺序队列和链队列。

---

八、顺序队列及C语言实现（2种方案）

顺序队列，即采用顺序表模拟实现的队列结构。

我们知道，队列具有以下两个特点：

1. 数据从队列的一端进，另一端出；
2. 数据的入队和出队遵循"先进先出"的原则；

因此，只要使用顺序表按以上两个要求操作数据，即可实现顺序队列。首先来学习一种最简单的实现方法。

1、顺序队列简单实现

由于顺序队列的底层使用的是数组，因此需预先申请一块足够大的内存空间初始化顺序队列。除此之外，为了满足顺序队列中数据从队尾进，队头出且先进先出的要求，我们还需要定义两个指针（top 和 rear）分别用于指向顺序队列中的队头元素和队尾元素，如图 1 所示：

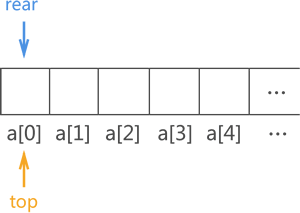
图 1 顺序队列实现示意图

由于顺序队列初始状态没有存储任何元素，因此 top 指针和 rear 指针重合，且由于顺序队列底层实现靠的是数组，因此 top 和 rear 实际上是两个变量，它的值分别是队头元素和队尾元素所在数组位置的下标。

在图 1 的基础上，当有数据元素进队列时，对应的实现操作是将其存储在指针 rear 指向的数组位置，然后 rear+1；当需要队头元素出队时，仅需做 top+1 操作。

例如，在图 1 基础上将?{1,2,3,4}?用顺序队列存储的实现操作如图 2 所示：

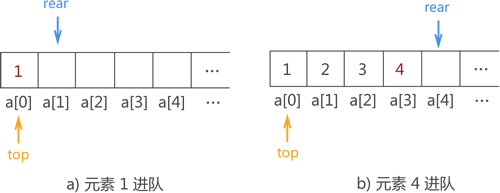
图 2 数据进顺序队列的过程实现示意图

在图 2 基础上，顺序队列中数据出队列的实现过程如图 3 所示：

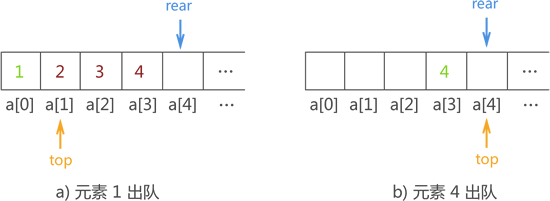
图 3 数据出顺序队列的过程示意图

因此，使用顺序表实现顺序队列最简单方法的 C 语言实现代码为：

#include <stdio.h>

int enQueue(int *a,int rear,int data){

????????a[rear]=data;

????????rear++;

????????return rear;

}

void deQueue(int *a,int front,int rear){

????????//如果 front==rear，表示队列为空

????????while (front!=rear) {

????????????????printf("出队元素：%d\n",a[front]);

????????????????front++;

????????}

}

int main() {

????????int a[100];

????????int front,rear;

????????//设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址

????????front=rear=0;

????????//入队

????????rear=enQueue(a, rear, 1);

????????rear=enQueue(a, rear, 2);

????????rear=enQueue(a, rear, 3);

????????rear=enQueue(a, rear, 4);

????????//出队

????????deQueue(a, front, rear);

????????return 0;

}

程序输出结果：

出队元素：1
出队元素：2
出队元素：3
出队元素：4

（1）此方法存在的问题

先来分析以下图 2b) 和图 3b)。图 2b) 是所有数据进队成功的示意图，而图 3b) 是所有数据全部出队后的示意图。通过对比两张图，你会发现，指针 top 和 rear 重合位置指向了? a[4] 而不再是 a[0]。也就是说，整个顺序队列在数据不断地进队出队过程中，在顺序表中的位置不断后移。

顺序队列整体后移造成的影响是：

• 顺序队列之前的数组存储空间将无法再被使用，造成了空间浪费；
• 如果顺序表申请的空间不足够大，则直接造成程序中数组 a 溢出，产生溢出错误；

为了避免以上两点，我建议初学者使用下面的方法实现顺序队列。

2、顺序队列另一种实现方法

既然明白了上面这种方法的弊端，那么我们可以试着在它的基础上对其改良。

为了解决以上两个问题，可以使用巧妙的方法将顺序表打造成一个环状表，如图 4 所示：

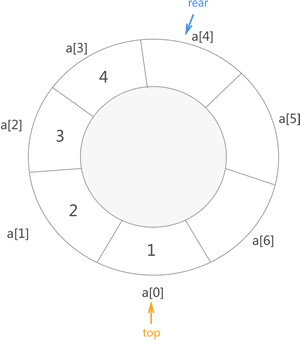
图 4 环状顺序队列

图 4 只是一个想象图，在真正的实现时，没必要真创建这样一种结构，我们还是使用之前的顺序表，也还是使用之前的程序，只需要对其进行一点小小的改变：

#include <stdio.h>

#define max 5//表示顺序表申请的空间大小

int enQueue(int *a,int front,int rear,int data){

????????//添加判断语句，如果rear超过max，则直接将其从a[0]重新开始存储，如果rear+1和front重合，则表示数组已满

????????if ((rear+1)%max==front) {

????????????????printf("空间已满");

????????????????return rear;

????????}

????????a[rear%max]=data;

????????rear++;

????????return rear;

}

int deQueue(int *a,int front,int rear){

????????//如果front==rear，表示队列为空

????????if(front==rear%max) {

????????????????printf("队列为空");

????????????????return front;

????????}

????????printf("%d ",a[front]);

????????//front不再直接 +1，而是+1后同max进行比较，如果=max，则直接跳转到 a[0]

????????front=(front+1)%max;

????????return front;

}

int main() {

????????int a[max];

????????int front,rear;

????????//设置队头指针和队尾指针，当队列中没有元素时，队头和队尾指向同一块地址

????????front=rear=0;

????????//入队

????????rear=enQueue(a,front,rear, 1);

????????rear=enQueue(a,front,rear, 2);

????????rear=enQueue(a,front,rear, 3);

????????rear=enQueue(a,front,rear, 4);

????????//出队

????????front=deQueue(a, front, rear);

????????//再入队

????????rear=enQueue(a,front,rear, 5);

????????//再出队

????????front=deQueue(a, front, rear); /

????????/再入队

????????rear=enQueue(a,front,rear, 6);

????????//再出队

????????front=deQueue(a, front, rear);

????????front=deQueue(a, front, rear);

????????front=deQueue(a, front, rear);

????????front=deQueue(a, front, rear);

????????return 0;

}

程序运行结果：

1 2 3 4 5 6

使用此方法需要注意的是，顺序队列在判断数组是否已满时，出现下面情况：

• 当队列为空时，队列的头指针等于队列的尾指针；
• 当数组满员时，队列的头指针等于队列的尾指针；

顺序队列的存储状态不同，但是判断条件相同。为了对其进行区分，最简单的解决办法是：牺牲掉数组中的一个存储空间，判断数组满员的条件是：尾指针的下一个位置和头指针相遇，就说明数组满了，即程序中第 5 行所示。