数据预处理:多重共线性_检测和解决办法
文章目录
1.多重共线性简介(Collinearity and Multicollinearity)
多重共线性(Collinearity)指的是预测变量,也称为自变量,彼此之间并不是完全独立的。

共线性是指两个特征之间存在线性关系(高度相关),并且它们被用作目标的预测变量。通常使用皮尔逊相关系数来衡量。多于两个预测变量之间也可能存在共线性(并且通常是这种情况)。
多重共线性这个术语最初是由Ragnar Frisch提出的。多重共线性是共线性的一种特殊情况,其中一个特征与两个或更多特征呈线性关系。我们也可能出现这样的情况:多于两个特征之间存在相关性,但同时它们之间没有高度相关性。
在多元回归中,部分多重共线性是普遍存在的。两个随机变量在样本中几乎总是会在某种程度上相关,即使它们在更大的总体中没有任何基本关系。换句话说,多重共线性是一个程度问题。
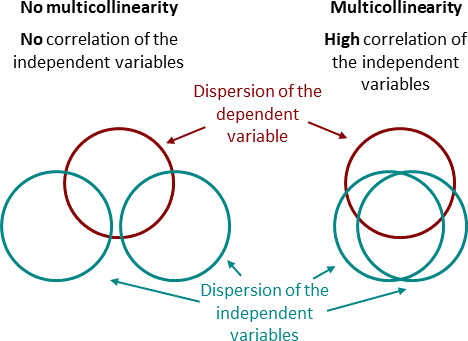
1.1 多重共线性的后果
多重共线性可能在模型拟合过程中导致重大问题。它会降低回归和分类模型的整体性能:
- 不会增加偏差,但可能会增加方差(过拟合);
- 使估计值对模型中的微小变化非常敏感;
- 不会影响预测能力,但可能会错误地计算出各个预测变量对响应变量的影响。
结果是,系数估计值不稳定且难以解释。多重共线性削弱了分析的统计功效,可能导致系数改变符号,并且使得正确指定模型更加困难。
1.2 处理多重共线性问题的方法
-
增加样本量。增加样本量会引入更多的数据序列变化,从而减少抽样误差的影响,并在估计数据的各种属性时提高精确度。增加样本量可以减少多重共线性的存在或影响,或者两者都可以减少。
-
删除一些高度相关的特征。
- 手动方法 - 方差膨胀因子(VIF)
- 自动方法 - 递归特征消除(RFE)
- 使用PCA分解进行特征消除(在本研究中将跳过此方法)
-
用它们的线性组合替换高度相关的回归变量。
-
在特征工程中保持常识 - 理解自己在做什么。
-
使用正则化方法,如岭回归(RIDGE)和套索回归(LASSO)或贝叶斯回归。
2. 设置
2.1 导入库
# 导入必要的库
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.model_selection import cross_val_score
from sklearn import metrics
from collections import Counter
# 在jupyter notebook中显示图形
%matplotlib inline
2.2 数据集特征
波士顿房价
https://www.kaggle.com/datasets/vikrishnan/boston-house-prices
数据库中的每条记录描述了波士顿的一个郊区或城镇。该数据来自于1970年波士顿标准都市统计区(SMSA)。属性定义如下(取自UCI机器学习库1):
- CRIM:城镇人均犯罪率
- ZN:住宅用地超过 25,000 平方英尺的比例
- INDUS:城镇非零售商业用地的比例
- CHAS:查尔斯河虚拟变量(如果 Tract 限制河流,则为1;否则为0)
- NOX:一氧化氮浓度(每千万份)
- RM:每个住宅的平均房间数
- AGE:1940年之前建成的自用房屋比例
- DIS:到五个波士顿就业中心的加权距离
- RAD:径向公路的可达性指数
- TAX:每 10,000 美元的全额物业税率
- PTRATIO:城镇师生比例
- B:1000(Bk-0.63)^2,其中Bk是城镇黑人的比例
- LSTAT:人口中地位较低者的百分比
- MEDV:自住房屋房价中位数(以千美元为单位)
缺失属性值:无
这是UCI ML房屋数据集的副本。
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
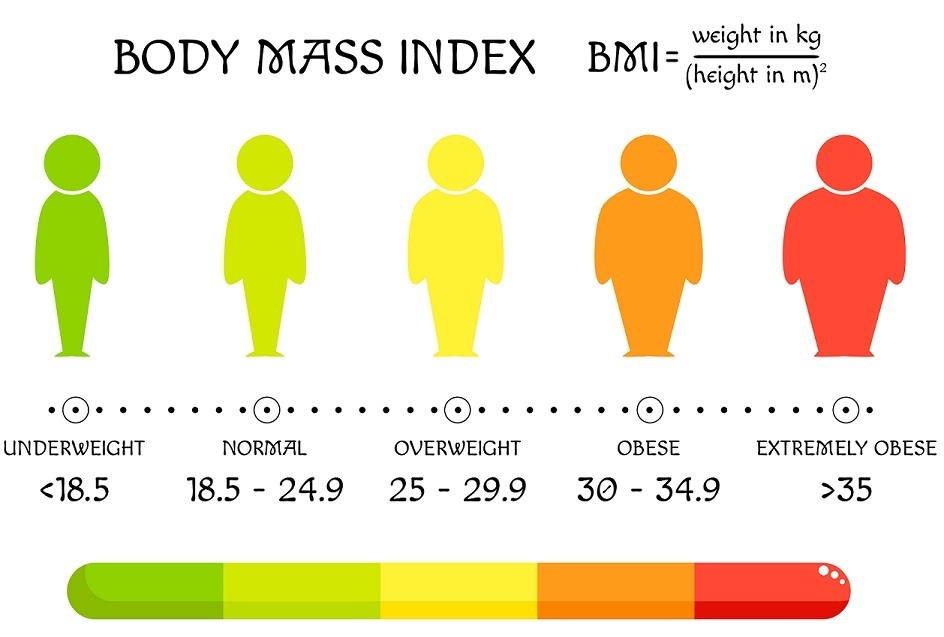
BMI 数据集
https://www.kaggle.com/datasets/yasserh/bmidataset
此数据框包含以下列:
性别:男/女
身高:数字(厘米)
体重:数字(千克)
指数:
0 - 极度虚弱
1 - 虚弱
2 - 正常
3 - 超重
4 - 肥胖
5 - 极度肥胖
2.3 导入数据
# 定义列名
column_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
# 读取波士顿房价数据集
raw_boston = pd.read_csv('../input/boston-house-prices/housing.csv', header=None, delimiter=r"\s+", names=column_names)
# 读取BMI数据集
raw_bmi = pd.read_csv('../input/bmidataset/bmi.csv')
# 创建一个名为"Gender"的新列,用于存储性别的虚拟变量
# 将"Gender"列中的"Male"替换为0,"Female"替换为1,以创建性别的虚拟变量
raw_bmi['Gender'] = raw_bmi['Gender'].map({'Male':0, 'Female':1})
3. 相关矩阵
相关矩阵给出了两个独立变量之间的成对相关性或双变量关系 - 共线性。它是一个显示不同变量之间相关系数的表格。它接受具有数值列的输入关系,并计算其输入列之间的皮尔逊相关系数。
该矩阵显示了表格中所有可能值对之间的相关性。它是总结大型数据集并识别和可视化给定数据中的模式的强大工具。如果相关矩阵显示出具有高绝对值的元素,我们可以谈论共线性。在极端情况下,解释变量完全重叠。
### 绘制各列之间的相关性热力图
plt.figure(figsize = (6, 6)) # 创建一个6x6的图像窗口
heatmap = sns.heatmap(raw_bmi.corr(), vmin = -1, vmax = 1, annot = True) # 使用sns.heatmap函数绘制热力图,传入数据为raw_bmi的相关性矩阵,vmin和vmax参数指定颜色映射的范围为-1到1,annot参数为True表示在热力图上显示相关系数的数值
heatmap.set_title('BMI Correlation Heatmap', fontdict = {'fontsize' : 18}, pad = 12) # 设置热力图的标题为'BMI Correlation Heatmap',字体大小为18,标题与图像之间的间距为12像素
Text(0.5, 1.0, 'BMI Correlation Heatmap')

我们可以看到“指数”和“身高”/“体重”之间存在很强的相关性(如预期所示)。
我们还可以注意到,“体重”对“指数”的影响要比“身高”大得多。这也是直观和预期的。
### 绘制各列之间的相关性热力图
plt.figure(figsize = (13, 13)) # 创建一个大小为13x13的图像画布
heatmap = sns.heatmap(raw_boston.corr(), vmin = -1, vmax = 1, annot = True) # 使用seaborn库的heatmap函数绘制热力图,传入数据为raw_boston的相关性矩阵,设置颜色映射范围为-1到1,同时在图中显示相关系数的数值
heatmap.set_title('Boston Correlation Heatmap', fontdict = {'fontsize' : 18}, pad = 12) # 设置热力图的标题为'Boston Correlation Heatmap',设置标题的字体大小为18,设置标题与图像之间的距离为12像素
Text(0.5, 1.0, 'Boston Correlation Heatmap')

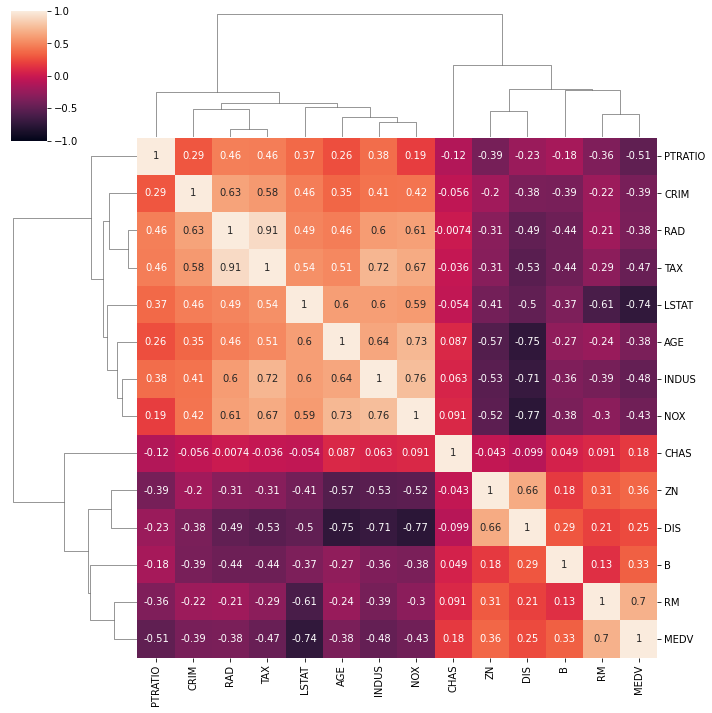
3.1 聚类图
聚类图表不仅显示了变量之间的所有相关性,还显示了它们之间的分组(聚类)关系。
# 设置绘图大小
plt.figure(figsize = (4, 4))
# 使用Seaborn库的clustermap函数绘制聚类热力图
# raw_boston.corr()计算Boston房价数据集中各变量之间的相关系数矩阵
# vmin和vmax分别设置热力图颜色条的最小值和最大值
# annot=True表示在热力图上显示相关系数数值
clustermap = sns.clustermap(raw_boston.corr(), vmin = -1, vmax = 1, annot = True)
<Figure size 288x288 with 0 Axes>
4. 方差膨胀因子
方差膨胀因子(VIF)是回归分析中多重共线性程度的衡量指标。VIF用于确定一个自变量与一组其他变量之间的相关性。
V I F i = 1 1 ? R i 2 VIF_i = \frac {1}{1-R_i^2} VIFi?=1?Ri2?1?
在回归分析中,当两个或更多的变量之间存在线性关系时,存在多重共线性。VIF通过衡量给定回归变量与其他回归变量的线性相关性,增加了其系数估计的方差,相对于没有相关性的基准情况。
VIF告诉我们预测变量之间的相关性如何膨胀方差。例如,VIF为10表示现有的多重共线性使系数的方差相对于没有多重共线性模型增加了10倍。
VIF没有任何上限。数值越低越好。大于4或5的值有时被认为是中度到高度的,而大于10的值被认为是非常高的。
因此,通常将VIF = 5作为阈值。这意味着任何大于5的自变量都必须被移除。尽管理想的阈值值取决于具体情况,在许多计量经济学教科书中,只有当VIF > 10时才被认为是严重的多重共线性。
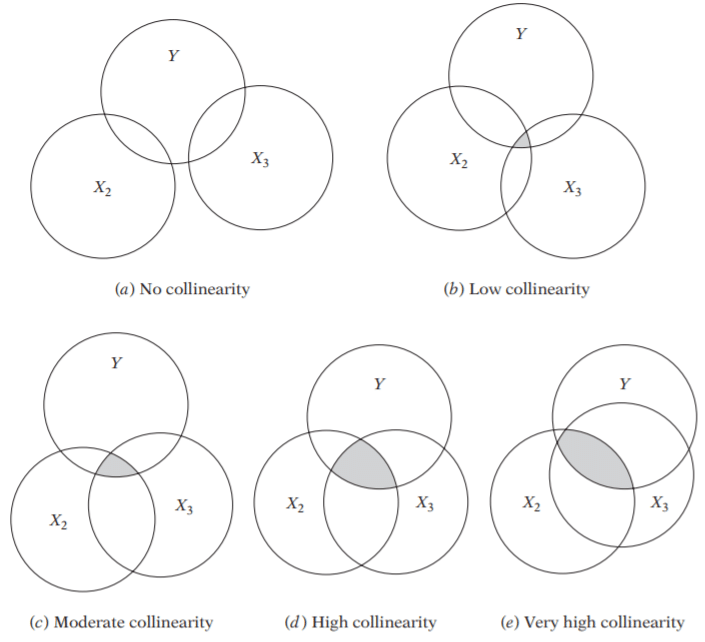
4.1 两种多重共线性
- 基于数据的多重共线性:这种类型的多重共线性存在于数据本身中。观察性实验更有可能展现这种类型的多重共线性。
- 例如:两个相同(或几乎相同)的变量。磅重和公斤重,或者投资收入和储蓄/债券收入。
- 结构性多重共线性:由研究人员创建新的预测变量引起。当我们使用其他术语创建模型术语时,就会出现这种类型。换句话说,它是我们指定的模型的副产品。
- 在回归中包括一个实际上是两个其他变量的组合的变量。例如,在回归中包括“总投资收入”,而总投资收入=股票和债券收入+储蓄利息收入。
4.2 基于数据的多重共线性
让我们使用3个特征:‘性别’、‘身高’和’体重’,来检查一个BMI数据库的VIF。
# 导入必要的库已经完成,不再赘述
# 定义自变量集合
X = raw_bmi[['Gender', 'Height', 'Weight']]
# 创建一个空的VIF数据框
vif_data = pd.DataFrame()
# 将自变量的名称添加到VIF数据框中
vif_data["Feature"] = X.columns
# 计算每个自变量的VIF值
vif_data["VIF"] = [variance_inflation_factor(X.values, i)
for i in range(len(X.columns))]
# 打印VIF数据框
print(vif_data)
Feature VIF
0 Gender 2.028864
1 Height 11.623103
2 Weight 10.688377
‘Height’ 和 ‘Weight’ 的VIF值很高,表明这两个变量高度相关。这是可以预期的,因为一个人的身高确实会影响他们的体重。因此,考虑这两个特征仍然会导致一个具有高多重共线性的模型。
4.3 结构性多重共线性
现在让我们使用4个特征:‘Gender’、‘Height’、‘Weight’和’Index’,来检查BMI数据库的VIF。
# 定义语料
# 独立变量集
X = raw_bmi[['Gender', 'Height', 'Weight', 'Index']]
# 创建一个空的VIF数据框
vif_data = pd.DataFrame()
# 在VIF数据框中添加特征列
vif_data["Feature"] = X.columns
# 计算每个特征的VIF
vif_data["VIF"] = [variance_inflation_factor(X.values, i)
for i in range(len(X.columns))]
# 打印VIF数据框
print(vif_data)
Feature VIF
0 Gender 2.031010
1 Height 11.941301
2 Weight 40.024880
3 Index 25.143752
有一个显著的差异!'Weight’的VIF值大于40,'Index’的VIF值大于25!
我知道在数据集中有’Index’,但请思考一下’Index’实际代表什么。我们可以将其视为其他特征的派生特征。在特征工程中创建这样的新特征非常常见。
无论如何,我们可以将其视为研究人员创造的多重共线性的一个很好的例子。
5. 基于VIF的特征降维
让我们使用VIF检查波士顿数据框中的多重共线性。
# 导入所需的库
# 从raw_boston数据集中选择独立变量集合,存储在X2中
X2 = raw_boston[['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']]
# 创建一个空的DataFrame,用于存储VIF值
vif2_data = pd.DataFrame()
# 在vif2_data中创建一个名为"Feature"的列,用于存储特征名称
vif2_data["Feature"] = X2.columns
# 计算每个特征的VIF值,并将结果存储在vif2_data的"VIF"列中
vif2_data["VIF"] = [variance_inflation_factor(X2.values, i)
for i in range(len(X2.columns))]
# 打印vif2_data,显示每个特征的VIF值
print(vif2_data)
Feature VIF
0 CRIM 2.100373
1 ZN 2.844013
2 INDUS 14.485758
3 CHAS 1.152952
4 NOX 73.894947
5 RM 77.948283
6 AGE 21.386850
7 DIS 14.699652
8 RAD 15.167725
9 TAX 61.227274
10 PTRATIO 85.029547
11 B 20.104943
12 LSTAT 11.102025
我们这里有一些很大的VIF值!让我们在接下来的步骤中删除一些高度相关的特征。
重要提示:我们应该逐步进行,一次删除一个特征并检查结果。
# 定义自变量集合
X2 = raw_boston[['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'B', 'LSTAT']]
# 创建一个空的DataFrame用于存储VIF值
vif2_data = pd.DataFrame()
# 将特征列添加到DataFrame中
vif2_data["Feature"] = X2.columns
# 计算每个特征的VIF值
vif2_data["VIF"] = [variance_inflation_factor(X2.values, i)
for i in range(len(X2.columns))]
# 打印VIF值的DataFrame
print(vif2_data)
Feature VIF
0 CRIM 2.099345
1 ZN 2.451624
2 INDUS 14.275283
3 CHAS 1.142167
4 NOX 73.894171
5 RM 60.598846
6 AGE 21.361234
7 DIS 12.221605
8 RAD 15.159162
9 TAX 59.301541
10 B 18.614751
11 LSTAT 10.138324
在仅删除PTRATIO之后,VIF值发生了显著变化!但是其他特征仍然具有较高的VIF值。
让我们进一步删除更多的特征,直到所有特征的VIF值都低于10。
我不会在这里展示所有的步骤 - 你可以自己查看。
最后一步需要7个特征。
# 定义自变量集合
X2 = raw_boston[['CRIM', 'ZN', 'INDUS', 'CHAS', 'DIS', 'RAD', 'LSTAT']]
# 创建一个空的DataFrame用于存储VIF值
vif2_data = pd.DataFrame()
# 将自变量的名称存储在DataFrame的"Feature"列中
vif2_data["Feature"] = X2.columns
# 计算每个自变量的VIF值
vif2_data["VIF"] = [variance_inflation_factor(X2.values, i)
for i in range(len(X2.columns))]
# 打印VIF值的DataFrame
print(vif2_data)
Feature VIF
0 CRIM 2.067135
1 ZN 2.299351
2 INDUS 6.900077
3 CHAS 1.086574
4 DIS 3.968908
5 RAD 4.678181
6 LSTAT 6.726973
现在我们已经拥有所有VIF值小于10的特征。
在接下来的步骤中,我们将比较包含所有特征的线性回归模型与使用VIF删除特征后的模型。
6. 回归模型性能比较
6.1 数据预处理
# 将原始波士顿数据集复制到新的变量scaled_boston中,以便进行缩放处理。
scaled_boston = raw_boston.copy()
# 导入StandardScaler类
from sklearn.preprocessing import StandardScaler
# 定义特征列名
col_names = ['CRIM', 'ZN', 'INDUS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
# 从scaled_boston中提取特征数据
features = scaled_boston[col_names]
# 创建StandardScaler对象,并使用特征数据进行拟合
scaler = StandardScaler().fit(features.values)
# 使用拟合后的scaler对特征数据进行标准化处理
features = scaler.transform(features.values)
# 将标准化后的特征数据更新到scaled_boston中
scaled_boston[col_names] = features
# 提取特征变量X和目标变量y
X = scaled_boston.iloc[:, :-1].values
y = scaled_boston.iloc[:, -1].values
# X是特征变量,包含所有行和除最后一列之外的所有列
# y是目标变量,包含所有行和最后一列的值
6.2 回归评估指标
平均绝对误差(MAE)是误差绝对值的平均值:
1 n ∑ i = 1 n ∣ y i ? y ^ i ∣ \frac 1n\sum_{i=1}^n|y_i-\hat{y}_i| n1?i=1∑n?∣yi??y^?i?∣
均方误差(MSE)是误差平方的平均值:
1 n ∑ i = 1 n ( y i ? y ^ i ) 2 \frac 1n\sum_{i=1}^n(y_i-\hat{y}_i)^2 n1?i=1∑n?(yi??y^?i?)2
均方根误差(RMSE)是均方误差的平方根:
1 n ∑ i = 1 n ( y i ? y ^ i ) 2 \sqrt{\frac 1n\sum_{i=1}^n(y_i-\hat{y}_i)^2} n1?i=1∑n?(yi??y^?i?)2?
对比这些指标:
-
MAE 是平均误差。平均绝对误差表示数据集中实际值和预测值之间绝对差异的平均值。它衡量数据集中残差的平均值。
-
MSE 由于MSE“惩罚”较大的误差,在现实世界中往往很有用。均方误差表示数据集中原始值和预测值之间平方差的平均值。它衡量残差的方差。
-
RMSE 在“y”单位中是可解释的。均方根误差是均方误差的平方根。它衡量残差的标准差。
所有这些都是损失函数,因为我们希望将它们最小化。
- R平方 决定系数或R平方表示因变量方差中由线性回归模型解释的比例。当R2较高时,表示回归可以捕捉观察到的因变量的大部分变异。因此,当R2较高时,我们可以说回归模型的性能较好。
它是一个无量纲的分数,即不考虑值的大小,R平方的值将小于一。关于回归分析的一个误解是,低R平方值总是不好的。例如,某些数据集或研究领域本质上具有更多的未解释变异。在这种情况下,R平方值自然会较低。即使R平方值较低,研究人员仍然可以对数据做出有用的结论。
R a d j . 2 = 1 ? ( 1 ? R 2 ) ? n ? 1 n ? p ? 1 R^2_{adj.} = 1 - (1-R^2)*\frac{n-1}{n-p-1} Radj.2?=1?(1?R2)?n?p?1n?1?
- 调整R平方 是R平方的修改版本,它根据模型中的独立变量数量进行了调整,并且始终小于或等于R2。在下面的公式中,n是数据中的观测数,k是数据中的独立变量数。
结论
RMSE和R平方都量化了线性回归模型拟合数据集的程度。在评估模型拟合数据集的程度时,计算RMSE和R2值是有用的,因为每个指标都告诉我们不同的信息。
-
RMSE告诉我们回归模型预测值与实际值之间的典型距离。
-
R2告诉我们预测变量能够解释响应变量的变异程度。
向回归模型添加更多的独立变量或预测变量往往会增加R2值,这会引诱模型制作者添加更多的变量。调整R2用于确定相关性的可靠性以及它受独立变量添加的影响程度。它始终低于R2。
我们将使用的最后一个指标是交叉验证的R2。
交叉验证是一种用于评估机器学习模型的重采样过程,用于有限的数据样本。
交叉验证是一种流行的方法,因为它简单易懂,并且通常会得出比其他方法(如简单的训练/测试拆分)更少偏差或乐观估计的模型技能。
7. 线性回归
# 使用train_test_split函数将数据集划分为训练集和测试集
# 参数X表示特征数据集,y表示目标数据集
# 参数test_size表示测试集所占比例,这里设置为0.3,即测试集占总数据集的30%
# 参数random_state表示随机种子,这里设置为42,保证每次划分的结果一致
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 42)
# 导入LinearRegression线性回归模型
# 创建并训练模型
lm = LinearRegression() # 创建一个线性回归模型对象
lm.fit(X_train, y_train) # 使用训练数据对模型进行训练
# 模型对测试数据进行预测
y_pred = lm.predict(X_test) # 使用训练好的模型对测试数据进行预测,得到预测结果y_pred
# 预测交叉验证分数
cv_lm = cross_val_score(estimator=lm, X=X_train, y=y_train, cv=10)
# 计算调整后的R-squared
r2 = lm.score(X_test, y_test)
# 观测值的数量是沿着轴0的形状
n = X_test.shape[0]
# 特征的数量(预测变量,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R-squared公式
lm_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
lm_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
lm_R2 = lm.score(X_test, y_test)
lmCV_R2 = cv_lm.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 4))
print('R2:', round(lm.score(X_test, y_test), 4))
print('Adjusted R2:', round(lm_adjusted_r2, 4))
print("Cross Validated R2: ", round(cv_lm.mean(), 4))
RMSE: 4.6387
R2: 0.7112
Adjusted R2: 0.684
Cross Validated R2: 0.6875
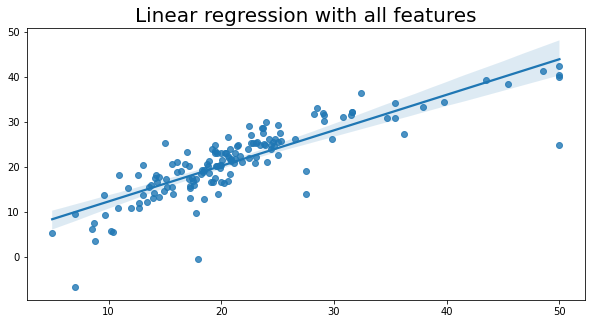
# 设置图形的大小
plt.figure(figsize=(10, 5))
# 绘制回归图
sns.regplot(x=y_test, y=y_pred)
# 设置图形的标题和字体大小
plt.title('Linear regression with all features', fontsize=20)
Text(0.5, 1.0, 'Linear regression with all features')
8. 随机森林
# 导入RandomForestRegressor类
from sklearn.ensemble import RandomForestRegressor
# 创建和训练模型
RandomForest_reg = RandomForestRegressor(n_estimators = 10, random_state = 0) # 创建一个随机森林回归模型,包含10个决策树,随机种子为0
RandomForest_reg.fit(X_train, y_train) # 使用训练数据集X_train和y_train来训练模型
# 模型对测试数据进行预测
y_pred = RandomForest_reg.predict(X_test) # 使用训练好的模型对测试数据集X_test进行预测,预测结果存储在y_pred中
# 预测交叉验证分数
cv_rf = cross_val_score(estimator=RandomForest_reg, X=X_train, y=y_train, cv=10)
# 计算调整后的R平方
r2 = RandomForest_reg.score(X_test, y_test)
# 观测值的数量是沿着轴0的形状
n = X_test.shape[0]
# 特征的数量(预测变量,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R平方公式
rf_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
rf_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
rf_R2 = RandomForest_reg.score(X_test, y_test)
rfCV_R2 = cv_rf.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 4))
print('R2:', round(RandomForest_reg.score(X_test, y_test), 4))
print('Adjusted R2:', round(rf_adjusted_r2, 4))
print("Cross Validated R2: ", round(cv_rf.mean(), 4))
RMSE: 3.3291
R2: 0.8513
Adjusted R2: 0.8373
Cross Validated R2: 0.8171
结果
随机森林模型的结果看起来好多了!
9. 使用VIF删除特征后的线性回归
# 复制scaled_boston数据集并将其命名为scaled_boston2
scaled_boston2 = scaled_boston.copy()
# 从scaled_boston2数据集中删除'NOX', 'RM', 'AGE', 'TAX', 'PTRATIO', 'B'这些列
scaled_boston2 = scaled_boston2.drop(['NOX', 'RM', 'AGE', 'TAX', 'PTRATIO', 'B'], axis=1)
# 提取特征变量X
X = scaled_boston2.iloc[:, :-1].values
# 提取目标变量y
y = scaled_boston2.iloc[:, -1].values
# 使用train_test_split函数将数据集分割为训练集和测试集
# 参数X为特征数据,y为目标数据
# test_size表示测试集占总数据集的比例,这里设置为0.3,即测试集占总数据集的30%
# random_state用于设置随机种子,保证每次运行代码得到的结果一致
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 42)
# 创建一个线性回归模型对象
lm2 = LinearRegression()
# 使用训练数据来训练线性回归模型
lm2.fit(X_train, y_train)
# 使用训练好的模型对测试数据进行预测
y_pred = lm2.predict(X_test)
# 设置图形的大小为10x5
plt.figure(figsize=(10, 5))
# 绘制回归图,x轴为y_test,y轴为y_pred
sns.regplot(x=y_test, y=y_pred)
# 设置图形的标题为'Linear regression after dropping features',字体大小为20
plt.title('Linear regression after dropping features', fontsize=20)
Text(0.5, 1.0, 'Linear regression after dropping features')

# 预测交叉验证分数
cv_lm2 = cross_val_score(estimator=lm2, X=X_train, y=y_train, cv=10)
# 计算调整后的R平方
r2 = lm2.score(X_test, y_test)
# 观测值的数量是沿着轴0的形状
n = X_test.shape[0]
# 特征的数量(预测变量,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R平方公式
lm2_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
lm2_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
lm2_R2 = lm2.score(X_test, y_test)
lm2CV_R2 = cv_lm2.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 4))
print('R2:', round(lm2.score(X_test, y_test), 4))
print('Adjusted R2:', round(lm2_adjusted_r2, 4))
print("Cross Validated R2: ", round(cv_lm2.mean(), 4))
RMSE: 5.4573
R2: 0.6003
Adjusted R2: 0.5809
Cross Validated R2: 0.606
如我们所见 - 结果看起来并不好!
我们稍后会讨论这个问题。
10. 使用VIF方法删除特征后的随机森林模型
# 创建和训练模型
RandomForest2_reg = RandomForestRegressor(n_estimators = 10, random_state = 0)
# 使用随机森林回归器模型,设置10个决策树,随机种子为0
RandomForest2_reg.fit(X_train, y_train)
# 使用训练好的模型对测试数据进行预测
y_pred = RandomForest2_reg.predict(X_test)
# 预测交叉验证分数
cv_rf2 = cross_val_score(estimator=RandomForest2_reg, X=X_train, y=y_train, cv=10)
# 计算调整后的R平方
r2 = RandomForest2_reg.score(X_test, y_test)
# 观测值数量是沿着轴0的形状
n = X_test.shape[0]
# 特征数量(预测变量,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R平方公式
rf2_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
rf2_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
rf2_R2 = RandomForest2_reg.score(X_test, y_test)
rf2CV_R2 = cv_rf2.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 4))
print('R2:', round(RandomForest2_reg.score(X_test, y_test), 4))
print('Adjusted R2:', round(rf2_adjusted_r2, 4))
print("Cross Validated R2: ", round(cv_rf2.mean(), 4))
RMSE: 4.4068
R2: 0.7394
Adjusted R2: 0.7267
Cross Validated R2: 0.7554
再一次。在删除特征之后,我们的结果比之前更差。
11. 递归特征消除(RFE)
递归特征消除(RFE)是一种通过递归地考虑特征子集来选择特征的方法。它通过反复构建模型并选择最佳或最差的特征(根据模型的性能)来实现。在每次迭代中,它会将最佳或最差的特征从特征集中移除,然后继续迭代,直到达到预设的特征数量。
RFE的主要思想是通过递归地消除特征,来选择最佳的特征子集。它可以用于特征选择和特征排名。在每次迭代中,它会根据模型的性能选择最佳或最差的特征,并将其从特征集中移除。然后,它会继续迭代,直到达到预设的特征数量。
RFE的步骤如下:
- 选择一个机器学习模型作为基础模型。
- 根据模型的性能选择最佳或最差的特征。
- 将选择的特征从特征集中移除。
- 重复步骤2和3,直到达到预设的特征数量。
RFE的优点包括:
- 可以自动选择特征子集,无需手动选择。
- 可以通过递归地消除特征来选择最佳的特征子集。
然而,RFE也有一些限制:
- 如果特征之间存在高度相关性,RFE可能会选择其中一个特征,而忽略其他相关特征。
- RFE的计算成本较高,特别是在特征数量较多的情况下。
总之,递归特征消除(RFE)是一种通过递归地考虑特征子集来选择特征的方法。它可以用于特征选择和特征排名,但也有一些限制。
递归特征消除(RFE)是一种向后特征选择算法。
该算法通过多次拟合模型并在每一步中根据拟合模型的coef_或feature_importances_属性删除最弱的特征,从而从模型中消除n个特征。
RFE通过从训练数据集中的所有特征开始,成功删除特征直到剩下所需数量的特征来搜索特征子集。
RFE是一种包装型特征选择算法。这意味着在方法的核心中给定并使用了不同的机器学习算法,由RFE包装,并用于帮助选择特征。
并非所有模型都可以与RFE方法配对,有些模型比其他模型更受益于RFE。因为RFE要求初始模型使用完整的预测变量集,所以当预测变量的数量超过样本数量时,某些模型无法使用。这些模型包括多元线性回归、逻辑回归和线性判别分析。如果我们希望将其中一种技术与RFE一起使用,则必须首先缩小预测变量的范围。此外,某些模型比其他模型更受益于使用RFE。随机森林就是这样一个模型(Svetnik等人,2003)。
向后选择经常与随机森林模型一起使用,原因有两个:
- 随机森林倾向于不排除预测方程中的变量;
- 它有一种内部方法来衡量特征重要性。
# 提取特征变量X和目标变量y
X = scaled_boston.iloc[:, :-1].values
y = scaled_boston.iloc[:, -1].values
# X为特征变量,去除最后一列
# y为目标变量,只包含最后一列的值
# 使用train_test_split函数将数据集分为训练集和测试集
# 参数X为特征数据,y为目标数据
# test_size表示测试集所占的比例,这里设置为0.3,即测试集占总数据集的30%
# random_state表示随机种子,这里设置为42,保证每次运行代码得到的结果一致
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 42)
# 导入所需的库
from sklearn.feature_selection import RFE
from sklearn.pipeline import Pipeline
# 创建一个Pipeline对象
# 使用RFE进行特征选择,选择8个特征
rfe = RFE(estimator=RandomForestRegressor(), n_features_to_select=8)
# 创建一个随机森林回归模型
model = RandomForestRegressor()
# 创建一个Pipeline对象,将特征选择和回归模型组合在一起
rf_pipeline = Pipeline(steps=[('s',rfe),('m',model)])
# 使用训练数据进行模型训练
rf_pipeline.fit(X_train, y_train)
# 使用训练好的模型对测试数据进行预测
y_pred = rf_pipeline.predict(X_test)
# 预测交叉验证分数
cv_rf_pipeline = cross_val_score(estimator=rf_pipeline, X=X_train, y=y_train, cv=10)
# 计算调整后的R平方
r2 = rf_pipeline.score(X_test, y_test)
# 观测值的数量是沿着轴0的形状
n = X_test.shape[0]
# 特征的数量(预测变量,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R平方公式
rf_pipeline_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
rf_pipeline_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
rf_pipeline_R2 = rf_pipeline.score(X_test, y_test)
rf_pipelineCV_R2 = cv_rf_pipeline.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 4))
print('R2:', round(rf_pipeline.score(X_test, y_test), 4))
print('Adjusted R2:', round(rf_pipeline_adjusted_r2, 4))
print("Cross Validated R2: ", round(cv_rf_pipeline.mean(), 4))
RMSE: 3.3243
R2: 0.8517
Adjusted R2: 0.8377
Cross Validated R2: 0.8162
看起来使用RFE的随机森林模型更好!
12. 正则化线性模型
12.1 正则化
正则化是一种用于减少模型过拟合的技术。当模型过拟合时,它在训练数据上表现得很好,但在新数据上的表现却很差。正则化通过在损失函数中添加一个正则项来惩罚模型的复杂度,从而减少过拟合的风险。
常见的正则化方法有L1正则化和L2正则化。L1正则化通过在损失函数中添加模型参数的绝对值之和来惩罚模型的复杂度。L2正则化则通过在损失函数中添加模型参数的平方和来惩罚模型的复杂度。这两种方法都可以有效地减少模型的复杂度,从而降低过拟合的风险。
在实际应用中,我们可以通过调整正则化参数来控制正则化的强度。较大的正则化参数会导致模型更加简单,但可能会增加欠拟合的风险。较小的正则化参数则会使模型更加复杂,但可能会增加过拟合的风险。因此,选择合适的正则化参数非常重要。
正则化是机器学习中常用的技术之一,它可以帮助我们构建更加稳健和泛化能力强的模型。在实际应用中,我们经常需要使用正则化来提高模型的性能和鲁棒性。
模型训练中的两个主要问题
在训练模型时,可能会遇到两个主要问题:过拟合和欠拟合。
- 过拟合:当模型在训练集上表现良好,但在测试数据上表现不佳时。
- 欠拟合:当模型在训练集和测试集上都表现不佳时。
特别是在训练集和测试集性能之间存在较大差异时,会实施正则化以避免数据过拟合。通过正则化,训练中使用的特征数量保持不变,但是方程1.1中的系数(w)的大小会减小。
12.2 岭回归
岭回归是线性回归的扩展,它在训练期间向损失函数添加正则化L2惩罚。当存在多个高度相关的变量时,可以使用岭回归。它通过对变量的系数进行惩罚来防止过拟合。岭回归通过向误差函数添加惩罚项来缩小系数的大小,从而减少过拟合。
岭回归的优点:
- 比最小二乘/线性回归更具有抗共线性的鲁棒性;
- 比线性回归对异常值不那么敏感(但仍然敏感);
- 不需要数据完全归一化;
- 即使变量的数量大于观测值的数量,也可以应用。
岭回归的缺点:
- 可能需要更多的数据才能获得准确的结果;
- 可能需要更多的计算资源;
- 结果可能难以解释,因为岭项或L2范数修改了系数;
- 如果数据包含异常值,则对异常值敏感,可能产生不稳定的结果。
# 提取特征和目标变量
X = scaled_boston.iloc[:, :-1].values # 提取所有行的除最后一列外的所有列作为特征
y = scaled_boston.iloc[:, -1].values # 提取所有行的最后一列作为目标变量
# 将数据集X和标签y按照30%的比例分割成训练集和测试集
# random_state = 42表示随机种子为42,保证每次运行程序分割的数据集一致
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 42)
# 导入Ridge模型类
from sklearn.linear_model import Ridge
# 创建并训练模型
ridge_reg = Ridge(alpha=1, solver="cholesky") # 创建一个Ridge回归模型,设置alpha为1,使用cholesky求解器
ridge_reg.fit(X_train, y_train) # 使用训练数据X_train和对应的目标值y_train来训练模型
# 模型对测试数据进行预测
y_pred = ridge_reg.predict(X_test) # 使用训练好的模型对测试数据X_test进行预测,得到预测结果y_pred
# 预测交叉验证分数
cv_ridge = cross_val_score(estimator=ridge_reg, X=X_train, y=y_train, cv=10)
# 计算调整后的R平方
r2 = ridge_reg.score(X_test, y_test)
# 观测值的数量是沿着轴0的形状
n = X_test.shape[0]
# 特征的数量(预测变量,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R平方公式
ridge_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
ridge_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
ridge_R2 = ridge_reg.score(X_test, y_test)
ridgeCV_R2 = cv_ridge.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 4))
print('R2:', round(ridge_reg.score(X_test, y_test), 4))
print('Adjusted R2:', round(ridge_adjusted_r2, 4))
print("Cross Validated R2: ", round(cv_ridge.mean(), 4))
RMSE: 4.6403
R2: 0.711
Adjusted R2: 0.6838
Cross Validated R2: 0.6882
# 设置图形的大小
plt.figure(figsize=(10, 5))
# 绘制回归图
sns.regplot(x=y_test, y=y_pred)
# 设置图形的标题和字体大小
plt.title('Ridge Regression model', fontsize=20)
Text(0.5, 1.0, 'Ridge Regression model')

12.3 Lasso回归
Lasso回归是一种常见的正则化线性回归方法,其中包含L1惩罚项。Lasso是Least Absolute Shrinkage and Selection Operator的缩写。这种方法的效果是缩小那些对预测任务没有太大贡献的输入变量的系数。
L1惩罚最小化了所有系数的大小,并允许任何系数变为零,从而有效地将输入特征从模型中移除。
LASSO不是一种回归类型,而是一种可以应用于许多回归类型的模型构建和变量选择方法,包括普通最小二乘法、逻辑回归等等。
LASSO的优点:
- 自动特征选择
- 减少过拟合
幸运的是,由于LASSO内置的变量选择功能,它可以处理一些多重共线性问题,而不会损失可解释性。然而,如果共线性过高,LASSO的变量选择性能将开始下降。在这种情况下,Ridge回归更适合。
LASSO的缺点:
- LASSO模型产生的系数是有偏的。添加到模型中的L1惩罚人为地将系数缩小到接近零,或者在某些情况下,完全变为零。这意味着LASSO模型的系数并不代表特征与结果之间真实关系的大小,而是其缩小版本。
- 难以估计标准误差。由于LASSO模型中的系数估计是有偏的,很难对它们进行准确的标准误差估计。这使得难以对它们进行统计检验和建立置信区间等操作。
- 在相关特征方面存在困难。通常情况下,一个特征会被相对任意地选择,而与该特征高度相关的所有其他特征将被有效地从模型中删除。这可能导致错误地得出只有被选择保留在模型中的特征是重要的结论,而实际上其他一些特征可能同样重要甚至更重要。
- 估计不稳定。LASSO模型产生的估计值被认为相对不稳定,这意味着当在稍微不同的数据集上进行训练时,它们可能会发生很大变化。
- 引入超参数。
# 导入Lasso模型类
from sklearn.linear_model import Lasso
# 创建并训练模型
lasso_reg = Lasso(alpha=0.2) # 创建一个Lasso回归模型对象,设置alpha参数为0.2
lasso_reg.fit(X_train, y_train) # 使用训练数据X_train和y_train来训练模型
# 模型对测试数据进行预测
y_pred = lasso_reg.predict(X_test) # 使用训练好的模型对测试数据X_test进行预测,得到预测结果y_pred
# 预测交叉验证分数
cv_lasso = cross_val_score(estimator=lasso_reg, X=X_train, y=y_train, cv=10)
# 计算调整后的R平方
r2 = lasso_reg.score(X_test, y_test)
# 观测值的数量是沿着轴0的形状
n = X_test.shape[0]
# 特征的数量(预测变量,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R平方公式
lasso_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
lasso_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
lasso_R2 = lasso_reg.score(X_test, y_test)
lassoCV_R2 = cv_lasso.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 4))
print('R2:', round(lasso_reg.score(X_test, y_test), 4))
print('Adjusted R2:', round(lasso_adjusted_r2, 4))
print("Cross Validated R2:", round(cv_lasso.mean(), 4))
RMSE: 4.877
R2: 0.6808
Adjusted R2: 0.6507
Cross Validated R2: 0.674
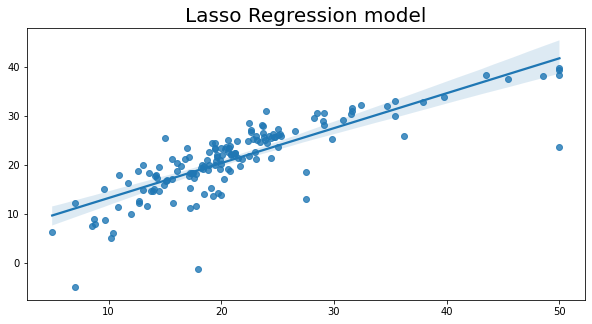
# 设置图形的大小
plt.figure(figsize=(10, 5))
# 绘制回归图
sns.regplot(x=y_test, y=y_pred)
# 设置图形的标题和字体大小
plt.title('Lasso回归模型', fontsize=20)
Text(0.5, 1.0, 'Lasso Regression model')
12.4 贝叶斯岭回归
贝叶斯回归是一种定义和估计统计模型的方法。它可以与任何回归技术一起使用,如线性回归、套索回归等。贝叶斯回归通过使用概率分布而不是点估计来制定线性回归,从而允许自然机制来处理数据不足或分布不良的数据。输出或响应变量’y’被假设为来自概率分布而不是估计为单个值。
当数据集中数据不足或数据分布不良时,贝叶斯回归非常有用。
贝叶斯回归的优点:
- 当数据集的大小较小时非常有效。
- 适用于基于在线学习的场景(实时接收数据),与基于批处理学习相比,在开始训练模型之前,我们手头上有整个数据集。这是因为贝叶斯回归不需要存储数据。
- 贝叶斯尝试和测试的方法在数学上非常稳健。
贝叶斯回归的缺点:
- 模型的推断可能耗时。
- 如果数据集中有大量可用的数据,贝叶斯方法不值得,常规的频率主义方法能更高效地完成任务。
# 导入BayesianRidge模型类
from sklearn.linear_model import BayesianRidge
# 创建并训练模型
BayesianRidge_reg = BayesianRidge()
BayesianRidge_reg.fit(X_train, y_train)
# 模型对测试数据进行预测
y_pred = BayesianRidge_reg.predict(X_test)
# 预测交叉验证分数
cv_BayesianRidge = cross_val_score(estimator=BayesianRidge_reg, X=X_train, y=y_train, cv=10)
# 计算调整后的R平方
r2 = BayesianRidge_reg.score(X_test, y_test)
# 观测值的数量是沿着轴0的形状
n = X_test.shape[0]
# 特征的数量(预测器,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R平方公式
BayesianRidge_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
BayesianRidge_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
BayesianRidge_R2 = BayesianRidge_reg.score(X_test, y_test)
BayesianRidgeCV_R2 = cv_BayesianRidge.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 6))
print('R2:', round(BayesianRidge_reg.score(X_test, y_test), 6))
print('Adjusted R2:', round(BayesianRidge_adjusted_r2, 6))
print("Cross Validated R2:", round(cv_BayesianRidge.mean(), 6))
RMSE: 4.64904
R2: 0.709936
Adjusted R2: 0.682611
Cross Validated R2: 0.689958
# 导入必要的库
import matplotlib.pyplot as plt
import seaborn as sns
# 设置图形大小
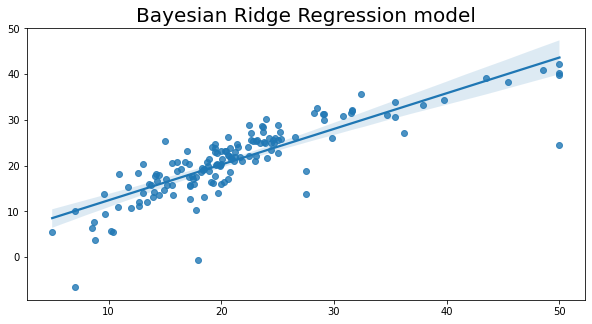
plt.figure(figsize=(10, 5))
# 绘制回归图
sns.regplot(x=y_test, y=y_pred)
# 设置图形标题和字体大小
plt.title('Bayesian Ridge Regression model', fontsize=20)
Text(0.5, 1.0, 'Bayesian Ridge Regression model')
13. 模型评估
13.1 创建新的数据框架
# 定义一个列表models,其中包含了多个元组,每个元组代表一个模型的名称和相关指标
models = [('线性回归', lm_RMSE, lm_R2, lm_adjusted_r2, lmCV_R2),
('随机森林回归', rf_RMSE, rf_R2, rf_adjusted_r2, rfCV_R2),
('线性回归(VIF)', lm2_RMSE, lm2_R2, lm2_adjusted_r2, lm2CV_R2),
('随机森林回归(VIF)', rf2_RMSE, rf2_R2, rf2_adjusted_r2, rf2CV_R2),
('随机森林回归(RFE)', rf_pipeline_RMSE, rf_pipeline_R2, rf_pipeline_adjusted_r2, rf_pipelineCV_R2),
('岭回归', lasso_RMSE, lasso_R2, lasso_adjusted_r2, lassoCV_R2),
('Lasso回归', ridge_RMSE, ridge_R2, ridge_adjusted_r2, ridgeCV_R2),
('贝叶斯岭回归', BayesianRidge_RMSE, BayesianRidge_R2, BayesianRidge_adjusted_r2, BayesianRidgeCV_R2),
]
# 创建一个名为predictions的数据框,用于存储模型的预测结果
# 数据框包含以下列:Model(模型名称)、RMSE(均方根误差)、R2 Score(R2得分)、Adjusted R2 Score(调整后的R2得分)、Cross Validated R2 Score(交叉验证的R2得分)
predictions = pd.DataFrame(data = models, columns=['Model', 'RMSE', 'R2 Score', 'Adjusted R2 Score', 'Cross Validated R2 Score'])
predictions
| Model | RMSE | R2 Score | Adjusted R2 Score | Cross Validated R2 Score | |
|---|---|---|---|---|---|
| 0 | Linear Regression | 4.638690 | 0.711226 | 0.684023 | 0.687535 |
| 1 | Random Forest Regressor | 3.329100 | 0.851262 | 0.837251 | 0.817071 |
| 2 | Linear Regression VIF | 5.457282 | 0.600313 | 0.580884 | 0.606042 |
| 3 | Random Forest Regressor VIF | 4.406752 | 0.739382 | 0.726713 | 0.755377 |
| 4 | Random Forest Regressor RFE | 3.324301 | 0.851691 | 0.837720 | 0.816235 |
| 5 | Ridge Regression | 4.876996 | 0.680793 | 0.650723 | 0.673983 |
| 6 | Lasso Regression | 4.640288 | 0.711027 | 0.683805 | 0.688212 |
| 7 | Bayesian Ridge Regression | 4.649040 | 0.709936 | 0.682611 | 0.689958 |
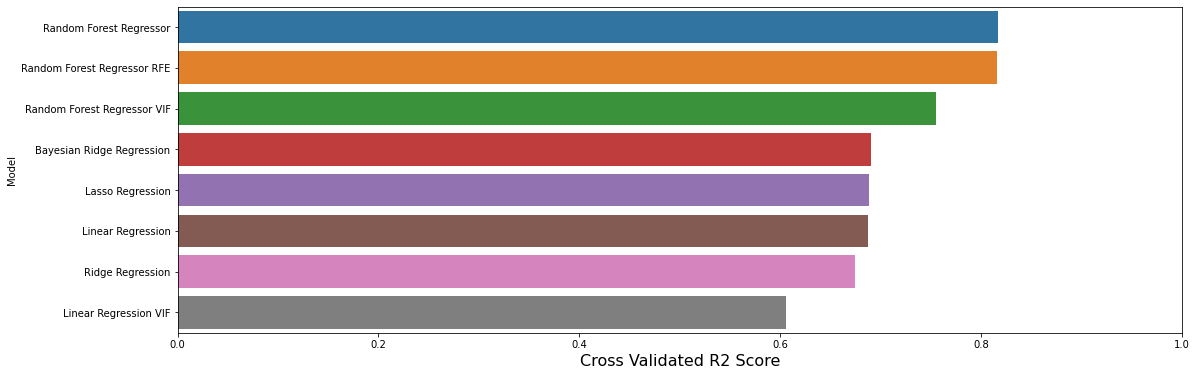
结果可能会有些令人惊讶。
- 看起来使用VIF方法进行简单特征删除导致了更糟糕的结果!
- 即使一些更健壮的模型也没有比最简单的线性回归表现更好。
结论是什么?
- VIF并不像我们预期的那样简单。
- “更好”的模型并不总是更好。
- 可能我们应该更加努力以获得更好的结果(例如通过参数调整)。
13.2 可视化模型性能
# 导入必要的库已经完成,不需要再添加import语句
# 创建一个画布和一个子图
f, axe = plt.subplots(1,1, figsize=(18,6))
# 按照交叉验证R2得分进行排序
predictions.sort_values(by=['Cross Validated R2 Score'], ascending=False, inplace=True)
# 使用sns库中的barplot函数绘制条形图,x轴为交叉验证R2得分,y轴为模型名称,数据来源为predictions,子图为axe
sns.barplot(x='Cross Validated R2 Score', y='Model', data = predictions, ax = axe)
# 设置x轴标签为"Cross Validated R2 Score",字体大小为16
axe.set_xlabel('Cross Validated R2 Score', size=16)
# 设置y轴标签为"Model"
axe.set_ylabel('Model')
# 设置x轴范围为0到1.0
axe.set_xlim(0,1.0)
# 显示图形
plt.show()
14. 使用GridSearchCV进行超参数调优
超参数调整是在构建机器学习模型时调整参数元组的过程。这些参数是由我们定义的。机器学习算法不会学习这些参数。这些参数可以在不同的步骤中进行调整。
GridSearchCV是一种从给定的参数网格中找到最佳超参数值的技术。它本质上是一种交叉验证技术。必须输入模型以及参数。在提取最佳参数值后,进行预测。
GridSearchCV识别的“最佳”参数实际上是在您的参数网格中包含的参数的最佳值。
14.1 调整后的岭回归
# 导入PolynomialFeatures类
from sklearn.preprocessing import PolynomialFeatures
# PolynomialFeatures是通过将现有特征提升到指数来创建的特征。
# 例如,如果一个数据集有一个输入特征X,
# 那么多项式特征将是添加一个新的特征(列),其中的值是通过对X的值进行平方计算得到的,例如X^2。
# 定义步骤列表,其中包含两个步骤:'poly'和'model'
steps = [
('poly', PolynomialFeatures(degree=2)), # 使用degree=2创建二次多项式特征
('model', Ridge(alpha=3.8, fit_intercept=True)) # 使用Ridge回归模型,设置alpha=3.8和fit_intercept=True
]
# 创建Pipeline对象,将步骤列表作为参数传递给Pipeline构造函数
ridge_pipe = Pipeline(steps)
# 使用训练数据X_train和y_train来训练Pipeline对象
ridge_pipe.fit(X_train, y_train)
# 使用训练好的模型对测试数据X_test进行预测
y_pred = ridge_pipe.predict(X_test)
# 导入GridSearchCV类
from sklearn.model_selection import GridSearchCV
# 定义alpha参数的取值范围
alpha_params = [{'model__alpha': list(range(1, 15))}]
# 创建GridSearchCV对象,使用ridge_pipe作为模型,alpha_params作为参数范围,cv=10表示使用10折交叉验证
clf = GridSearchCV(ridge_pipe, alpha_params, cv=10)
# 使用训练数据拟合和调优模型
clf.fit(X_train, y_train)
# 模型对测试数据进行预测
y_pred = BayesianRidge_reg.predict(X_test)
# 输出最佳参数组合及其对应的性能表现
print(clf.best_params_)
{'model__alpha': 12}
# 预测交叉验证分数
cv_Ridge3 = cross_val_score(estimator=clf, X=X_train, y=y_train, cv=10)
# 计算调整后的R平方
r2 = clf.score(X_test, y_test)
# 观测值的数量是沿着轴0的形状
n = X_test.shape[0]
# 特征的数量(预测器,p)是沿着轴1的形状
p = X_test.shape[1]
# 调整后的R平方公式
Ridge3_adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)
Ridge3_RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred))
Ridge3_R2 = clf.score(X_test, y_test)
Ridge3CV_R2 = cv_Ridge3.mean()
print('RMSE:', round(np.sqrt(metrics.mean_squared_error(y_test, y_pred)), 6))
print('R2:', round(clf.score(X_test, y_test), 6))
print('Adjusted R2:', round(Ridge3_adjusted_r2, 6))
print("Cross Validated R2:", round(cv_Ridge3.mean(), 6))
RMSE: 4.64904
R2: 0.827825
Adjusted R2: 0.811606
Cross Validated R2: 0.845011
14.2 可视化模型性能
# 定义了一个列表models2,其中包含了多个元组
# 每个元组包含了一个模型的名称和相关的评估指标
# 评估指标包括 Ridge3_RMSE(均方根误差)、Ridge3_R2(R平方值)、Ridge3_adjusted_r2(调整后的R平方值)和Ridge3CV_R2(交叉验证的R平方值)
models2 = [('Tuned Ridge Regression', Ridge3_RMSE, Ridge3_R2, Ridge3_adjusted_r2, Ridge3CV_R2)]
# 创建一个DataFrame对象predictions2,包含多个列
# 列名分别为'Model', 'RMSE', 'R2 Score', 'Adjusted R2 Score', 'Cross Validated R2 Score'
# data参数为models2,即数据来源为models2
predictions2 = pd.DataFrame(data = models2, columns=['Model', 'RMSE', 'R2 Score', 'Adjusted R2 Score', 'Cross Validated R2 Score'])
predictions2
| Model | RMSE | R2 Score | Adjusted R2 Score | Cross Validated R2 Score | |
|---|---|---|---|---|---|
| 0 | Tuned Ridge Regression | 4.64904 | 0.827825 | 0.811606 | 0.845011 |
# 使用pd.concat()函数将predictions和predictions2两个数据合并为一个数据
# 参数ignore_index=True表示忽略原始数据的索引,重新生成新的索引
# 参数sort=False表示不对合并后的数据进行排序
result = pd.concat([predictions, predictions2], ignore_index=True, sort=False)
result
| Model | RMSE | R2 Score | Adjusted R2 Score | Cross Validated R2 Score | |
|---|---|---|---|---|---|
| 0 | Random Forest Regressor | 3.329100 | 0.851262 | 0.837251 | 0.817071 |
| 1 | Random Forest Regressor RFE | 3.324301 | 0.851691 | 0.837720 | 0.816235 |
| 2 | Random Forest Regressor VIF | 4.406752 | 0.739382 | 0.726713 | 0.755377 |
| 3 | Bayesian Ridge Regression | 4.649040 | 0.709936 | 0.682611 | 0.689958 |
| 4 | Lasso Regression | 4.640288 | 0.711027 | 0.683805 | 0.688212 |
| 5 | Linear Regression | 4.638690 | 0.711226 | 0.684023 | 0.687535 |
| 6 | Ridge Regression | 4.876996 | 0.680793 | 0.650723 | 0.673983 |
| 7 | Linear Regression VIF | 5.457282 | 0.600313 | 0.580884 | 0.606042 |
| 8 | Tuned Ridge Regression | 4.649040 | 0.827825 | 0.811606 | 0.845011 |
# 创建一个图形对象和一个坐标轴对象
f, axe = plt.subplots(1,1, figsize=(18,6))
# 按照'Cross Validated R2 Score'列的值进行降序排序
result.sort_values(by=['Cross Validated R2 Score'], ascending=False, inplace=True)
# 使用条形图显示数据,x轴为'Cross Validated R2 Score',y轴为'Model'
sns.barplot(x='Cross Validated R2 Score', y='Model', data = result, ax = axe)
# 设置x轴标签为'Cross Validated R2 Score',字体大小为16
axe.set_xlabel('Cross Validated R2 Score', size=16)
# 设置y轴标签为'Model'
axe.set_ylabel('Model')
# 设置x轴的范围为0到1.0
axe.set_xlim(0,1.0)
# 显示图形
plt.show()

我们可以看到,调整后的岭回归甚至在考虑交叉验证的R2得分时也优于随机森林回归器RFE!
但是 - 这显然不是结束。我们可以调整其他模型 😉 这是机器学习中永无止境的故事,这显然是令人兴奋的部分 😉
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 机器学习--主成分分析 PCA
- mysql
- Python爬虫 - 网易云音乐下载
- Ubuntu:VS Code上C++的环境配置
- 鸿蒙开发实战-手写文心一言AI对话APP
- 华清远见作业第十四天
- 基于Java Web贫困认定管理平台论文
- vu3+ts:mousedown mousemove mouseup 与 click事件冲突的解决办法
- 【flink番外篇】9、Flink Table API 支持的操作示例(5)- 表的列操作
- JAVA学习中涉及的Maven、JDK安装以及黑马SpringBoot源项目运行时存在的异常问题的解决