三维旋转之四元数

先来一道问题

问

绕方向（nx，ny，nz）旋转m角的旋转矩阵用四元数表示(_ ,_ ,_ ,_)^T

答

q =
?cos( θ / 2 )
? nx?sin( θ/2 ) ?
?ny?sin( θ/2 )
? nz?sin( θ/2 ) ?

?=
(cos( θ/2 ) ,nx?sin( θ/2 ) ,ny?sin( θ/2 ) ,nz?sin( θ/2 ))^T

---

注:
如果你是手机党 , 上面的公式你可能会觉得别扭,这是因为手机不能像电脑端显示的那么全,其他的电脑端和手机端就一致了! 请看如下图片: 这才是公式全貌!

---

题目给出的四个空是四元数的具体分量。绕轴 (nx,ny,nz) 旋转角度 θ 的四元数 q 可以表示为四个分量：

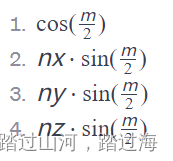
注:把图片里的m,改成θ
这样的表示方式是把四元数视为一个四维向量，其中第一个分量是实部，其余三个是虚部。

关于四元数

在 3D 图形编程中，使用四元数（quaternions）来表示旋转是非常高效和常见的。四元数避免了万向节锁问题（gimbal lock），并且对于插值和组合旋转非常有效。

给定一个旋转轴 (nx,ny,nz) 和一个旋转角度 m（通常以弧度表示,比如θ），四元数 $q$ 可以表示为:

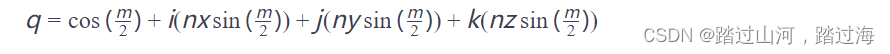
?其中 ,$cos(\theta /2)$是实部 , $i$,$j$,$k$是四元数的虚部单位。
?

四元数的数学本质与原理

教程,可以直接定位到 $02:52$

四元数与编程

在实际应用中，你通常会使用一个四元数库，这样你就不需要直接处理这些数学细节。例如，在$C++$ and $Opengl$中，如果你使用了像$GLM$这样的数学库，你可以这样创建一个四元数来表示旋转：

#include <glm/glm.hpp>
#include <glm/gtc/quaternion.hpp>

// 定义旋转轴和角度
glm::vec3 axis(nx, ny, nz);
float angle = m; // 弧度

// 创建四元数
glm::quat myQuaternion = glm::angleAxis(angle, axis);

补充一点,右上角的那个小t表示什么?

那个小写的 “T” 在这个上下文中代表 “转置”（Transpose）。当你把四元数或任何向量写成行向量的形式（水平排列），在其后加上 “T” 意味着你将其转换成列向量（垂直排列）。这是线性代数中的一个标准表示方法。

在计算机图形学和矩阵运算中，这种表示方法很常见，特别是在处理转换矩阵和向量时。