算法学习记录：位运算

前言：

? 算法学习记录不是算法介绍，本文记录的是从零开始的学习过程（见到的例题，代码的理解……），所有内容按学习顺序更新，而且不保证正确，如有错误，请帮助指出。

学习工具：蓝桥OJ，LeetCode

目录

前言：

正文：

背景知识：

什么是位运算：

简单理解：

&:

|:

^:

<<:?

>>:

位运算的妙用：

1.判断数字奇偶性

2.获取二进制数的某一位

3.修改二进制数的某一位

4.快速判断一个数字是否为2的幂次方

5.获取二进制位中最低位1

用位运算解决问题（更新中）：

1.快速求幂次：

蓝桥OJ 2230：快速幂

2.枚举子集：

蓝桥OJ 4360：串变换

3.倍增算法：

---

正文：

背景知识：

? 你已经学过原码、反码、补码这样的基础知识。

? 你可以进行进制换算。

? 你了解过一定的程序的机器级表示。（CSAPP 第三章）

一些基础知识可以帮助理解，但不影响编程中位运算的学习。

什么是位运算：

数字在计算机中以二进制的形式存储，直接对二进制位进行的运算，就是位运算。

简单理解：

? C/C++的代码经过编译器转换和优化得到汇编代码。

因为计算机只能理解二进制数字，所以，十进制数字会被转换成二进制数字。

经过存储、运算等操作后，再变成人能看懂的十进制数字输出。

因此，位运算不仅可以提高效率，也有一些妙用，帮助我们解决复杂问题。

&:

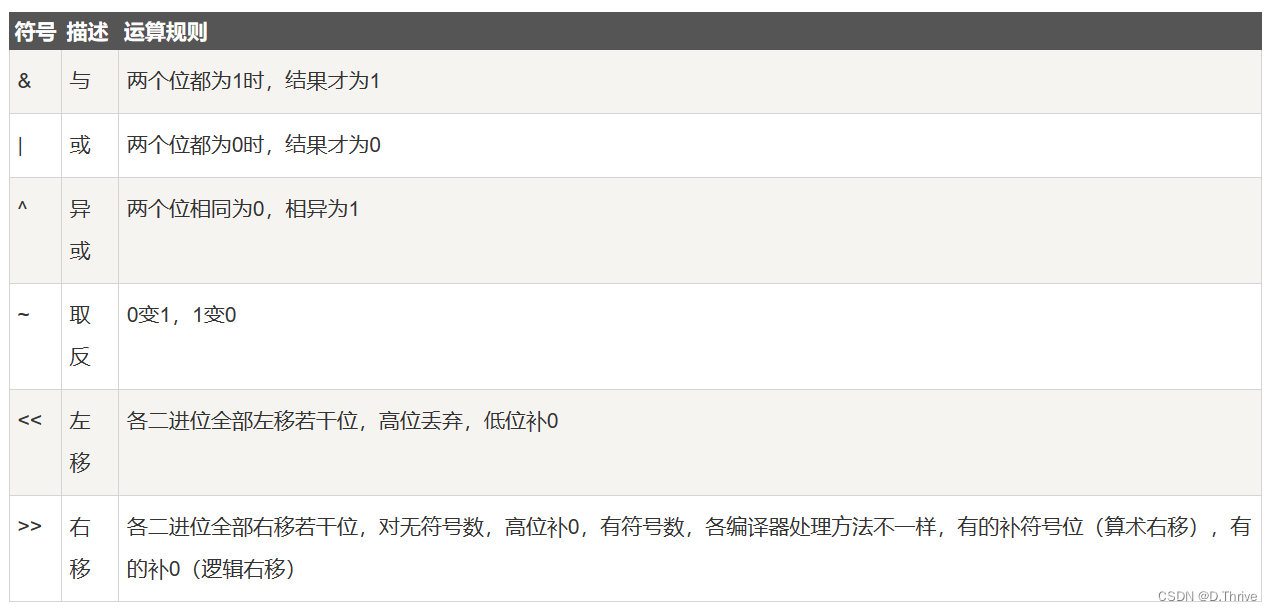
与运算：”两个位都为1时，结果才为1“，默认是对最小的那一位，比如：

十进制数（7） =?二进制数（111）:

8&1表示的意思就是：二进制111的最小位是不是1，111最小位是1，运算结果就是1（ true）

|:

0或1，只要有一个1，运算结果就是1（true）。

^:

异或运算：”相同为1，相异为0“

<<:?

箭头向左，表示左移

对于有符号整数来说，这里的左移就是逻辑左移，x<<i相当于十进制乘以2^i

>>:

箭头向右，表示右移

对于有符号整数来说，这里的右移是逻辑右移，x>>i相当于十进制除以 2^i

位运算的妙用：

1.判断数字奇偶性

公式：x&1

2.获取二进制数的某一位

公式：x >> j & 1

3.修改二进制数的某一位

公式：

x || (1 << j)? ? 修改位1

x & ~(1 << j)? ? 修改为0

4.快速判断一个数字是否为2的幂次方

公式：x & (x - 1)

5.获取二进制位中最低位1

公式：lowbit(x) = x & - x

用位运算解决问题（更新中）：

1.快速求幂次：

蓝桥OJ 2230：快速幂

/*倍增求快速幂*/

#include<bits/stdc++.h>
using namespace std;
#define mod 998244353
#define ll long long
int main(){
	ll b,p,k;
	cin >> b >> p >> k;
	ll s=1;
	while(p)
	{
		if(p&1)s = s * b % k;
		
		b = b * b % k;p >>= 1;
	}
	cout << s <<endl;
	
	return 0;
	
}

求 b ^ p % k ，一个十进制数总可以写成二进制，例如：求?2 ^ 7?，下图可以帮助理解：

2.枚举子集：

蓝桥OJ 4360：串变换

#include<bits/stdc++.h>

using ll = long long;
using ld = long double;

using namespace std;
struct Q {
	int op,x,y;
};

void solve(const int &Case) {
	int n;cin >> n;
	string s,t;
	cin >> s >> t;
	int k;cin >> k;
	vector<Q>que(k);
	for(auto &[op,x,y]:que)cin >> op >> x >> y;
	for(int S = 0; S < 1<< k; S++) {// 枚举子集
		vector<int>tmp;
		for(int i = 0;i < k;i ++) {
			if(S >> i & 1)tmp.push_back(i);
		}
		do{
			string now = s;
			for(auto i :tmp) {
				const auto &[op,x,y] = que[i];
				if( op == 1) {
					s[x] = char('0' + (s[x] - '0' + y) % 10);
			}else {
					swap(s[x],s[y]);
				}
	    	}
			if(now == t) {
				cout << "Yes\n";
				return ;
			}	
			
    	}while(next_permutation(tmp.begin(),tmp.end()));  // 枚举排列
	}
    cout << "No\n";
}


int main() {
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	solve(1);
	
	return 0;
}

枚举子集通常和枚举排列一起使用。

分别是：每一个子元素的有无、每一个子元素的排列顺序 ， 枚举出了它们的所有可能情况

枚举子集的代码也不好从直觉上理解，但是将原数转换成二进制再看会好理解的多。

3.倍增算法：

这方面的用途广，会作为算法的代码实现方式出现。