最小生成树（Java实现）

一、Prim算法

? ? ? ? Prim算法基本思想为：从联通网络 N={V,E}中某一顶点 v0 出发，此后就从一个顶点在 S 集中， 另一个顶点不在 S 集中的所有顶点中选择出权值最小的边，把对应顶点加入到 S 集 中， 直到所有的顶点都加入到 S 集中为止。

原始图：

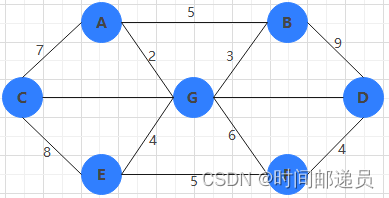
最小生成树：

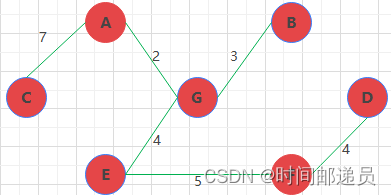
package algorithm;

public class prim {
    public static void main(String[] args) {
        char[] vertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
        int num = vertex.length;
        int[][] edge = {//10000表示两个顶点不通
                {10000, 5, 7, 10000, 10000, 10000, 2},
                {5, 10000, 10000, 9, 10000, 10000, 3},
                {7, 10000, 10000, 10000, 8, 10000, 10000},
                {10000, 9, 10000, 10000, 10000, 4, 10000},
                {10000, 10000, 8, 10000, 10000, 5, 4},
                {10000, 10000, 10000, 4, 5, 10000, 6},
                {2, 3, 10000, 10000, 4, 6, 10000}};

        MGraph mGraph = new MGraph(num);
        MinTree minTree = new MinTree();
        minTree.creatGraph(mGraph, num, vertex, edge);
        minTree.showGraph(mGraph);
        minTree.prim(mGraph, 0);
    }
}


class MGraph {
    int num; //顶点的个数
    char[] vertex; //顶点的元素
    int[][] edge; //存放边

    public MGraph(int num) { //构造器
        this.num = num;
        vertex = new char[num];
        edge = new int[num][num];
    }
}

class MinTree {
    //创建图
    public void creatGraph(MGraph mGraph, int num, char[] vertex, int[][] edge) {
        for (int i = 0; i < num; i++) {
            mGraph.vertex[i] = vertex[i]; //添加每个顶点的名字
            for (int j = 0; j < num; j++) {
                mGraph.edge[i][j] = edge[i][j]; //添加各个城市之间直接相连的边的权值
            }
        }
    }

    //普利姆算法
    public void prim(MGraph mGraph, int node) {
        int[] vis = new int[mGraph.num]; //用于标记遍历过的节点
        vis[node] = 1; //将当前节点标记为1表示已访问
        //用来记录最小路径中两个节点的下标
        int index1 = -1;
        int index2 = -1;
        for (int k = 1; k < mGraph.num; k++) { //若有n个节点 则有n - 1 条边
            int minSide = Integer.MAX_VALUE; //遍历与之比较 找到最小的路径
            for (int i = 0; i < mGraph.num; i++) {
                for (int j = 0; j < mGraph.num; j++) {
                    if (vis[i] == 1 && vis[j] == 0 && mGraph.edge[i][j] < minSide) {
                        minSide = mGraph.edge[i][j]; //最短边上的权值
                        //最短边的两个顶点
                        index1 = i;
                        index2 = j;
                    }
                }
            }
            //从第内层for循环出来后，表示找到一条最短边
            System.out.println("边<" + mGraph.vertex[index1] + "," + mGraph.vertex[index2] + ">权值：" + minSide);
            vis[index2] = 1; //将最内层与已访问节点路径最短的节点设置为已访问
        }
    }

    //输出初始图
    public void showGraph(MGraph mGraph) {
        for (int[] arr : mGraph.edge) {
            for (int element : arr) {
                System.out.print(element + " ");
            }
            System.out.println();
        }
    }
}

二、Kruskal算法

????????kruskal其基本思想为：设有一个有 N 个顶点的联通网络 N={V,E}，初始时建立一个只有 N 个顶点且没有边的非连通图 T，T 中每个顶点都看作是一个联通分支，从边集 E 中选择出权值最小的边且该边的两个端点不在一个联通分支中，则把该边加入到 T 中，否则就再从E新选择一条权值最小的边，直到所有的顶点都在一个联通分支中为止。

package algorithm;

import java.util.*;
/*
1. 定义一个并查集类，用于判断两个顶点是否属于同一个连通分量
2. 对图中的所有边按照权重进行排序
3. 遍历排序后的边，如果边的两个顶点不属于同一个连通分量，则将这条边加入最小生成树中，并将这两个顶点所在的连通分量合并
4. 重复步骤3，直到最小生成树中的边数等于顶点数减1
*/

class UnionFind {
    int[] parent;//存储每个结点的前驱结点
    int[] rank;//树的高度

    public UnionFind(int n) {
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;//每个结点的上级都是自己
            rank[i] = 1;//每个结点构成的树的高度为1
        }
    }

    public int find(int x) {
        if (parent[x] == x) {//递归出口：x的上级为 x本身，即 x为根结点
            return x;
        }
        return parent[x] = find(parent[x]);//此代码相当于先找到根结点 rootx，然后 parent[x]=rootx
    }

    public boolean union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX == rootY) {
            return false;
        }
        if (rank[rootX] > rank[rootY]) {
            parent[rootY] = rootX;
        } else if (rank[rootX] < rank[rootY]) {
            parent[rootX] = rootY;
        } else {
            parent[rootY] = rootX;
            rank[rootX]++;
        }
        return true;
    }
}

class Edge implements Comparable<Edge> {
    int from;
    int to;
    int weight;

    public Edge(int from, int to, int weight) {
        this.from = from;
        this.to = to;
        this.weight = weight;
    }

    @Override
    public int compareTo(Edge other) {
        return this.weight - other.weight;
    }
}

public class KruskalAlgorithm {
    public static void main(String[] args) {
        int[][] graph = {
                {0, 1, 5},
                {0, 2, 7},
                {0, 6, 2},
                {1, 6, 3},
                {1, 3, 9},
                {2, 4, 8},
                {3, 5, 4},
                {4, 5, 5},
                {4, 6, 4},
                {5, 6, 6},
        };
        List<Edge> edges = new ArrayList<>();
        for (int[] edge : graph) {
            edges.add(new Edge(edge[0], edge[1], edge[2]));
        }
        Collections.sort(edges);
        UnionFind uf = new UnionFind(graph.length);
        List<Edge> result = new ArrayList<>();
        for (Edge edge : edges) {
            if (uf.union(edge.from, edge.to)) {
                result.add(edge);
            }
        }
        System.out.println("最小生成树的边为：");
        for (Edge edge : result) {
            System.out.println(edge.from + " - " + edge.to + " : " + edge.weight);
        }
    }
}

原始图：

最小生成树：