【算法分析与设计】和为k的子数组

目录

问题

示例

方案一：

思路：

算法设计

代码实现

运行结果：

方案二(调优)

思路（前缀和）

算法设计

示意图

代码实现

?运行结果

---

问题

给你一个整数数组?nums?和一个整数?k?，请你统计并返回?该数组中和为?k?的子数组的个数?。

子数组是数组中元素的连续非空序列。

示例

示例 1：

输入：nums = [1,1,1], k = 2
输出：2

示例 2：

输入：nums = [1,2,3], k = 3
输出：2

方案一：

思路：

暴力破解

算法设计

两层for循环 穷举所有示例，找到符合的count++

算法示意图

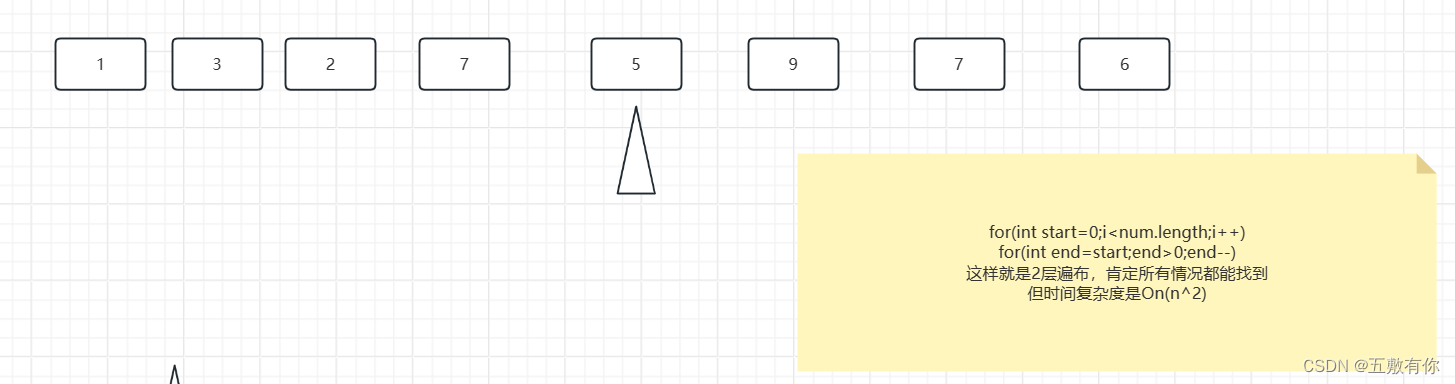
代码实现

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.length; ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
}

运行结果：

居然没有超时，超乎我的想象

?但我知道肯定不能这么做。。。寻求优化

方案二(调优)

思路（前缀和）

使用前缀和的方法可以解决这个问题，因为我们需要找到和为k的连续子数组的个数。

通过计算前缀和，我们可以将问题转化为求解两个前缀和之差等于k的情况。

算法设计

用一个Map集合，然后将key值为找到的前缀和，然后都存到Map中，通过不同的前缀和相减得到某个区间的一段和。

每算一次前缀和，就判断是否在map中（count是看有多少个满足条件的前缀和）

? ? ? ? 在：返回值count+=map.get(key)?然后更新这个前缀和在map中的count +1

? ? ? ? 不在：更新前缀和在map中的count+1

最后返回count即可

示意图

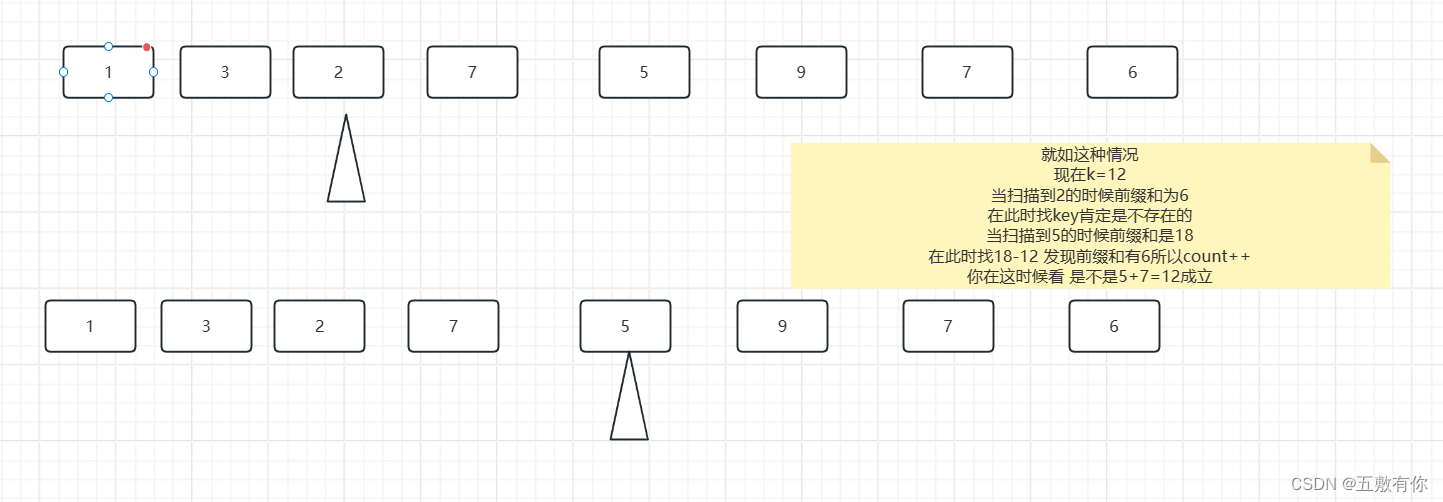
代码实现

public class Solution {
   public static int subarraySum(int[] nums, int k) {
        int count = 0;
        int sum = 0;
        Map<Integer, Integer> map = new HashMap<>();
        //key 为前缀和 value为count
        map.put(0, 1); // 初始化前缀和为0的次数为1


        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            //关键在这，sum-k就是在找另外一段前缀和是否存在
            if (map.containsKey(sum - k)) {

                count += map.get(sum - k);
            }
            map.put(sum, map.getOrDefault(sum, 0) + 1);
        }

        return count;
    }
}

?运行结果

确实快噢~?