相机坐标系如何转换到世界坐标系。

问题描述：相机坐标系如何转换到世界坐标系。

问题解答：

相机坐标系的定义：相机坐标系是以相机为基准建立的坐标系。它通常将相机的光学中心作为原点，相机的光轴为Z轴，X轴和Y轴与图像平面平行，与光轴垂直，形成一个右手坐标系。

世界坐标系的定义：世界坐标系通常是以某个固定的参考点、参考物体或参考方向为基准建立的。这个参考点可以是任何合适的选择，具体取决于应用的领域和需求。例如，在机器人学中，世界坐标系的原点可以选择为机器人基座的中心，或者是机器人末端执行器的中心。在地理信息系统中，世界坐标系的原点通常选择为地球的某个地理位置，例如经纬度为 (0, 0) 的点。

我理解的相机坐标系转换到世界坐标系的过程就是手眼标定过程，手指的是机械臂，眼指的是相机。

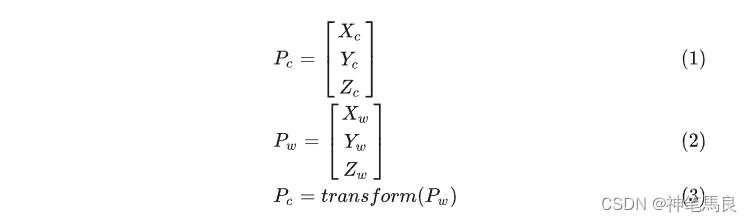
假设物体在相机坐标系中的坐标为，物体在世界坐标系中的坐标为。则从相机坐标系转换到世界坐标系的转换函数即为transform()

由本科学习到的线性代数知识，一个物体坐标左乘一个矩阵的几何意义是，这个物体进行旋转。物体坐标加上一个向量，即为平移。

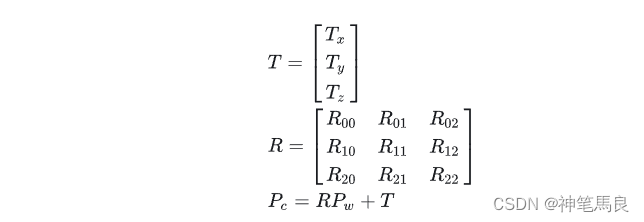
假设平移向量是T，旋转矩阵是R，因此转换函数即为transform()即为

线性代数中常把非齐次坐标转换为齐次坐标，因此，上述转换函数可以改成

上面的这个矩阵就是众所周知的外参矩阵。