2路归并排序-自顶向下递归
Description
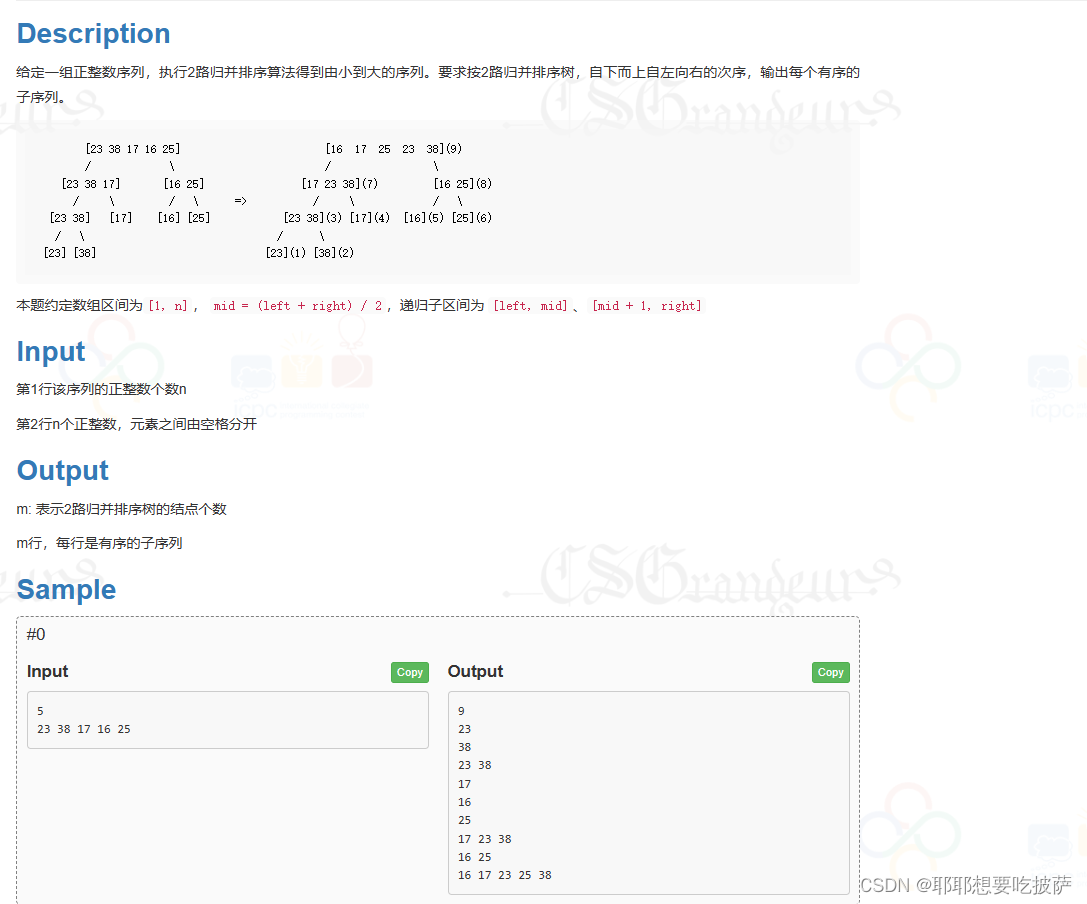
给定一组正整数序列,执行2路归并排序算法得到由小到大的序列。要求按2路归并排序树,自下而上自左向右的次序,输出每个有序的子序列。
[23 38 17 16 25] [16 17 25 23 38](9)
/ \ / \
[23 38 17] [16 25] [17 23 38](7) [16 25](8)
/ \ / \ => / \ / \
[23 38] [17] [16] [25] [23 38](3) [17](4) [16](5) [25](6)
/ \ / \
[23] [38] [23](1) [38](2)本题约定数组区间为[1, n],?mid = (left + right) / 2,递归子区间为?[left, mid]、[mid + 1, right]
Input
第1行该序列的正整数个数n
第2行n个正整数,元素之间由空格分开
Output
m: 表示2路归并排序树的结点个数
m行,每行是有序的子序列
Sample
#0
Input
Copy
5 23 38 17 16 25
Output
Copy
9 23 38 23 38 17 16 25 17 23 38 16 25 16 17 23 25 38
本题分析:
这题不只是归并排序,所以我们得分析一下题目意思,还有他的输入输出。
首先整体上排序需要用到归并排序,其次我们自顶向下的时候不是会把长的数组变成一段一段小的吗,他就是把他变成了一个这样的节点意思。然后从最下面的节点开始输出,我们来画一下他的输出顺序
本题意思就是我们分出节点之后然后将他每个节点排序好后输出,我是这么理解的。
然后怎么样将这种树输出呢,首先我们就不看数组了,将其看出一个一个节点,如果我们将层序遍历时的先左子节点变成先右子节点呢?
是不是我们的顺序就是9 8 7 6 5 4 3 2 1,(顺序看右图画的数字)。然后我们输出顺序是1,2,3,4,5,6,那是不是可以把他放进堆里面,堆|987654321,然后取出来就是123456789,这样我们就可以完成这道题的输出了
思路:
? ?1.节点里面存什么:
? 我的想法是我不存分段的数组,就是一个节点里面存23 36 17 16 25,另一个节点存23 38 17这样的。我存他们的下标起始点和终点,就是1到5,然后另一个节点就是1到3
本题要求:
本题约定数组区间为[1, n],?mid = (left + right) / 2,递归子区间为?[left, mid]、[mid + 1, right]
主要要用到归并排序,归并排序自顶向下递归的时候不就需要起始点和终点吗

? ? ?2.建立树
还是老习惯,我喜欢先建立跟节点,然后插入(其实主要是当时好像忘记怎么建树了)
建立根

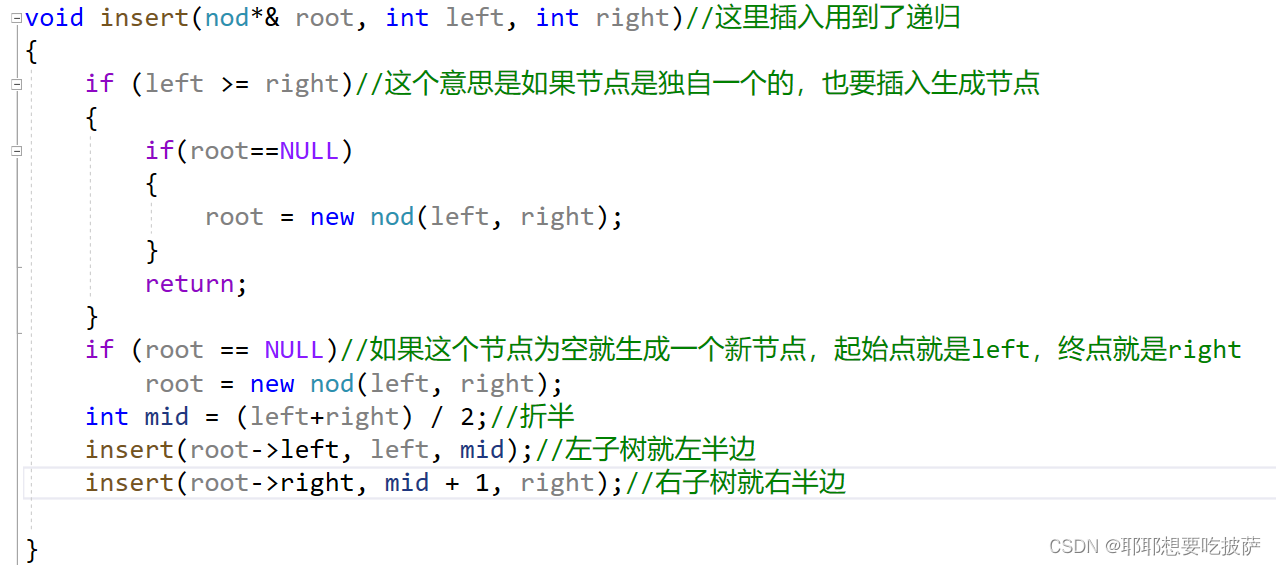
插入新节点
3.层序遍历加堆放入节点,完成输出倒转就是987654321变成123456789

4.从节点1开始遍历然后排序并且输出
本题要求的是输出排好序的那个节点,里面用了归并排序的方法
? ?1.第一部我调用堆然后从1开始拿出节点

? ?2.然后将这个节点排好序
?

? ?3.然后输出这个节点里的排好序的元素:就是调用out函数

然后将我们的堆ss用空就好了
全部代码:
? ? ? ? 因为本人最近比较忙,所以就懒得对代码进行优化啊,美化啊,所以大家可以对上面思路部分分块的重要的代码进行理解就好了,这全部代码其实也是上面的拼接好而已啦!
#include <iostream>
#include <stack>
#include <queue>
using namespace std;
const int maxn = 1e4 + 10;
int dp[maxn];
int emerge[maxn];
int n;
struct nod
{
int s, e;//s是起始点,e是终点
nod* left, * right;//left是左子节点,right是右子节点
nod()
{
left = NULL;
right = NULL;
}
nod(int a, int b)
{
s = a;
e = b;
left = NULL;
right = NULL;
}
};
stack<nod*>ss;
void insert(nod*& root, int left, int right)//这里插入用到了递归
{
if (left >= right)//这个意思是如果节点是独自一个的,也要插入生成节点
{
if(root==NULL)
{
root = new nod(left, right);
}
return;
}
if (root == NULL)//如果这个节点为空就生成一个新节点,起始点就是left,终点就是right
root = new nod(left, right);
int mid = (left+right) / 2;//折半
insert(root->left, left, mid);//左子树就左半边
insert(root->right, mid + 1, right);//右子树就右半边
}
nod* build()
{
nod* root;//n是总共有多少个元素
root = new nod(1, n);//建立根节点,根节点在最顶所以就是最开始的1到n
int mid = (1 + n) / 2;//mid就是折半嘛
insert(root->left, 1, mid);//然后左半边
insert(root->right, mid + 1, n);//右半边
return root;
}
queue<nod*>p;
int height;
void cengxu(nod* root)
{
if (root == NULL)
return;
ss.push(root);//ss是我建立的堆
p.push(root);//p是我建立的队列,层序遍历需要用到队列嘛
while (!p.empty())//如果队列非空就进入循环
{
nod* q = p.front();//取出一个节点
p.pop();
if (q->right != NULL)//然后本题思路是先右节点,所以就如果存在就放入队列里面,并且放入堆里面
{
p.push(q->right);
ss.push(q->right);
height++;//height是我用来统计总共有几个节点的,有就+1,然后我的height初始值为1,所以上面建立根就没+1了
}
if (q->left != NULL)//然后就是左子节点,一样的操作
{
p.push(q->left);
ss.push(q->left);
height++;
}
}
}
void out(int l, int r)
{
for (int i = l; i <= r; i++)//从左边界到有边界输出
{
cout << dp[i] << " ";
}
cout << endl;
}
void emerge_sort(nod* root)
{
if (root == NULL)
return;
int left = root->s, right = root->e;//获取这个节点的起点和终点
int mid = (left + right) / 2;//折半
int i, j, k;
for (i = k = left, j = mid + 1; j <= right && i <= mid;)//这部分就是排序算法了
{ //空数组emerge[],和原顺序数组dp[],
if (dp[i] <= dp[j]) //实现思路我举个例子原数组六个树1,6,5,2,3,4,然后对半分开
emerge[k++] = dp[i++];//left指向1,right指向4,mid+1指向2,分成1,5,6 | 2,3,4
else //1<2,emerge:1 5>2,emerge:1,2 5>3,emerge:1,2,3 5>4,emerge:1,2,3,4
emerge[k++] = dp[j++]; //然后就退出这个循环了
}
while (i <= mid) //前面部分还没放完,但是第二部分放完了,那就把前面部分都放在后面部分
{ //emerge:1,2,3,4,5,6
emerge[k++] = dp[i++];
}
while (j <= right) //这个意思也一样,但是我举得例子里面他已经放完了就不
{
emerge[k++] = dp[j++];
}
for (int m = left; m <= right; m++)//然后我们将emerge的数组放进dp里面,覆盖掉之前没排序的
{
dp[m] = emerge[m];
}
out(left, right);//然后这里我们就输出一下这个节点
}
int main()
{
while (cin >> n)
{
for (int i = 1; i <= n; i++)
{
cin >> dp[i];
}
height = 1;
nod* root = build();
cengxu(root);
cout << height << endl;
while (!ss.empty())
{
emerge_sort(ss.top());
ss.pop();
}
}
}好久没更了,为什么更新这个因为确实有点难想他的输出顺序,我看了别人的代码感觉思路有点复杂,所以我觉得就层序遍历变通一下,变成先右子节点再左子节点然后用堆将他反过来就好了
快期末了,祝大家都有个好的成绩,过个好年!!!
白白
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 大学生体质测试管理 毕业设计源码42047
- python的 read, readlines,readline 有何异同,读取文件的时候用哪个好?怎么选择。
- ssm超市销售管理系统(开题+源码)
- 【操作系统】实验名称: 实验五 文件系统
- Keepalived双机热备
- chatglm部署问题
- Linux终端常见用法总结
- 每日一题——LeetCode1252.奇数值单元格的数目
- 网络互通--三层交换机配置
- 静态HTTP:构建高效、可扩展的Web应用程序的基础