OpenCV改变图像的对比度和亮度！

目标

在本教程中，您将学习如何：

• 访问像素值
• 用零初始化矩阵
• 了解?cv：：saturate_cast?的作用以及它为什么有用
• 获取有关像素转换的一些很酷的信息
• 在实际示例中提高图像的亮度

理论

注意

下面的解释属于Richard Szeliski的《计算机视觉：算法和应用》一书

图像处理

• 一般图像处理算子是获取一个或多个输入图像并生成输出图像的函数。
• 图像转换可以看作是：
  • 点运算符（像素变换）
  • 邻里（基于区域）运营商

像素变换

• 在这种图像处理转换中，每个输出像素的值仅取决于相应的输入像素值（以及可能收集的一些全局收集的信息或参数）。
• 此类运算符的示例包括亮度和对比度调整以及颜色校正和转换。

亮度和对比度调整

• 两个常用的点过程是乘法和加法，具有常数：

  \[g（x） = \alpha f（x） + \beta\]

• 参数 \（\alpha > 0\） 和 \（\beta\） 通常称为增益和参数;有时据说这些参数分别控制α>0和亮度。

• 您可以将 \（f（x）\） 视为源图像像素，将 \（g（x）\） 视为输出图像像素。然后，更方便的是，我们可以将表达式写成：

  \[g（i，j） = \alpha \cdot f（i，j） + \beta\]

  其中 \（i\） 和 \（j\） 表示像素位于第 i?行和第 j?列中。

法典

C++爪哇岛蟒

解释

C++爪哇岛蟒

• 我们使用?cv：：imread?加载图像并将其保存在 Mat 对象中：

CommandLineParser parser（ argc， argv， “{@input |莉娜.jpg |输入图像}” );

垫子图像 = imread（ samples：：findFile（ parser.get<String>（ “@input” ) ) );

如果（ 图像.empty（） ） ）

{

cout << "Could not open or find the image!\n" << endl;

cout << "Usage: " << argv[0] << " <Input image>" << endl;

return -1;

}

• Now, since we will make some transformations to this image, we need a new Mat object to store it. Also, we want this to have the following features:
  • Initial pixel values equal to zero
  • Same size and type as the original image

Mat new_image = Mat::zeros( image.size(), image.type() );

We observe that?cv::Mat::zeros?returns a Matlab-style zero initializer based on?image.size()?and?image.type()

• We ask now the values of?\alpha?and?\beta?to be entered by the user:αβ

double alpha = 1.0; /*< Simple contrast control */

int beta = 0;/*< 简单的亮度控制 */

cout << “基本线性变换” << endl;

cout << “-------------------------” << endl;

cout << “* 输入 alpha 值 [1.0-3.0]： ”;Cin >> Alpha;

cout << “* 输入 beta 值 [0-100]： ”;Cin >> β;

• 现在，要执行操作?g（i，j） = \alpha \cdot f（i，j） + \beta，我们将访问图像中的每个像素。由于我们使用的是 BGR 图像，因此我们将为每个像素（B、G 和 R）提供三个值，因此我们也将单独访问它们。这是一段代码：g(?i，j）=α?f(i，j)+β

for（ int y = 0; y <图像。行;y++ ） {

for（ int x = 0; x < image.cols; x++ ） {

for（ int c = 0; c < image.channels（）; c++ ） {

new_image.at<Vec3b>（y，x）[c] =

saturate_cast<uchar>（ alpha*image.at<Vec3b>（y，x）[c] + beta ）;

}

}

}

请注意以下内容（仅限 C++ 代码）：

• 为了访问图像中的每个像素，我们使用以下语法：image.at<Vec3b>（y，x）[c]，其中y是行，x是列，c是B，G或R（0,1或2）。
• 由于运算 \alpha \cdot p（i，j） + \beta?可以给出超出范围的值或不是整数（如果?\alpha?是浮点数），因此我们使用?cv：：saturate_cast?来确保值有效。α?p（i，j)+βα
• 最后，我们以通常的方式创建窗口并显示图像。

注意

与其使用?for?循环来访问每个像素，不如简单地使用以下命令：

其中?cv：：Mat：：convertTo?将有效地执行 *new_image = a*image + beta*。但是，我们想向您展示如何访问每个像素。无论如何，这两种方法都会给出相同的结果，但 convertTo 更优化并且工作速度更快。

结果

• 运行我们的代码并使用?\alpha = 2.2?和?\beta = 50α=2.2β=50
  $ ./BasicLinearTransforms lena.jpg

  基本线性变换

  -------------------------

  * 输入 alpha 值 [1.0-3.0]：2.2

  * 输入 beta 值 [0-100]：50

• 我们得到这个：

  

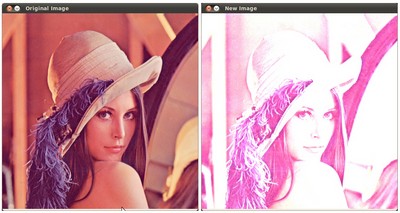
实例

在本段中，我们将通过调整图像的亮度和对比度来校正曝光不足的图像所学到的知识付诸实践。我们还将看到另一种校正图像亮度的技术，称为伽玛校正。

亮度和对比度调整

增加（/减少）\beta?值将为每个像素添加（/减去）一个常量值。超出 [0 ; 255] 范围的像素值将饱和（即高于（/小于）255 （/ 0） 的像素值将被限制为 255 （/ 0））。β

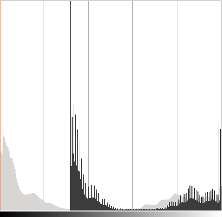
直方图表示每个颜色级别的像素数。深色图像将具有许多低色值的像素，因此直方图将在其左侧呈现峰值。当添加恒定偏差时，直方图会向右移动，因为我们为所有像素添加了恒定偏差。

\alpha?参数将修改级别的分布方式。如果?\alpha < 1?，则颜色级别将被压缩，结果将是对比度较低的图像。αα<1

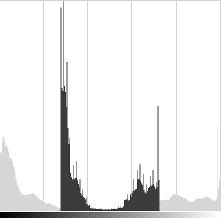
请注意，这些直方图是使用 Gimp 软件中的亮度对比度工具获得的。亮度工具应与 \beta?偏置参数相同，但对比度工具似乎与?\alpha?增益不同，其中输出范围似乎以 Gimp 为中心（如上一条直方图所示）。βα

可能会发生这样的情况：使用?\beta?偏差会提高亮度，但同时，由于对比度会降低，图像会出现轻微的面纱。\alpha?增益可用于减弱这种影响，但由于饱和，我们将丢失原始明亮区域中的一些细节。βα

伽玛校正

Gamma?校正可用于通过在输入值和映射输出值之间使用非线性变换来校正图像的亮度：

由于这种关系是非线性的，因此所有像素的效果都不相同，并且取决于它们的原始值。

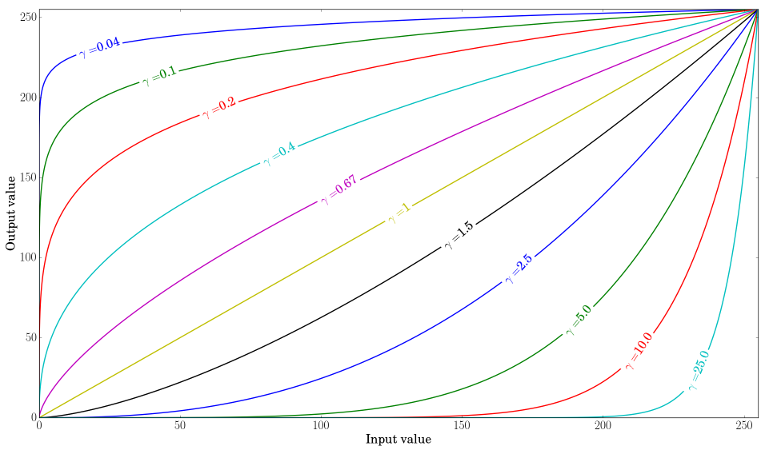
当?\gamma <?1 时，原始暗区会更亮，直方图会向右移动，而?\gamma > 1?则相反。γ<1γ>1

校正曝光不足的图像

下图已更正为：\?alpha = 1.3?和?\beta = 40。α=1.3β=40

整体亮度已得到改善，但您可以注意到，由于所用实现的数值饱和（摄影中的高光剪切），云层现在非常饱和。

下图已更正为：\?gamma = 0.4?。γ=0.4

伽马校正应该倾向于增加较少的饱和效应，因为映射是非线性的，并且不可能像以前的方法那样出现数值饱和。

上图比较了三个图像的直方图（三个直方图之间的 y 范围不同）。您可以注意到，大多数像素值都位于原始图像直方图的下部。在?\alpha?，?\beta?修正之后，由于饱和以及向右移动，我们可以观察到 255 处有一个大峰值。伽马校正后，直方图向右移动，但黑暗区域的像素比明亮区域的像素移动更多（参见伽马曲线图）。αβ

在本教程中，您已经了解了两种调整图像对比度和亮度的简单方法。它们是基本技术，不能用作光栅图形编辑器的替代品！

法典

C++爪哇岛蟒

伽玛校正代码：

查找表用于提高计算性能，因为只需计算一次 256 个值。