【模版】动态规划

背包问题

2. 01背包问题

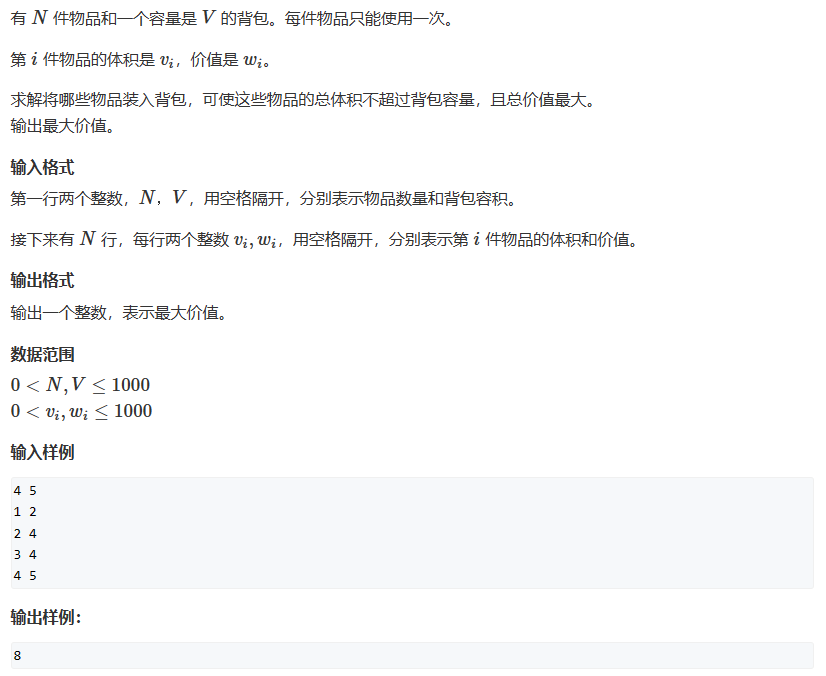
#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

int n, m;
int f[N][N];

int main() {
    
    cin >> n >> m;
    
    for (int i = 1; i <= n; i ++) {
        int v, w;
        cin >> w >> v;
        for (int j = 0; j <= m; j ++) {
            f[i][j] = f[i-1][j];
            if (j >= w) f[i][j] = max(f[i][j], f[i-1][j-w] + v);
        }
    }
    
    cout << f[n][m];
    
    
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int f[N];

int main() {

    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) {
        
        int v, w;
        
        cin >> v >> w;
        
        for (int j=m; j>=v; j-- ) {
            f[j] = max(f[j], f[j - v] + w);
        }
        
    }
    cout << f[m];
    return 0;
}

---

3. 完全背包问题

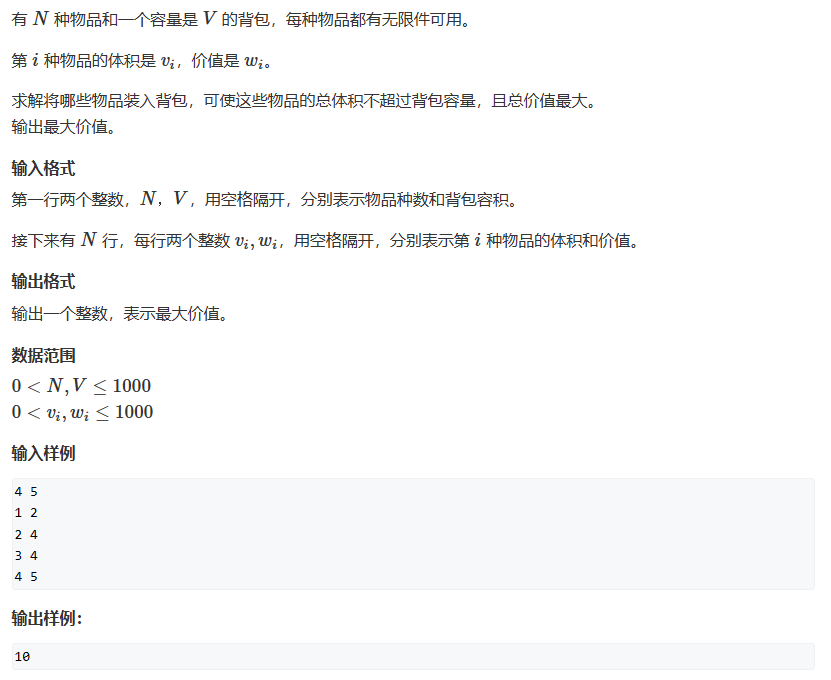
#include <bits/stdc++.h>
using namespace std;

const int N = 1001;

int f[N][N];

int n, m;

int main() {
    
    cin >> n >> m;
    
    for (int i = 1; i <= n; i ++ ) {
        int v, w;
        cin >> v >> w;
        
        for (int j = 0; j <= m; j ++ ) {
            f[i][j] = f[i - 1][j];
            if (j >= v) f[i][j] = max(f[i][j], f[i][j - v] + w);
        }
    }
    
    cout << f[n][m];
    
    return 0;
}

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

int n, m;

int f[N];

int main() {
    
    cin >> n >> m;
    
    for (int i = 0; i < n; i ++ ) {
        int v, w;
        cin >> v >> w;
        for (int j = v; j <= m; j ++ ) {
            f[j] = max(f[j], f[j - v] + w);
        }
    }
    
    cout << f[m];
    
    
    return 0;
    
}

---

4. 多重背包问题 I

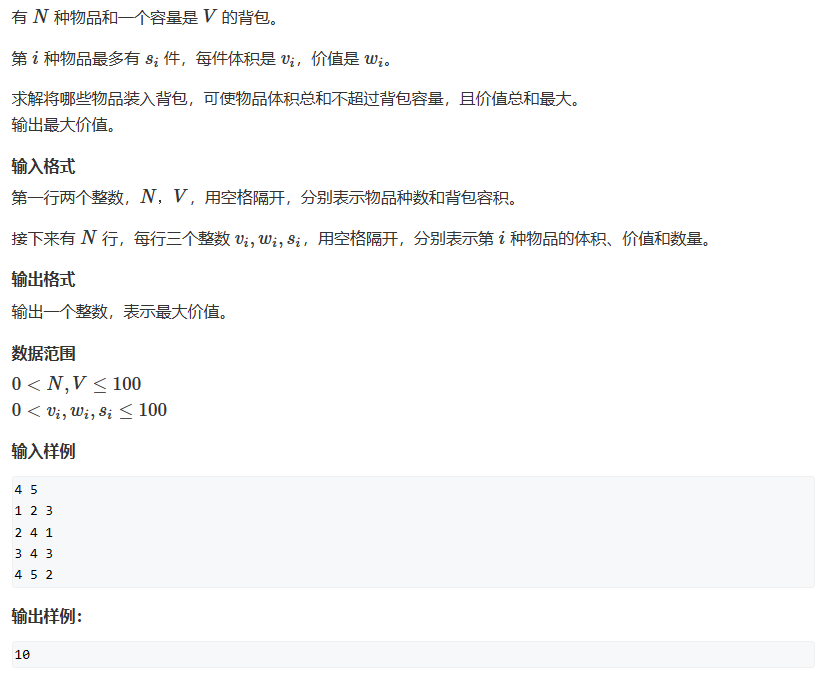
#include <bits/stdc++.h>
using namespace std;

const int N = 10010;
int n, m, s, v[N], w[N], cnt;
int f[N][110];

int main() {
    
    scanf("%d%d", &n, &m);
    
    for(int i=0; i<n; i++) {
        
        int a, b;
        scanf("%d%d%d", &a, &b, &s);
        while(s--) {
            v[++cnt] = a;
            w[cnt] = b;
        }
    }
    
    
    for(int i=1; i<=cnt; i++) {
        for(int j=1; j<=m; j++) {
            f[i][j] = f[i-1][j];
            if(j>=v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
        }
    }
    
    printf("%d", f[cnt][m]);
    
    return 0;
}

#include <bits/stdc++.h>
using namespace std;


const int N = 110;
typedef pair<int, int> PII;

int n, m;

vector<PII> G;

int f[N];

int main() {
    
    
    cin >> n >> m;
    
    for (int i = 0; i < n; i ++ ) {
        
        int v, w, s;
        cin >> v >> w >> s;
        
        for (int k = 1; k <= s; k *= 2) {
            s -= k;
            G.push_back({k * v, k * w});
        }
        
        if(s) G.push_back({s * v, s * w});
    }
    
    
    for (int i = 0; i < G.size(); i ++ ) {
        int v = G[i].first, w = G[i].second;
        for (int j = m; j >= v; j -- ) {
            f[j] = max(f[j], f[j - v] + w);
        }
    }
    
    
    cout << f[m];
    
    
    return 0;
}

---

5. 多重背包问题 II

#include <bits/stdc++.h>
using namespace std;

const int N = 2010;
typedef pair<int, int> PII;

int n, m;
int f[N];

vector<PII> G;

/*
    首先可以利用每个物品分成 s 份，跑 01 背包， 但是会超时
    进一步优化利用二进制来表示物品个数：
    例如： 14 ： 1 2 4 7   
           6  ： 1 2 3 
    可以看出最后一个特殊处理，不能超出所要表达的物品个数


*/


int main() {
    
    cin >> n >> m;
    
    for (int i = 1; i <= n; i ++ ) {
        int v, w, s;
        cin >> v >> w >> s;
        for (int k = 1; k <= s; k *= 2) {
            s -= k;
            G.push_back({k * v, k * w});
        }
        if (s > 0) G.push_back({s * v, s * w}); //把最后剩余的部分装入进去;
    }
    
    
    //利用上述就可以跑 01 背包模型啦
    
    for (int i = 0; i < G.size(); i ++ ) {
        int v = G[i].first, w = G[i].second;
        for (int j = m; j >= v; j -- ) {
            f[j] = max(f[j], f[j - v] + w);
        }
    }
    
    cout << f[m];
    
    
    return 0;
}

---

9. 分组背包问题

#include <bits/stdc++.h>
using namespace std;

const int N = 110;

int v[N][N], w[N][N], s[N];

int n, m;

int f[N][N];

int main() {
    
    cin >> n >> m;
    
    for (int i = 1; i <= n; i ++ ) {
        
        cin >> s[i];
        
        for (int j = 0; j < s[i]; j ++ ) {
            cin >> v[i][j] >> w[i][j];
        }
        
    }
    
    for (int i = 1; i <= n; i ++ ) {
        for (int j = 0; j <= m; j ++ ) {
            for (int k = 0; k <= s[i]; k ++ ) {
                if (v[i][k] <= j) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
            }
        }
    }
    
    cout << f[n][m];
    
    
    return 0;
}

---

线性DP

898. 数字三角形

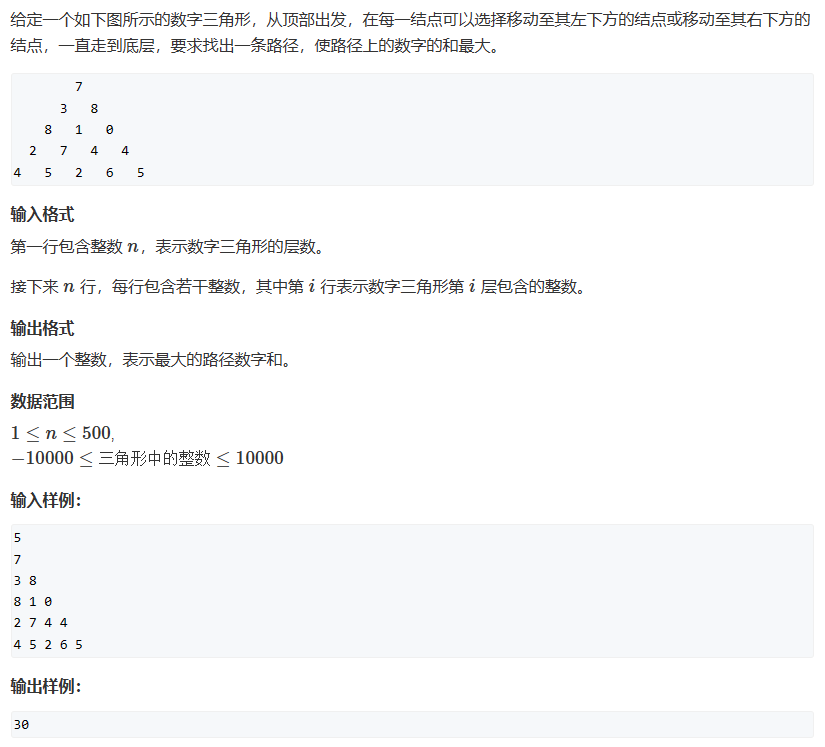
#include <bits/stdc++.h>
using namespace std;

const int N = 510;

int f[N][N], w[N][N];
int n;

int main() {
    
    cin >> n;
    
    for (int i = 1; i <= n; i ++ ) {
        for (int j = 1; j <= i; j ++ ) {
            cin >> w[i][j];
        }
    }
    
    memset(f, -0x3f, sizeof f);
    f[1][1] = w[1][1];
    for (int i = 2; i <= n; i ++ ) {
        for (int j = 1; j <= i; j ++ ) {
            f[i][j] = max(f[i - 1][j - 1] + w[i][j], f[i][j]);
            f[i][j] = max(f[i][j], f[i - 1][j] + w[i][j]);
        }
    }
    
    int res = -0x3f3f3f3f;
    
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
    
    
    cout << res;
    
    
    
    return 0;
}

---

895. 最长上升子序列

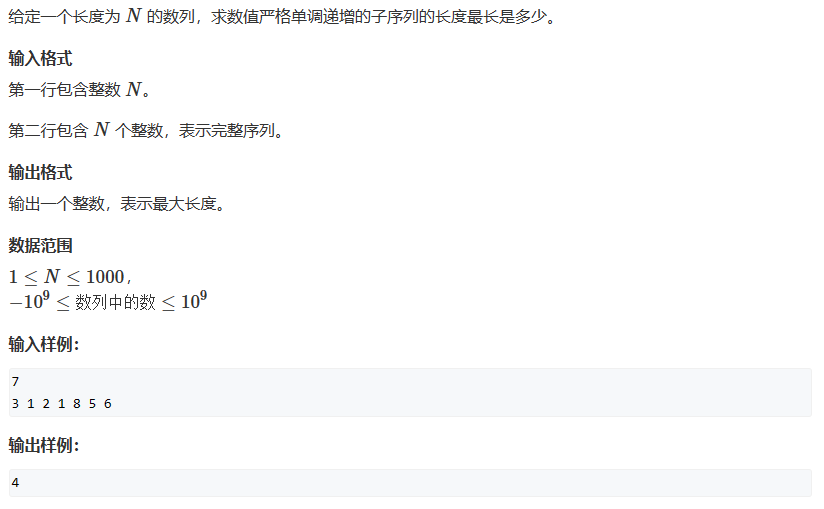
#include <bits/stdc++.h>
using namespace std;

int n;

const int N = 1010;

int f[N], a[N];

int main() {
    
    cin >> n;
    
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    
    for (int i = 1; i <= n; i ++ ) {
        f[i] = 1;
        for (int j = 1; j <= i; j ++ ) {
            if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
        }
    }
    
    int res = 0;
    
    for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);
    
    cout << res;
    
    
    return 0;
}

---

896. 最长上升子序列 II

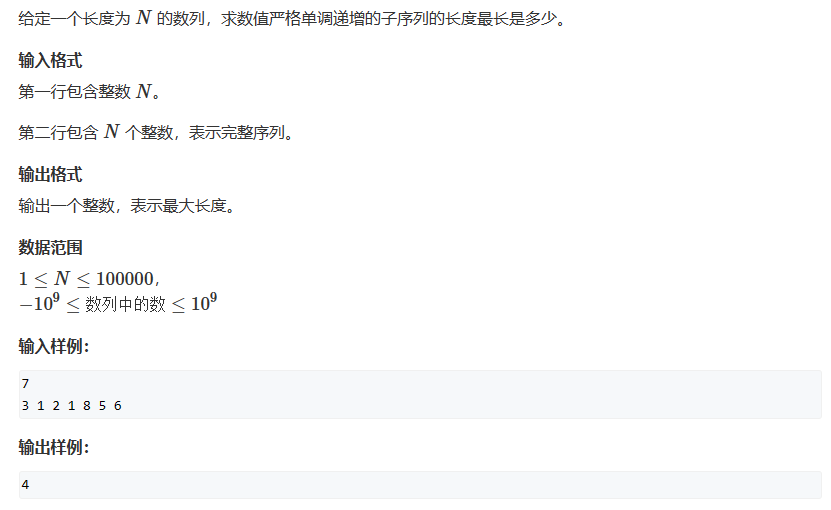
#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
vector<int> s;
int a[N];

int main() {
    int n;
    cin >> n;
    for(int i=1; i<=n; i++) {
        cin >> a[i];
    }
    
    s.push_back(a[1]);
    for(int i=2; i<=n; i++) {
        if(a[i] > s.back()) {
            s.push_back(a[i]);
        } else {
            *lower_bound(s.begin(), s.end(), a[i]) = a[i];
        }
    }
    
    cout << s.size();
    
    return 0;
}

---

897. 最长公共子序列

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

char a[N], b[N];
int n, m;
int f[N][N];

int main() {
    
    scanf("%d %d", &n, &m);
    scanf("%s %s", a+1, b+1);
    
    for (int i = 1; i <= n; i ++ ) {
        for (int j = 1; j <= m; j ++ ) {
            f[i][j] = max(f[i-1][j], f[i][j-1]);
            if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i-1][j-1] + 1);
        }
    }
    
    cout << f[n][m];
    
    return 0;
}

---

902. 最短编辑距离

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];

int main() {
    
    scanf("%d %s", &n, a + 1);
    scanf("%d %s", &m, b + 1);
    
    // memset (f, 0x3f, sizeof f);
    
    for (int i = 1; i <= n; i ++ ) f[i][0] = i;
    for (int i = 1; i <= m; i ++ ) f[0][i] = i;
    
    for (int i = 1; i <= n; i ++ ) {
        for (int j = 1; j <= m; j ++ ) {
            f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
            f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
        }
    }
    
    cout << f[n][m];
    
    return 0;
}

---

899. 编辑距离

---

区间DP

282. 石子合并

#include <bits/stdc++.h>
using namespace std;

const int N = 310;

int n;
int f[N][N], s[N];

int main() {
    
    cin >> n;
    
    for (int i = 1; i <= n; i ++ ) {
        cin >> s[i];
        s[i] += s[i - 1];
    }
    
    for (int len = 2; len <= n; len ++ ) {
        for (int l = 1; l + len - 1 <= n; l ++ ) {
            int r = l + len - 1;
            f[l][r] = 2e9;
            for (int k = l; k < r; k ++ ) {
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
            }
        }
    }
    
    cout << f[1][n];
    
    return 0;
}

---

计数类DP

900. 整数划分

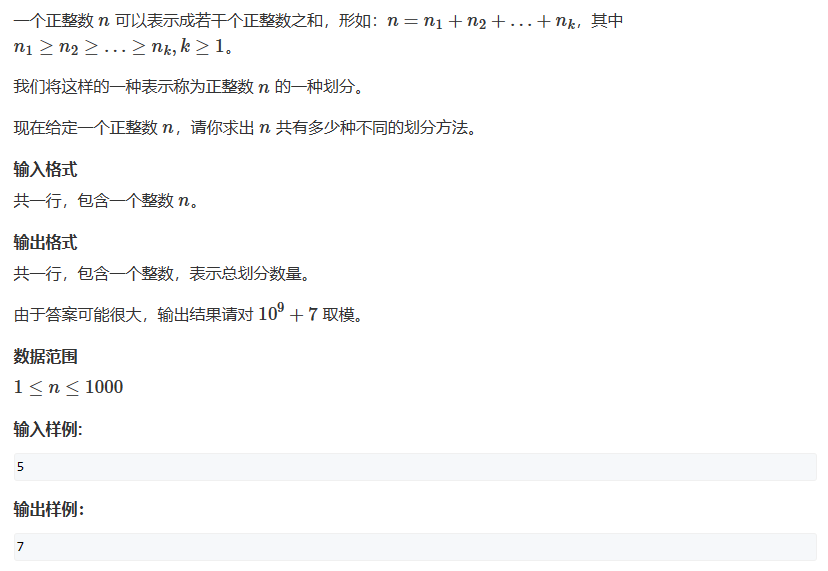
#include <bits/stdc++.h>
using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n;
int f[N][N];


int main() {
    
    cin >> n;
    
    f[1][1] = 1;
    
    for (int i = 2; i <= n; i ++ ) {
        for (int j = 1; j <= i; j ++ ) {
            f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
        }
    }
    
    int res = 0;
    
    for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;
    
    cout << res;
    
    return 0;
}

---

数位统计DP

338. 计数问题

---

状态压缩DP

291. 蒙德里安的梦想

#include <bits/stdc++.h>
using namespace std;

const int N = 12, M = 1 << N;
typedef long long LL;
bool st[M]; //存储所有的合法的偶数个数，奇数为false
vector<vector<int> > state(M); //存数所有合法的
LL f[N][M];
int n, m;

int main() {

    while(cin >> n >> m, n || m) {

        for(int i=0; i<1<<n; i++) {

            int cnt = 0;
            bool is_valid = true;
            for(int j=0; j<n; j++) {
                if(i>>j & 1) {
                    if(cnt & 1) {
                        is_valid = false;
                        break;
                    }
                } else {
                    cnt++;
                }
            }

            //处理最后一位
            if(cnt & 1) is_valid = false;
            st[i] = is_valid;
        }

        for(int i=0; i<1<<n; i++) {
            state[i].clear();
            for(int j=0; j<1<<n; j++) {
                //所有空余的列位置有偶数个,并且与偶数个0即st[i | j] 合法
                if((i & j)==0 && st[i | j])
                    state[i].push_back(j);
            }

        }


        memset(f, 0, sizeof f);
        //这里因为不可能有从第-1行伸到第0行，即为空棋盘的时候
        f[0][0] = 1;

        //处理到m列
        for(int i=1; i<=m; i++) {
            //对于每个棋盘遍历所有的合法状态
            for(int j=0; j<1<<n; j++) {
                for(auto k : state[j]) {
                    f[i][j] += f[i-1][k];
                }
            }
        }

        cout << f[m][0] << endl;

    }

    return 0;
}

---

91. 最短Hamilton路径

#include <bits/stdc++.h>
using namespace std;

const int N = 21, M = 1 << N;

int n;
int f[M][N];
int w[N][N];

int main() {
    
    cin >> n;
    
    for (int i = 0; i < n; i ++ ) 
        for (int j = 0; j < n; j ++ )  
            cin >> w[i][j];
            
    memset(f, 0x3f, sizeof f);
    
    
    /*
        f[state][j] = f[state_k][k] + w[k][j], 表示的是
        f[state][j] ： state的走法中走到的终点为 j 
        f[state_k][k] ： state 的上一个状态，即需要遍历所有情况来判断: 去掉 j 后其中所有走到 k 的走法，再从k 到 j 
    
    */
    
    f[1][0] = 0;
    for (int i = 0; i < 1 << n; i ++ ) {
        for (int j = 0; j < n; j ++ ) {
            if (i >> j & 1) {
                for (int k = 0; k < n; k ++ ) {
                    //i - (1 << j)表示不包含点 j, 终点为点 k 的最小值
                    if (i - (1 << j) >> k & 1) {
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
                    }
                }
            }
        }
    }
    
    cout << f[(1 << n) - 1][n - 1] << endl;
    
    return 0;
}

---

树形DP

285. 没有上司的舞会

#include <bits/stdc++.h>
using namespace std;

const int N = 6010;
int n, h[N];
bool st[N];
vector<int> G[N];
int f[N][2];

int dfs(int u) {
    
    f[u][1] = h[u];
    
    int res = 0;
    
    for(auto j : G[u]) {
        dfs(j);
        f[u][1] += f[j][0];
        f[u][0] += max(f[j][1], f[j][0]);
    }
    
    res = max(f[u][0], f[u][1]);
    
    return res;
}

int main() {
    
    scanf("%d", &n);
    
    for(int i=1; i<=n; i++) scanf("%d", &h[i]);
    
    for(int i=1; i<n; i++) {
        int a, b;
        scanf("%d%d", &a, &b);
        G[b].push_back(a);
        st[a] = true;
    }
    
    int root = 1;
    
    while(st[root]) root++;
    
    cout << dfs(root);
    
    return 0;
}

---

记忆化搜索

901. 滑雪

#include <bits/stdc++.h>
using namespace std;

const int N = 310;

int r, c;
int h[N][N], f[N][N];

int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};

int dp(int x, int y) {
    int &v= f[x][y];
    if(v) return v;
    v = 1;
    for(int i=0; i<4; i++) {
        int a = x + dx[i], b = y + dy[i];
        if(a>=1 && a<=r && b>=1 && b<=c && h[a][b]<h[x][y]) {
            //取四个方向中最大的那个
            v = max(v, dp(a, b) + 1);
        }
    }
    
    return v;
}

int main() {
    
    
    scanf("%d%d", &r, &c);
    
    for(int i=1; i<=r; i++) {
        for(int j=1; j<=c; j++) {
            scanf("%d", &h[i][j]);
        }
    }
    
    int res = 0;
    for(int i=1; i<=r; i++) {
        for(int j=1; j<=c; j++) {
            res = max(res, dp(i, j));
        }
    }
    
    cout << res;
    
    return 0;
}