简明FFT公式
1. 傅里叶变换
F ( ω ) = ∫ ? ∞ ∞ f ( x ) e ? i ω x d x F(\omega)=\int_{-\infty}^{\infty} f(x) e^{-i \omega x} d x F(ω)=∫?∞∞?f(x)e?iωxdx
2. 逆傅里叶变换
f ( x ) = 1 2 π ∫ ? ∞ ∞ F ( ω ) e i ω x d ω f(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega x} d \omega f(x)=2π1?∫?∞∞?F(ω)eiωxdω
f(x)是一个关于时间t的函数,信号处理中代表信号值
F(ω)为信号在频域中的表示,描述原始函数f(t)在各个频率ω上的成分或强度
eiωx/e-iωx是旋转因子
3. 离散傅里叶变换(DFT)
A k = ∑ n = 0 N ? 1 e ? i 2 π N k n a n A_k=\sum_{n=0}^{N-1} e^{-i \frac{2 \pi}{N} k n} a_n Ak?=n=0∑N?1?e?iN2π?knan?
傅里叶变换针对连续信号,离散傅里叶DFT针对采样得到的离散信号
an表示第n个采样点处(或者说在时间n)信号的强度
Ak表示该信号在频率k上的强度或振幅
总的来说,an是输入信号的离散时间域表示,经过DFT后,将这个时域的表示转换为频域的表示Ak
DFT通常写作:
A
k
=
∑
n
=
0
N
?
1
W
N
k
n
a
n
A_k=\sum_{n=0}^{N-1} W_N^{k n} a_n
Ak?=n=0∑N?1?WNkn?an?
其中,
W
N
=
e
?
i
2
π
N
W_N=e^{-i \frac{2 \pi}{N}}
WN?=e?iN2π?
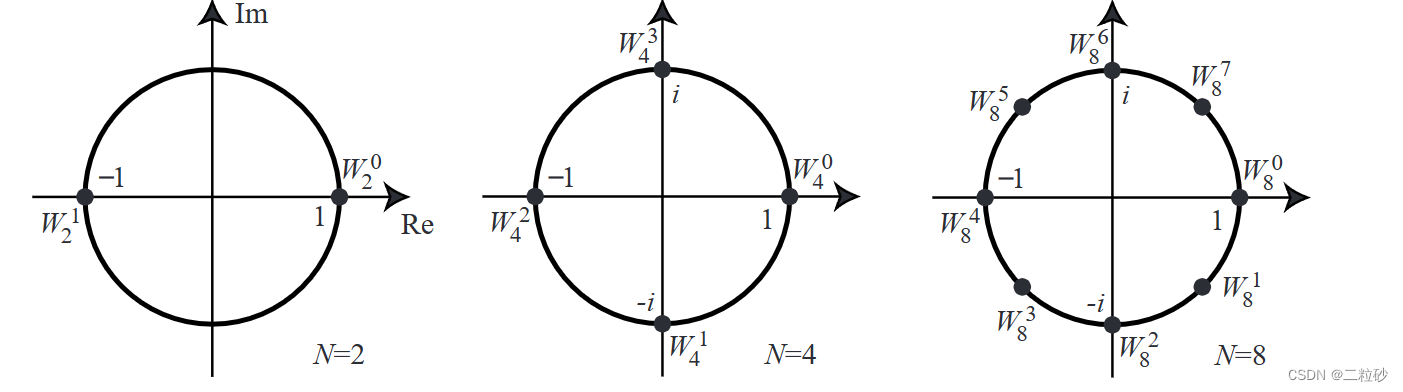
W N k W_N^k WNk? ( k = 0 … N ? 1 k=0 \ldots N-1 k=0…N?1) 通常被称为N次单位根。因为在复数运算中, ( W N k ) N = 1 \left(W_N^k\right)^N=1 (WNk?)N=1. 复平面上绘制的 N = 2 , N = 4 N=2, N=4 N=2,N=4, N = 8 N=8 N=8的单位根分别如下所示:
4. 逆离散傅里叶变换(IDFT)
a n = 1 N ∑ k = 0 N ? 1 W N ? k n A k a_n=\frac{1}{N}\sum_{k=0}^{N-1} W_N^{-k n} A_k an?=N1?k=0∑N?1?WN?kn?Ak?
其实就是换了个旋转因子
5. 快速傅里叶变换FFT
Cooley-Turkey算法是应用最广泛的FFT算法,采用分而治之的方法,将大DFT分解为小DFT,公式如下:
A k = ∑ n = 0 N ? 1 a n W N n k , k = 0 , 1 , ? ? , N ? 1 = ∑ n = 0 N / 2 ? 1 a 2 n W N 2 n k + ∑ n = 0 N / 2 ? 1 a 2 n + 1 W N ( 2 n + 1 ) k = ∑ n = 0 N / 2 ? 1 a 2 n W N 2 n k + W N k ∑ n = 0 N / 2 ? 1 a 2 n + 1 W N 2 n k = ∑ n = 0 N / 2 ? 1 a 2 n W N / 2 n k + W N k ∑ n = 0 N / 2 ? 1 a 2 n + 1 W N / 2 n k = F k + W N k G k , F k = ∑ n = 0 N / 2 ? 1 a 2 n W N / 2 n k , G k = ∑ n = 0 N / 2 ? 1 a 2 n + 1 W N / 2 n k , k = 0 , 1 , ? ? , N 2 ? 1 \begin{aligned} A_k & =\sum_{n=0}^{N-1}a_n W_N^{n k}, k=0,1, \cdots, N-1 \\ & =\sum_{n=0}^{N / 2-1} a_{2 n} W_N^{2 n k}+ \sum_{n=0}^{N / 2-1} a_{2 n+1} W_N^{(2 n+1) k} \\ & =\sum_{n=0}^{N / 2-1} a_{2 n} W_N^{2 n k}+W_N^k \sum_{n=0}^{N / 2-1} a_{2 n+1} W_N^{2 n k} \\ & =\sum_{n=0}^{N / 2-1} a_{2 n} W_{N / 2}^{n k}+W_N^k \sum_{n=0}^{N / 2-1} a_{2 n+1} W_{N / 2}^{n k} \\ & =F_k+W_N^k G_k, \\ F_k & =\sum_{n=0}^{N / 2-1} a_{2 n} W_{N / 2}^{n k}, G_k=\sum_{n=0}^{N / 2-1} a_{2 n+1} W_{N / 2}^{n k},k=0,1, \cdots, \frac N 2 -1 \end{aligned} Ak?Fk??=n=0∑N?1?an?WNnk?,k=0,1,?,N?1=n=0∑N/2?1?a2n?WN2nk?+n=0∑N/2?1?a2n+1?WN(2n+1)k?=n=0∑N/2?1?a2n?WN2nk?+WNk?n=0∑N/2?1?a2n+1?WN2nk?=n=0∑N/2?1?a2n?WN/2nk?+WNk?n=0∑N/2?1?a2n+1?WN/2nk?=Fk?+WNk?Gk?,=n=0∑N/2?1?a2n?WN/2nk?,Gk?=n=0∑N/2?1?a2n+1?WN/2nk?,k=0,1,?,2N??1?
由此将长度为N的DFT分解为两个长度为N/2的DFT,但是仅能得到前一半频率对应的结果
而由 W N / 2 n k = W N / 2 n ( k + N / 2 ) , W N n k = ? W N n ( k + N / 2 ) W_{N / 2}^{n k}=W_{N / 2}^{n (k+N/2)}, W_{N}^{n k}=-W_{N}^{n (k+N/2)} WN/2nk?=WN/2n(k+N/2)?,WNnk?=?WNn(k+N/2)?,可得 F k + N 2 = F k , G k + N 2 = G k F_{k+\frac N 2} = F_k, G_{k+\frac N 2} = G_k Fk+2N??=Fk?,Gk+2N??=Gk?,即:
A k + N 2 = F k + N 2 + W N k + N 2 G k + N 2 , k = 0 , 1 , ? ? , N 2 ? 1 = F k ? W N k G k \begin{aligned} A_{k+\frac N 2}& =F_{k+\frac N 2}+W_N^{k+\frac N 2} G_{k+\frac N 2},k=0,1, \cdots, \frac N 2 -1\\ &=F_k-W_N^k G_k \end{aligned} Ak+2N???=Fk+2N??+WNk+2N??Gk+2N??,k=0,1,?,2N??1=Fk??WNk?Gk??
DFT时间复杂度为 O ( N 2 ) {O}({N^2}) O(N2),FFT时间复杂度为 O ( N l o g 2 N ) O(Nlog_2N) O(Nlog2?N)
当FFT处理的离散序列长度为1,可以发现如下蝶形运算

蝶形运算组合成蝶形网络,以N=8的FFT为例:
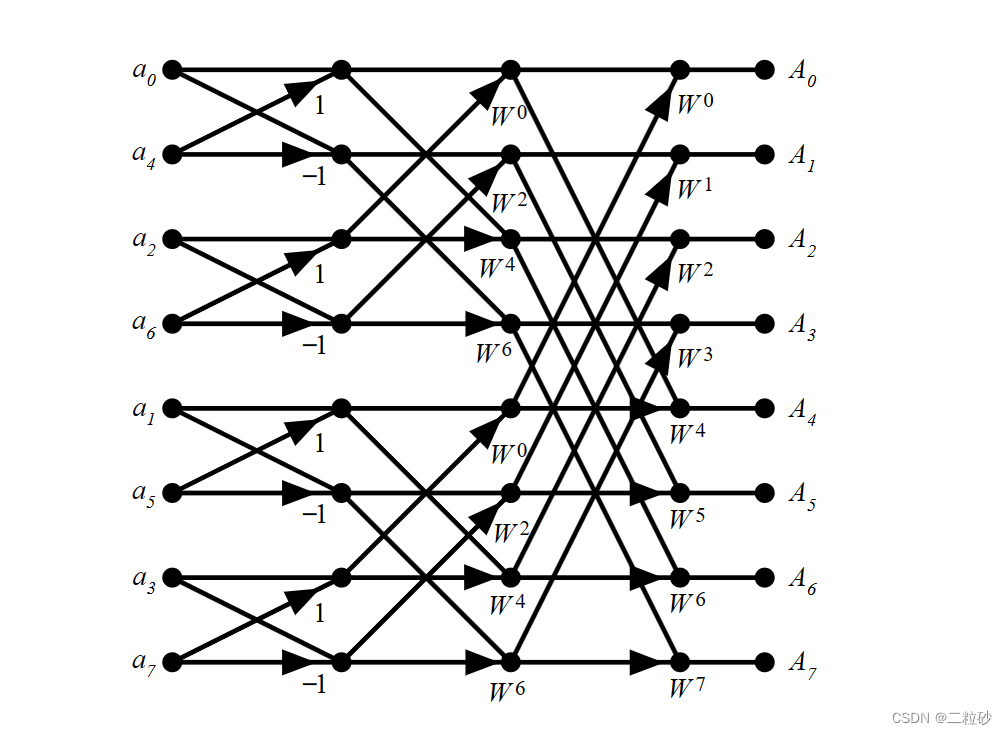
IFFT同理,换个旋转因子即可
———————————————————————————————— ———————————————————————————————— ————————————————————————————————
参考: Fourier transforms and the fast Fourier transform (FFT) algorithm
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 20240123-其实投资也不难
- 智能摄像机市场调研:应用行业范围已经达到了30%以上
- 第一章:简单句
- 纸箱回收投标书:可持续发展的生态环保解决方案
- 如何开发一个prompt?prompt的使用有哪些原则?
- JavaScript-sort()排序
- Linux Bridge 基本原理
- 【程序员英语】【美语从头学】初级篇(入门)(笔记)Lesson1-Lession5(打招呼、礼貌、姓名年龄和国籍、介绍、职业)
- 【无标题】Unlocking the Power of BMW ICOM Next: A Mini Guide
- SpringIOC之support模块DelegatingMessageSource