Answer on Mancherster MATH34001

2020Jan B6

WX:sobolev001

Question

(i) The parameter $\alpha$ is first considered to be real and in $(?1,1)$; define a branch for the function
$$f_6(z)=\frac{z^{\alpha }}{(z+1{)}^2}$$
and draw a clearly-labelled sketch of the complex $z$-plane showing the position of the branch cut and the only pole of this function. [2 marks]
(ii) State the formula for the residue of a pole of order $N$ at $z=z_0$ and use this formula to find the residue of $f_6(z)$ at its only pole. [5 marks]
(iii) By an integration of $f_6(z)$ around a suitable closed (keyhole) contour, show that, for $\alpha$ in the given range,
$$${\int }_0^{\infty }\frac{x^{\alpha }}{(x+1{)}^2}dx=\frac{\pi \alpha }{\sin (\pi \alpha )}.(?)$$ [8 marks]
(iv) Now consider $\alpha$ to be complex; use analytic continuation to show that $(?)$ holds in a certain domain $D$ (which you should find) of the complex $\alpha$-plane. [5 marks]

Ans:

(i) Choose the branch such that $0\le \text{arg}(z)<2\pi$. (i.e. the branch cut lies along the positive real axis See Fig. ).

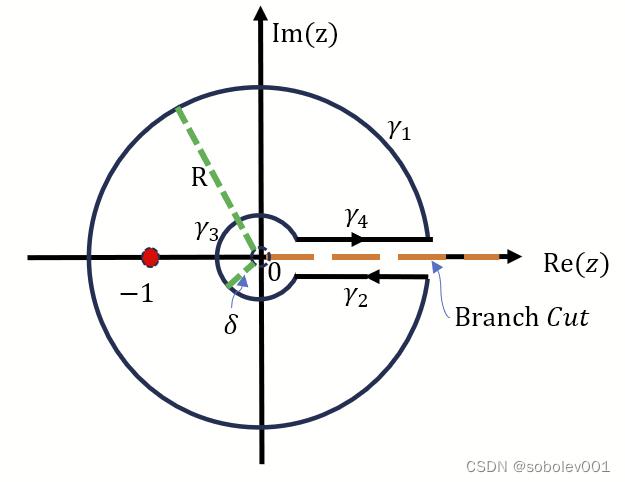
The only pole of $f_6(z)$ is $z_m=?1$ with order 2.

(ii) Def. The formula for the residue of a pole of order $N$ $$\mathrm{Res}(f;z_0)=\underset{z\to z_0}{\lim }\left(\frac{1}{(N?1)!}\frac{{\mathrm{d}}^{N?1}}{\mathrm{d}{z}^{N?1}}\left((z?z_0{)}^{N}f(z)\right)\right)$$
Hence, the residue of $f_6$ at $?1$ is
$$\mathrm{Res}(\frac{z^{\alpha }}{(z+1{)}^2};?1)=\underset{z\to ?1}{\lim }\left(\frac{1}{(2?1)!}\frac{{\mathrm{d}}^{2?1}}{\mathrm{d}{z}^{2?1}}\left((z+1{)}^2\frac{z^{\alpha }}{(z+1{)}^2}\right)\right)$$
$$=\underset{z\to ?1}{\lim }\left(\frac{\mathrm{d}}{\mathrm{d}z}\left(z^{\alpha }\right)\right)=\alpha (?1{)}^{\alpha ?1}=\alpha e^{i(\alpha ?1)\pi }$$
(iii) We will make use of a keyhole contour $C={\gamma }_1\cup {\gamma }_2\cup {\gamma }_3\cup {\gamma }_4$ (See Fig.)
a) For ${\gamma }_1$, we have
$$\left|{\int }_{{\gamma }_1}f(z)\mathrm{d}z\right|\le 2\pi R\underset{|z|=R}{\max }\left|\frac{z^{\alpha }}{(z+1{)}^2}\right|\le 2\pi R\frac{R^{\alpha }}{(R?1{)}^2}\to 0asR\to \infty .$$
b) For ${\gamma }_3$, we have
$$\left|{\int }_{{\gamma }_3}f(z)\mathrm{d}z\right|\le 2\pi \delta \underset{|z|=\delta }{\max }\left|\frac{z^{\alpha }}{(z+1{)}^2}\right|\le 2\pi \delta \frac{{\delta }^{\alpha }}{(1?\delta {)}^2}\to 0as\delta \to 0.$$
c) For ${\gamma }_2,{\gamma }_4$, we need the function values of $z^{\alpha }$ above and below the cut. So for $x>0$ we have
$$F_6(x+i0)=\frac{x^{\alpha }}{(x+1{)}^2},$$$$F_6(x?i0)=\frac{x^{\alpha }{e}^{i2\pi \alpha }}{(x+1{)}^2}.$$
Hence
$${\int }_{{\gamma }_4}{f}_6(z)\mathrm{d}z={\int }_{\delta }^R\frac{x^{\alpha }}{(x+1{)}^2}\mathrm{d}x$$
$${\int }_{{\gamma }_2}{f}_6(z)\mathrm{d}z={\int }_R^{\delta }\frac{x^{\alpha }{e}^{i2\pi \alpha }}{(x+1{)}^2}\mathrm{d}x=?{\int }_{\delta }^R\frac{x^{\alpha }{e}^{i2\pi \alpha }}{(x+1{)}^2}\mathrm{d}x$$
and so
$${\int }_{{\gamma }_2\cup {\gamma }_4}{f}_6(z)\mathrm{d}z=(1?e^{i2\alpha \pi }){\int }_{\delta }^R\frac{x^{\alpha }}{(x+1{)}^2}\mathrm{d}x$$
We therefore have
$${\int }_C{f}_6(z)\mathrm{d}z\to (1?e^{i2\alpha \pi }){\int }_0^{\infty }\frac{x^{\alpha }}{(x+1{)}^2}\mathrm{d}x$$
as $\delta \to 0,R\to \infty .$ Moreover, by Cauchy Residue Therom.
$${\oint }_{C}f(z)\mathrm{d}z=2i\pi \sum _{\stackrel{inside}{\mathrm{contourC}}}\mathrm{Residues}\mathrm{of}f(z)$$
Thus,
$$(1?e^{i2\alpha \pi }){\int }_0^{\infty }\frac{x^{\alpha }}{(x+1{)}^2}\mathrm{d}x=2\pi i?\alpha ?e^{i(\alpha ?1)\pi }$$
$${\int }_0^{\infty }\frac{x^{\alpha }}{(x+1{)}^2}\mathrm{d}x=\frac{2\pi i?\alpha ?e^{i(\alpha ?1)\pi }}{(1?e^{i2\alpha \pi })}=\frac{2\pi i?\alpha ?e^{i\alpha \pi }{e}^{?i\pi }}{(1?e^{i2\alpha \pi })}$$
$$=\frac{2\pi i?\alpha ?e^{i\alpha \pi }}{(e^{i2\alpha \pi }?1)}=\frac{2\pi i\alpha }{(e^{i\alpha \pi }?e^{?i\alpha \pi })}=\frac{\pi \alpha }{\sin (\pi \alpha )}$$