【现代控制理论笔记】——第六章:状态观测器
现代控制理论
第六章
1. 状态观测器简介
前述状态反馈配置极点的优越性,具有一个前提是状态全部是可以测量的,但实际并非如此,我们需要对系统状态进行重构,即观测器设计问题。
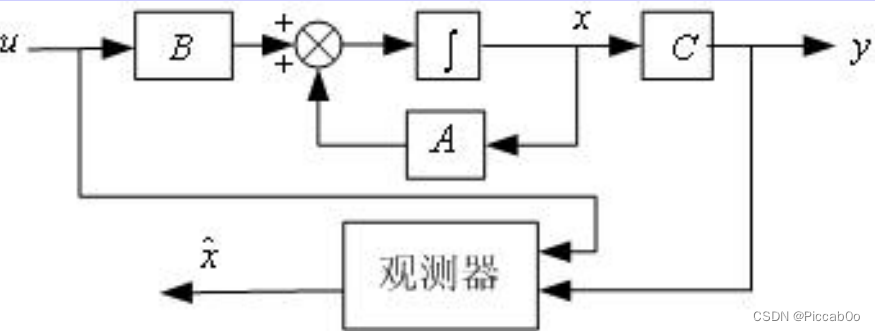
其原理是:
重新设计一个系统,用原系统的输入、输出作为它的输入信号,使其输出信号 x ^ \hat x x^等价于原系统的状态 x x x。
表述成:
z ˙ = F z + G y + H u , x ^ = M z + N y , \begin{aligned}\dot{z}&=Fz+Gy+Hu,\\\hat{x}&=Mz+Ny,\end{aligned} z˙x^?=Fz+Gy+Hu,=Mz+Ny,?
一般,如果观测器输出等价于原系统状态 x x x的称为状态观测器;输出等价于原系统状态函数 K x Kx Kx的称为函数观测器。
2. 全维状态观测器
状态维数等于原系统维数的观测器。
对于系统:
x ˙ = A x + B u y = C x \begin{aligned}\dot{x}&=Ax+Bu\\y&=Cx\end{aligned} x˙y?=Ax+Bu=Cx?
假设观测器的形式为:
z ˙ = F z + G y + H u x ^ = z \dot z = Fz+Gy+Hu\\ \hat x=z z˙=Fz+Gy+Hux^=z
则系统观测器的目标为:
l i m t → ∞ ( z ( t ) ? x ( t ) ) = 0 lim_{t\to\infty}(z(t)-x(t))=0 limt→∞?(z(t)?x(t))=0
可以看出,如果做差:
( z ˙ ? x ˙ ) = F z + G y + H u ? A x ? B u = F ( z ? x ) + ( F + G C ? A ) x + ( H ? B ) u . \begin{aligned} (\dot{z}-\dot{x})=& \begin{aligned}Fz+Gy+Hu-Ax-Bu\end{aligned} \\ =& F(z-x)+(F+GC-A)x+(H-B)u. \end{aligned} (z˙?x˙)==?Fz+Gy+Hu?Ax?Bu?F(z?x)+(F+GC?A)x+(H?B)u.?
且有 H = B H=B H=B, F = A ? G C F=A-GC F=A?GC, R e λ i ( F ) < 0 Re\lambda_i(F)<0 Reλi?(F)<0,则:
z ( t ) ? x ( t ) = e F t ( z ( 0 ) ? x ( 0 ) ) z(t)-x(t)=e^{Ft}(z(0)-x(0)) z(t)?x(t)=eFt(z(0)?x(0))
观测器目标成立,也就是需要:
A-GC的特征值具有具有负实部
此时全维状态观测器表示为:
z ˙ = ( A ? G C ) z + G y + B u \dot z = (A-GC)z+Gy+Bu z˙=(A?GC)z+Gy+Bu
基于前述状态反馈内容可知,若 ( A , C ) (A,C) (A,C)能观,则一定存在 G G G使极点可以任意配置(设计观测器也就是设计G),但反过来不一定成立。这里引入:

利用对偶性原理:

( A , B ) (A,B) (A,B)能稳充要条件是: r a n k [ s I ? A , B ] = n rank[sI-A,B]=n rank[sI?A,B]=n
进一步可知:

同时,对于状态观测器的形式有:

全维状态观测器的框图:
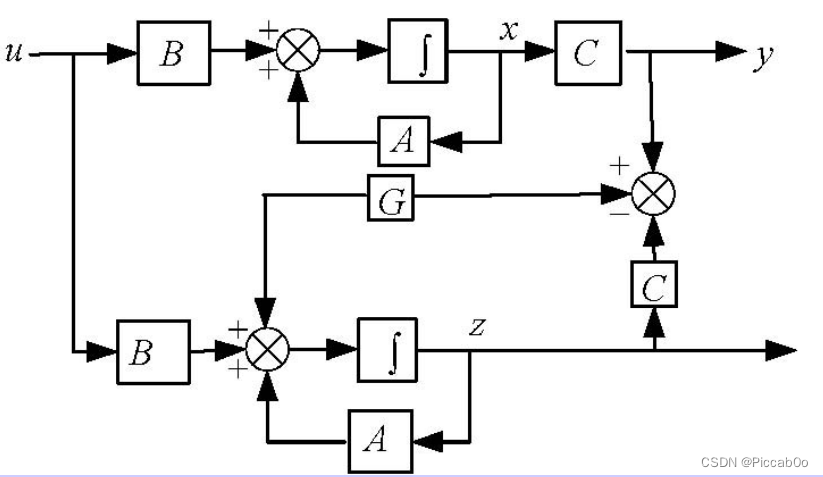
3. 基于全维状态观测器的输出动态反馈
对于系统:
x ˙ = A x + B u y = C x \dot x = Ax+Bu\\y=Cx x˙=Ax+Buy=Cx
引入全维状态观测器:
z ˙ = ( A ? G C ) z + G y + B u \dot z = (A-GC)z+Gy+Bu z˙=(A?GC)z+Gy+Bu
如果用观测状态 z z z作为状态反馈的状态,引入状态反馈:
u = K z + v u=Kz+v u=Kz+v
原系统变成了:
[ x ˙ z ˙ ] = [ A B K G C A ? G C + B K ] [ x z ] + [ B B ] ν y = [ C 0 ] [ x z ] \begin{aligned} \begin{bmatrix}\dot{x}\\\dot{z}\end{bmatrix}& =\begin{bmatrix}A&BK\\GC&A-GC+BK\end{bmatrix}\begin{bmatrix}x\\z\end{bmatrix}+\begin{bmatrix}B\\B\end{bmatrix}\nu \\ \text{y}& =\begin{bmatrix}C&0\end{bmatrix}\begin{bmatrix}x\\z\end{bmatrix} \end{aligned} [x˙z˙?]y?=[AGC?BKA?GC+BK?][xz?]+[BB?]ν=[C?0?][xz?]?
显然我们可以看出,状态观测器的引入改变了系统的维数为2n维,系统的特征值发生了变化:

但引入直接状态反馈后系统的闭环传递函数不因状态观测器的引入而改变。
说明:
可以看出,状态反馈和状态观测器的引入不互相影响对方已经配置好的特征值。这意味着:对于基于全维状态观测器的输出动态反馈系统,状态反馈控制律的设计和观测器的设计可独立地分开进行。
例题:

4. 降维状态观测器
考虑到系统输出中已经含有部分状态信息,可以用这部分信息构造一个维数低于系统维数的降维观测器。为此,设计观测器时对C进行分类讨论:
4.1 C = [ I q , 0 ] C=[I_q,0] C=[Iq?,0]时
考虑线性系统:
x ˙ = A x + B u y = [ I q 0 ] x \begin{aligned}\dot{x}&=Ax+Bu\\y&=\begin{bmatrix}I_q&0\end{bmatrix}x\end{aligned} x˙y?=Ax+Bu=[Iq??0?]x?
其n-q维状态观测器为:
ω ˙ = ( A 22 ? G A 12 ) ω + [ ( A 22 ? G A 12 ) G + ( A 21 ? G A 11 ) ] \dot\omega=(A_{22}-GA_{12})\omega+[(A_{22}-GA_{12})G+(A_{21}-GA_{11})] ω˙=(A22??GA12?)ω+[(A22??GA12?)G+(A21??GA11?)]
+ ( B 2 ? G B 1 ) u +(B_2-GB_1)u +(B2??GB1?)u
x ^ = [ y ω + G y ] \hat{x}=\begin{bmatrix}y\\\omega+Gy\end{bmatrix} x^=[yω+Gy?]
基于降维状态观测器的输出动态反馈
类似于全维状态观测器,降维观测器的引入也不改变系统的传递函数。
说明:

例题:

4.2 C行满秩时:
当C行满秩时,可以有非奇异线性变换:
T ? 1 = [ C ; R ] T^{-1}=[C;R] T?1=[C;R]
由 T ? 1 T = I n = [ C T ; R T ] T^{-1}T=I_n=[CT;RT] T?1T=In?=[CT;RT]得:
C T = I q = C ˉ CT=I_q=\bar C CT=Iq?=Cˉ
将原系统转化成 C = [ I q , 0 ] C=[I_q,0] C=[Iq?,0]的形式,原系统变换后:
A ˉ = T ? 1 A T = [ A 11 A 12 A 21 A 22 ] B ˉ = T ? 1 B = [ B 1 B 2 ] x ˉ = [ x 1 x 2 ] \begin{aligned}\bar{A}&=T^{-1}AT=\begin{bmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{bmatrix}\\\bar{B}&=T^{-1}B=\begin{bmatrix}B_1\\B_2\end{bmatrix}\\\bar{x}&=\begin{bmatrix}x_1\\x_2\end{bmatrix}\end{aligned} AˉBˉxˉ?=T?1AT=[A11?A21??A12?A22??]=T?1B=[B1?B2??]=[x1?x2??]?
待估计状态变成:
x ^ = T [ y ; w + G y ] \hat x = T[y;w+Gy] x^=T[y;w+Gy]
4.3 C行降秩的情况
当 r a n k C = m < q rankC=m<q rankC=m<q时,可以对C进行满秩分解:
C = E F C=EF C=EF
将系统改写成:
x ˙ = A x + B u y ~ = F x \begin{aligned}\dot{x}&=Ax+Bu\\\tilde{y}&=Fx\end{aligned} x˙y~??=Ax+Bu=Fx?
y ~ = ( E T E ) ? 1 E T y \tilde{y}=(E^TE)^{-1}E^Ty y~?=(ETE)?1ETy
用行满秩的情况进行分析。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 管理团队的5个策略和技巧,让你的团队更高效
- linux 完全卸载docker
- 为什么在开关电源待机工作不接负载的时候还是会产生EMC电磁干扰
- KBL410-ASEMI适配高端电源KBL410
- Python将txt转化为csv文件的pandas方法
- Linux入门攻坚——13、实战软件安装-搭建Python3.8环境-1
- 【大模型应用】小白借助chatgpt开发谷歌插件
- 【工具】推荐一个好用的代码画图工具
- 前端开发 3: JavaScript
- 嵌入式-C语言-江科大-数据类型&宏定义#define&关键字typedef&结构体