前端算法之二叉树
二叉树
二叉树是一种常见的树状数据结构,它由节点组成,每个节点最多有两个子节点:
- 左子节点
- 右子节点
这两个子节点可以为空,也可以连接到其他节点。二叉树具有以下特点:
- 每个节点最多有两个子节点。
- 左子节点在父节点的左边,右子节点在父节点的右边。
- 子节点可以为空。
下面是一个简单的二叉树例子:
1
/ \
2 3
/ \ / \
4 5 6 7
在这个例子中,数字表示节点的值,箭头表示子节点的连接关系。
根节点是1,它的左子节点是2,右子节点是3。节点2的左子节点是4,右子节点是5。节点3的左子节点是6,右子节点是7。
这就是一个二叉树的示例,每个节点最多有两个子节点,符合二叉树的定义。
更多详细内容,请微信搜索“前端爱好者“, 戳我 查看 。
前端设计的是遍历问题,例如:任意两个节点的最小的祖先
二叉树用于解决什么问题
二叉树是一种数据结构,它由节点组成,每个节点最多有两个子节点:左子节点和右子节点。这种数据结构通常用于解决各种问题,其中包括但不限于:
数据的组织与搜索:
二叉搜索树 (BST) 是一种常见的二叉树,它可以快速进行搜索、插入和删除操作。通过比较节点的值,可以有效地定位数据项,这在数据库索引和搜索引擎等领域很有用。
举例:在一个包含许多单词的二叉搜索树中搜索一个特定的单词,可以快速定位到该单词并提供相关信息。
排序:
二叉树可以用于排序算法中。比如,通过构建二叉搜索树并进行中序遍历,可以获得有序的数据。
举例:对一组数字进行排序,将它们构建成二叉搜索树,然后进行中序遍历,即可得到有序的数字序列。
表达式和计算:
表达式树是一种二叉树,用于表示数学表达式。它可以帮助进行表达式求值和运算。
举例:将数学表达式如"(3 + 4) * 5"表示成对应的二叉树结构,便于进行运算和求值。
图形处理:
在计算机图形学中,二叉树结构可以用来表示场景图或层次结构,例如场景中的物体组织结构。
举例:用二叉树表示一个计算机游戏中的场景,每个节点代表一个物体或者一个场景元素,并用树的结构表示它们之间的层次关系。
这些只是二叉树应用的一部分,它们在各种领域都有广泛的应用。
举例:二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
leetcode地址:https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/
最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
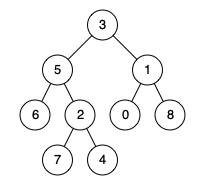
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。
思路: 排序/排布方式 和 (排序中)当前树和节点的关系
- 都位于左侧

- 位于两测

递归:
返回当前子树中,p和q 的最近祖先,没有,返回null
1. 当前遍历到p或者 q.不无要往下遍历,返回当前p q
2. 遍历到null,没有p q,返回nul
3. 遍历子树,左子树 右子树 都有结果,返回root
4. 只有其中一个子树有结果 p / q 只在这个子树下返回 null,null
结果:
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function(root, p, q) {
if(root == null){
return null
}
// 遇到p,遇到q,直接返回当前的节点
if(root ==p || root == q){
return root
}
// 递归操作
const left = lowestCommonAncestor(root.left, p, q)
const right = lowestCommonAncestor(root.right, p, q)
// 如果左子树和右子树都有节点,则返回root
if(left && right) {
return root
}
// 如果左节点没有,则返回右侧子树
if(!left){
return right
}
// 如果右节点没有,则返回左侧子树
if(!right){
return left
}
};
举例2:二叉搜索树的最近公共祖先
leetcode地址:https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/description/
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
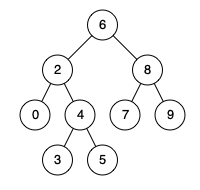
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
解答
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function(root, p, q) {
if(root == null){
return null
}
// 遇到p,遇到q,直接返回当前的节点
if(root ==p || root == q){
return root
}
// 递归操作
const left = lowestCommonAncestor(root.left, p, q)
const right = lowestCommonAncestor(root.right, p, q)
// 如果左子树和右子树都有节点,则返回root
if(left && right) {
return root
}
// 如果左节点没有,则返回右侧子树
if(!left){
return right
}
// 如果右节点没有,则返回左侧子树
if(!right){
return left
}
};
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【linux系统详细介绍】
- 漏刻有时数据可视化Echarts组件开发(45)机场流程导航线和指示点的开发记录
- Seer*Stat乳腺癌数据预测模型-Step3特征选择
- 什么情况?DDD 中的每个任务都执行了两次?
- 科技助力“双碳”:墨水屏电子桌牌在绿色办公中的作用
- discuz论坛附件上传限制大小2MB
- [前端已死论]——“Java 已死、前端已凉”
- 程序员裁员潮:技术变革下的职业危机
- word中在当前列表的基础上修改列表
- 双非本科准备秋招(5)——力扣回溯法解决链表问题、Collection接口的实现类与源码追踪1