【同济子豪兄斯坦福CS224W中文精讲】PageRank算法

发布时间：2024年01月12日

文章目录


互联网的图表示
网页是节点，网页之间的连接是边（这是二三十年前的互联网图表示
现在的互联网更加复杂的点在于首先网页本身是动态生成的、存在私域的爬虫不可触达的网页内容、网页之间的关系变得复杂是交互式的而非之前单一的导航式

有向图：若网页A中包含网页C的链接，则在node A到node C之间有一条有向边
使用连接信息来定量地计算节点重要度

三个PageRank变种算法
PageRank算法——节点重要度
Personlized Page Rank算法——节点相似度
Random Walk with Restarts算法——节点相似度
第一个算法用在搜索引擎、第二三个用在推荐系统

把link视为votes 考虑in-coming links，来自重要link的引用带来更大的vote

理解PageRank的五个角度

迭代求解线性方程组

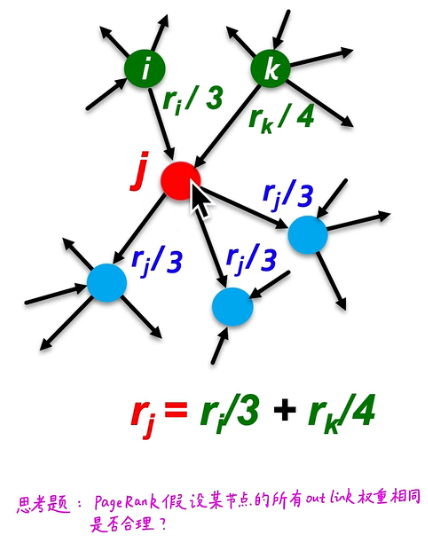
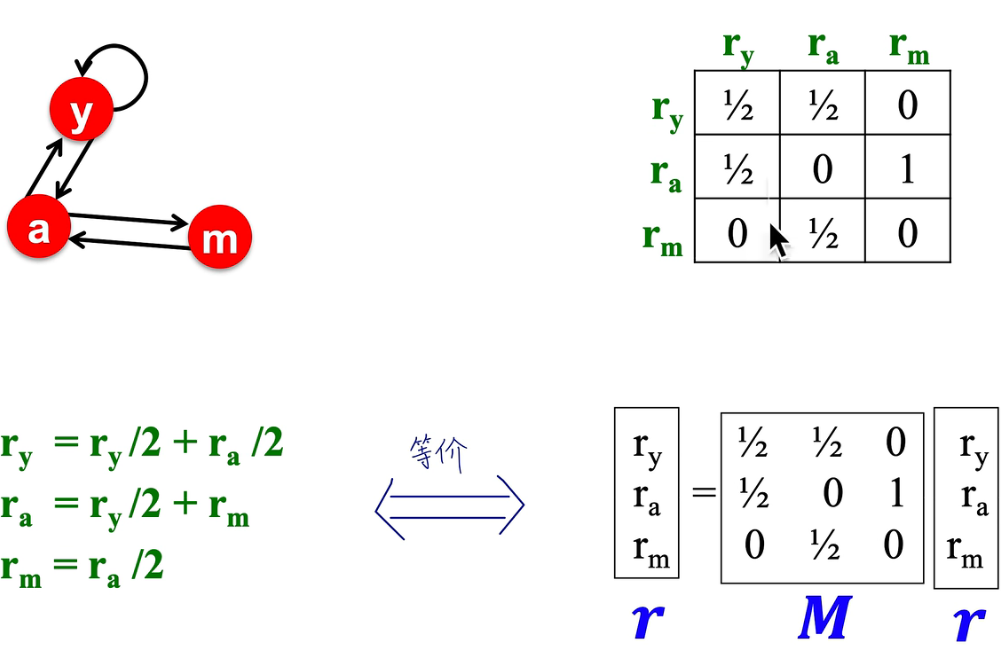
image.png

每个节点为其引用的节点提供vote值，提供的大小为该节点vote值/总引用node 数目

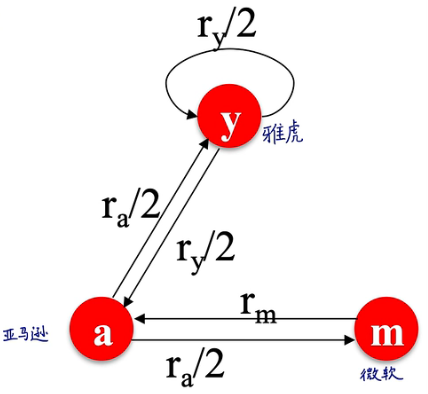
举个计算的例子：这里使用的高斯消元法，仅仅适合节点个数少，连接不复杂的情况，不能推广到像互联网网页连接那样的复杂网络中进行计算

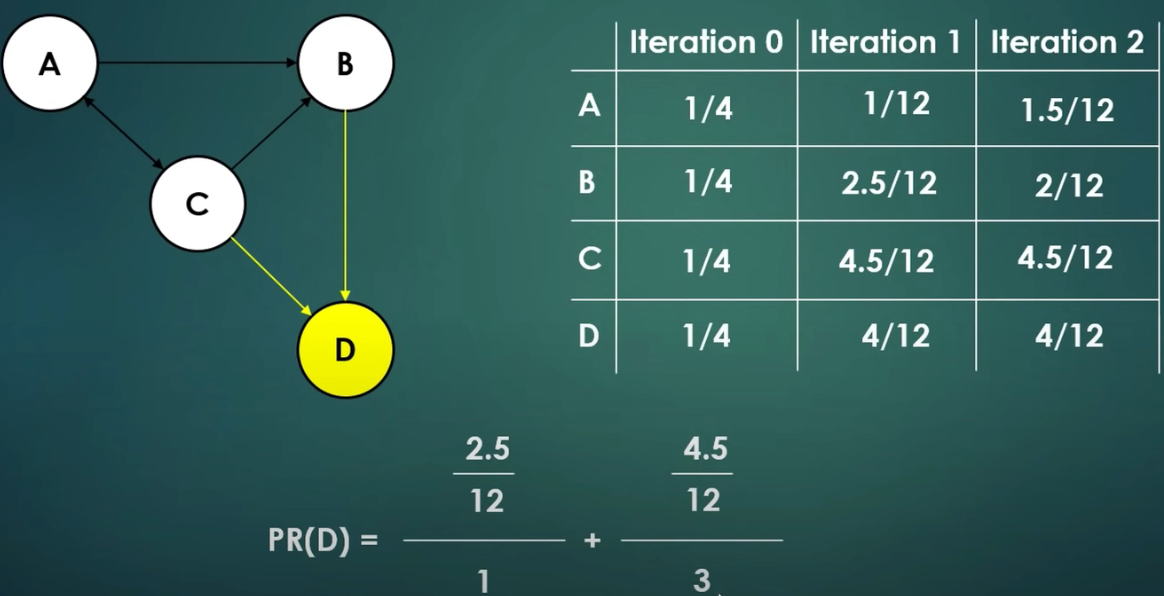
image.png
image.png

迭代计算示例：初始给所有节点分配相同的vote值，然后进行迭代直到各个节点vote值不再变化？
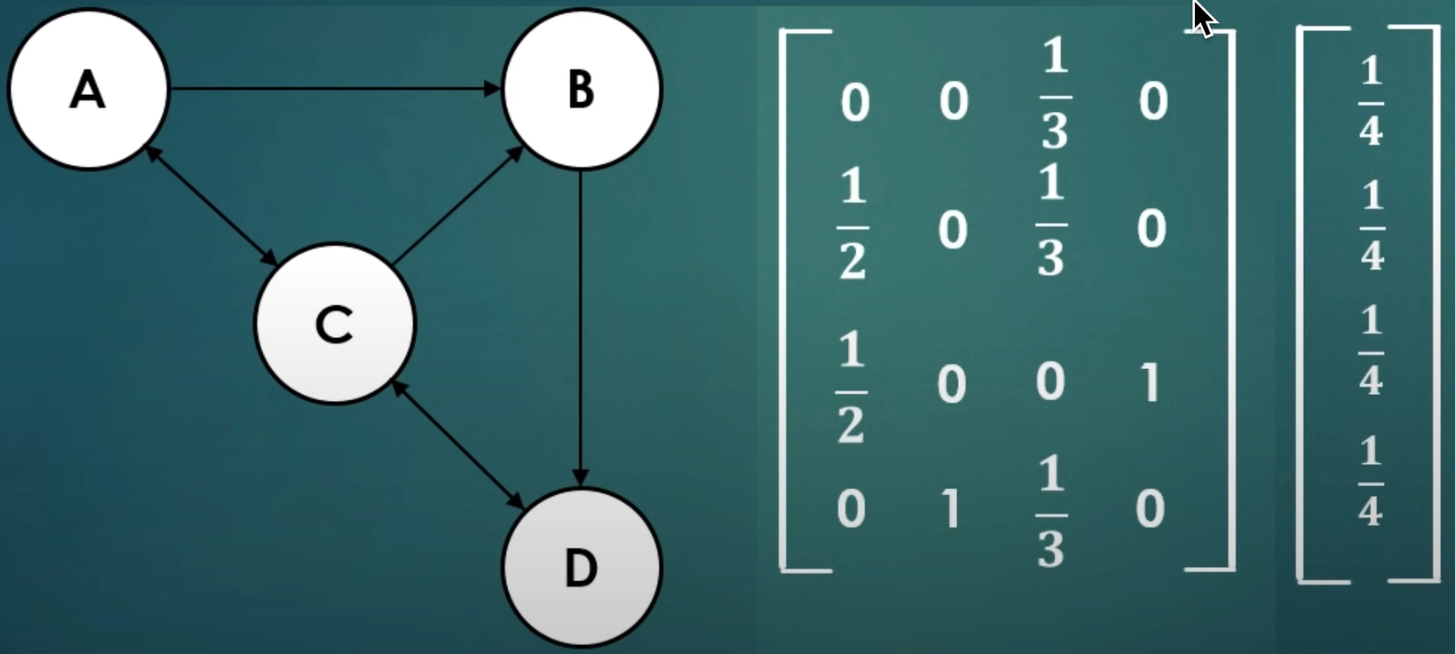
image.png

迭代左乘M矩阵

image.png

说明：仅适合静态的图，因为M矩阵无变化
r r r的每一个分量代表节点vote值，与M矩阵各行向量对应，行向量的各个分量即是 r r r中对应节点对该行代表节点的贡献权重。

M矩阵称为Stochastic adjacency matrix 概率邻接矩阵，每一列都是概率，每一列求和为1
r r r为pagerank向量， r i r_i ri?为page i的pagerank得分，n个节点对应 r r r为n维向量， ∑ i r i = 1 \sum_i r_i = 1 ∑i?ri?=1
r = M ? r r = M \cdot r r=M?r
线性方程组和矩阵点乘的对应：

image.png

矩阵的特征向量

根据左乘stochastic矩阵方法的flow equation，对于任何一个向量 u u u，经过 M ( M ( . . . M ( M u ) ) ) M(M(...M(Mu))) M(M(...M(Mu)))这样一个长期游走过程，最终收敛得到 r l e f t = r r i g h t r_{left}=r_{right} rleft?=rright?时， r r r为 M M M的主特征向量（特征值为1）
因而我们解决pagerank问题即是要找到stochastic adjacency matrix的主特征向量
这样一个方法被称为Power iteration即幂迭代过程

从数学的角度定理支撑其有解性：
image.png

随机游走

一个小人在这个网络中随机走动（按照有向图中的连接），走到一个节点，就增加其vote值，最终将所有节点的vote值归一化，得到pagerank分数
将这个过程总结为：随机游走、计数求和、归一化为概率，得到的就是pagerank分数值

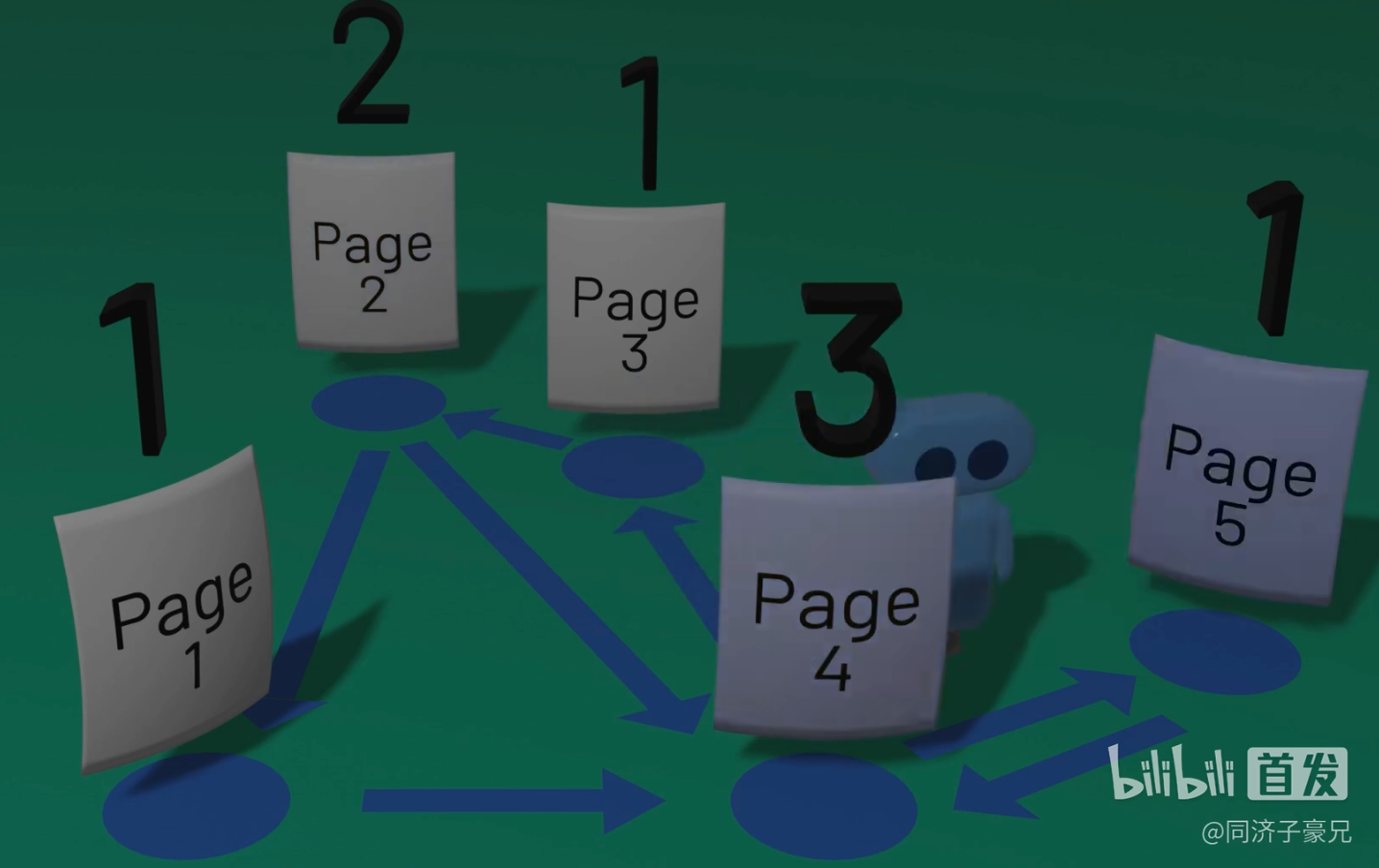
image.png

说明：我们在网络中假设一个surfer，在t时刻，surfer在节点i处，则在t+1时刻，surfer的位置应该是按照节点i的out-link随机到下一个节点j
于是，我们可以说这中情景下的pagerank值是等价于surfer在最终时刻也即稳定时它分布在各个节点处的概率。所有节点的分布概率值加和为1
p ( t + 1 ) = M ? p ( t ) p(t+1) = M \cdot p(t) p(t+1)=M?p(t)

马尔可夫链

状态和状态之间的转移信息来表示，图中节点表示状态，节点之间的连接表示状态的转移

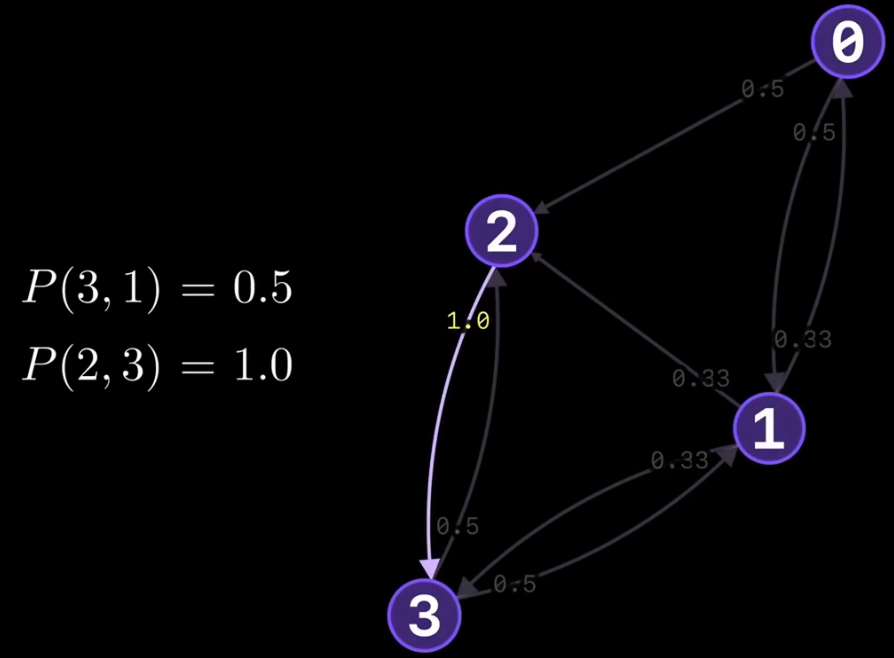
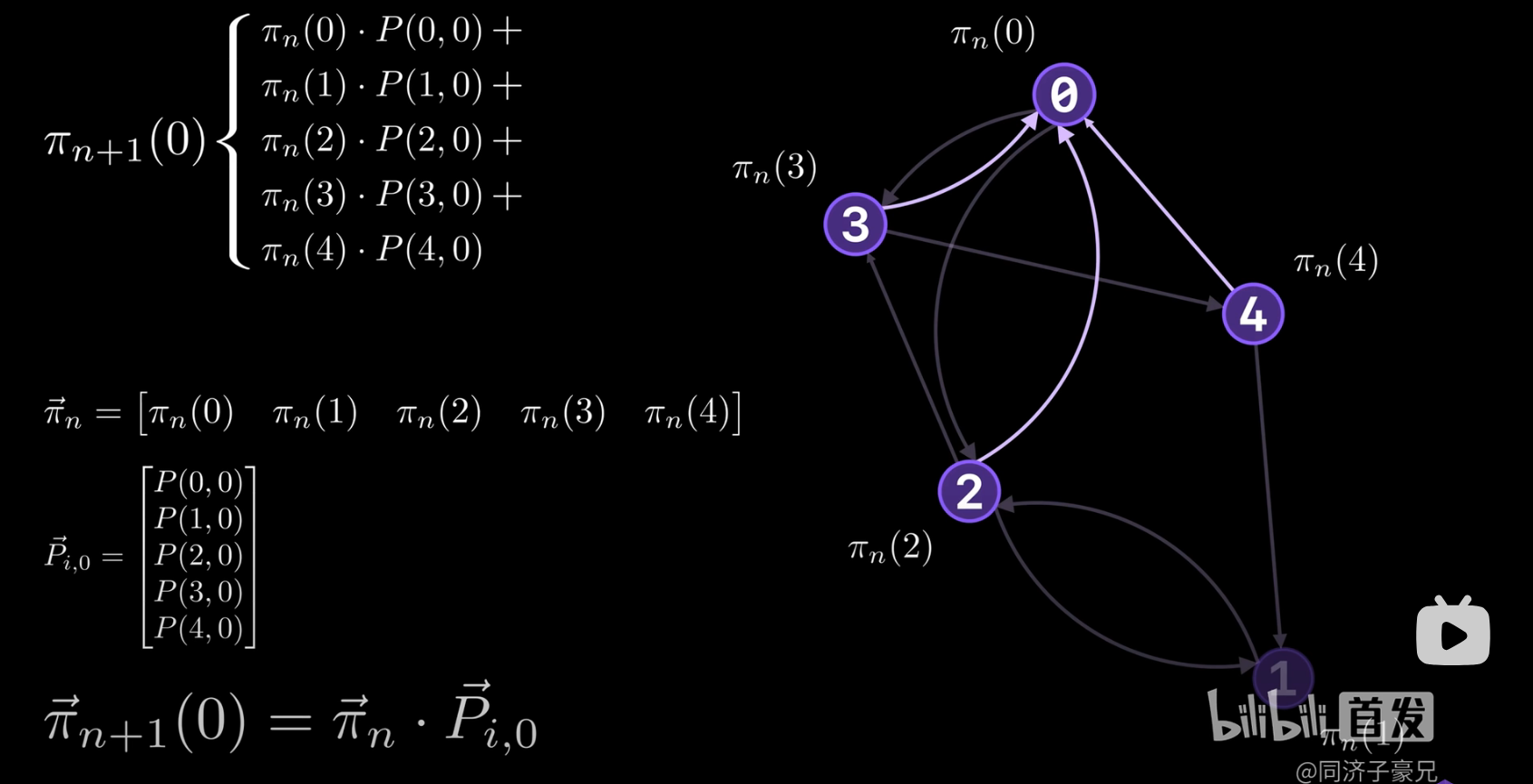
image.png

image.png

说明：图中的 Π n Π_n Πn?为n时刻的pagerank值，即状态概率分布， p i , 0 p_{i,0} pi,0?为从上一时刻各个状态转换到下一时刻0状态的概率分布

求解PageRank

选择方法：迭代左乘M矩阵，即幂迭代的方法
收敛判断： ∑ i ∣ r i t + 1 ? r i t ∣ < ? \sum_i|r_i^{t+1}-r_i^t| < \epsilon ∑i?∣rit+1??rit?∣<?

image.png

说明：这里的收敛判断使用的是 L 1 L_1 L1?范数，可以根据求解问题的不同更换，比如使用 L 2 L_2 L2?范数
一般而言，迭代50次左右就可以得到收敛结果

PageRank收敛性分析

解决以下四个问题

image.png

引入一个定理：irreducible和aperiodic的（不可约且非周期的）马尔可夫链就是收敛的，就能够解决前述的问题1和问题2

image.png

说明：irreducible的马尔科夫链即所有状态都是可达的，没有独立的完全不可达的状态存在

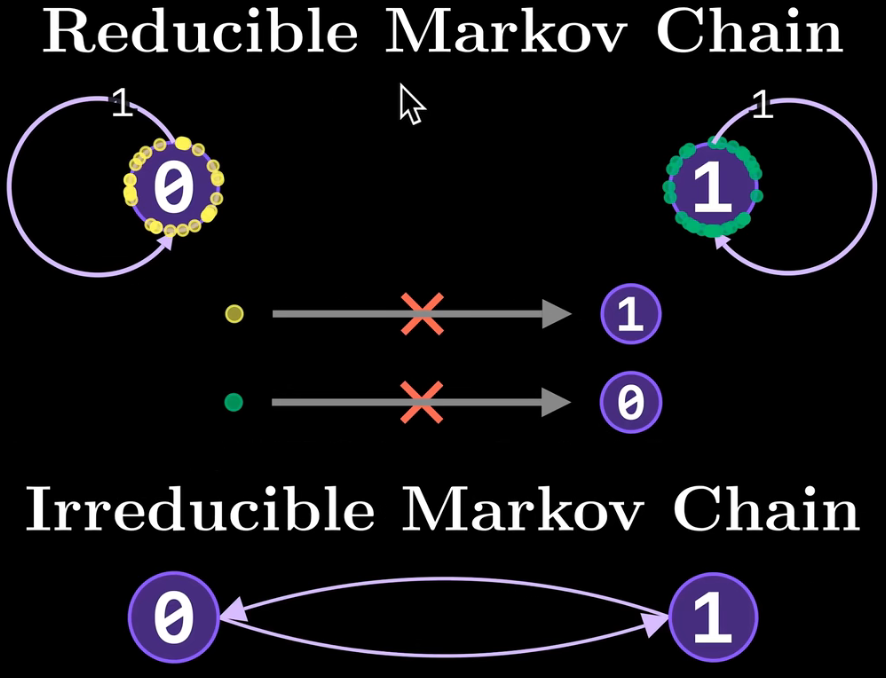
image.png

aperiodic的马尔可夫链即网络中不存在周期性震动的状态组

image.png

修改M得到G

网络中可能存在的问题

  1. spider traps：一个节点的只有指向自己的出链接
  2. dead ends： 一些节点没有出链接

spider traps示例：
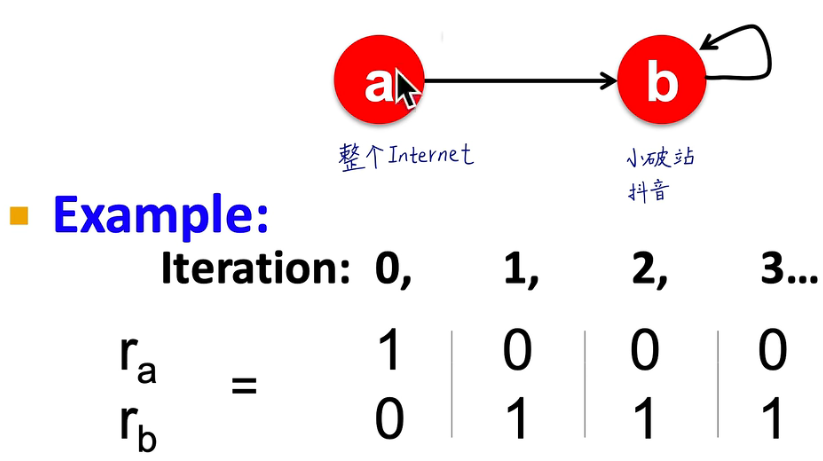
image.png

dead ends示例：违背了stochastic matrix的假设即所有列各个分量和为1
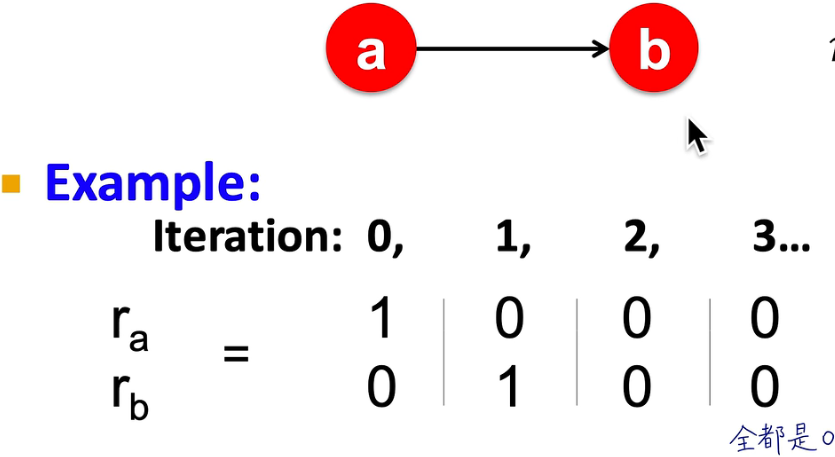
image.png

多个彼此独立的连通域
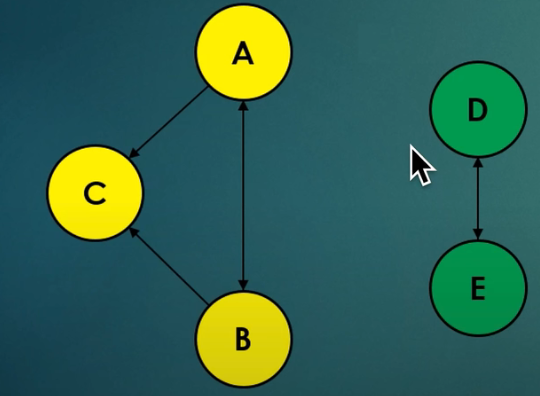
image.png

solution
处理spider traps和独立连通域问题——在t时刻到t+1时刻时，给一个概率 β \beta β surfer按照原来的出链接移动，(1- β \beta β )的概率被传送到一个随机节点
处理dead ends问题——在t时刻到t+1时刻时，surfer以概率为1的几率被传送到一个随机节点
归纳起来，解决这些问题都是通过改写M矩阵实现的
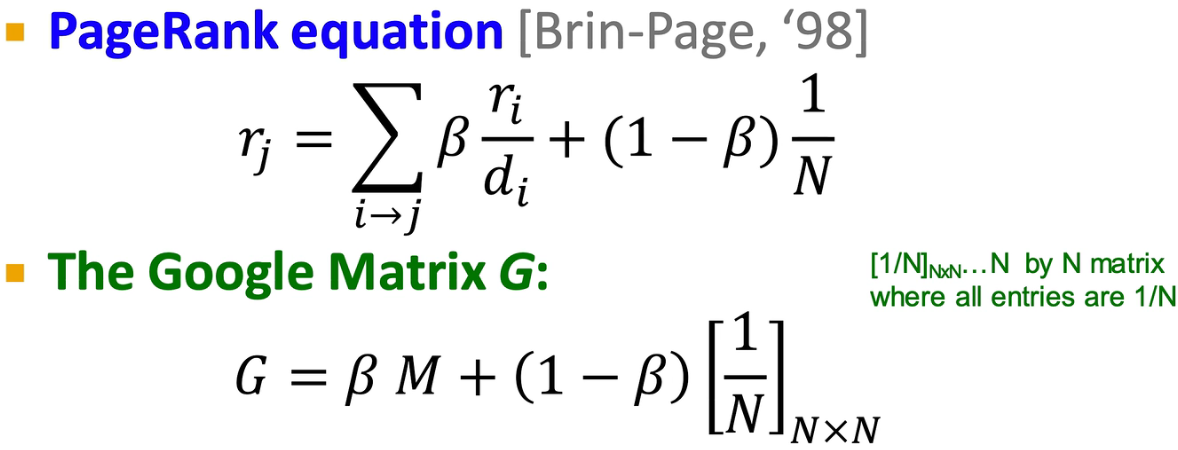
image.png
数学表示：
image.png

考虑节点相似度的PageRank算法

常用在推荐系统中
比如电商平台，将用户和商品作为图中两种节点，构成二部图，我们现在需要得到哪两种商品相似度高（背后的需求在于：若item A和item B相似度高，我们可以给购买了item A的用户推荐item B，反之同样适用），这里我们会假设说被同一用户购买的两种商品相似度是高的，或许还可以加上购买时间的考虑，称在同一时间段内被同一用户购买的两种商品是相似度高的

将节点相似度引入PageRank算法，修改了G矩阵中以1- β \beta β概率进行的随机游走情况
image.png

算法说明：选定目标节点，记为QUERY_NODES，模拟随机游走计数求和得到其他节点与目标节点的亲疏远近
image.png

伪代码展示：

ALPHA = 0.5
QUERY_NODES = {Q}
item = QUERY_NODES.sample_by_weight()
for i in range(N_STEPS):
	user = item.get_random_neighbor()
	item = user.get_random_neighbor()
	item.visit_count += 1
	if random() < ALPHA:
		item = QUERY_NODES.sample_by_weight()

参考资料

  1. 同济子豪兄课程repo地址：https://github.com/TommyZihao/zihao_course/tree/main/CS224W
文章来源:https://blog.csdn.net/m0_61819793/article/details/135544084
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章