Leetcoder Day2|有序数组的平方|长度最小的子数组 |螺旋矩阵II
语言:Java/C++
目录
977. 有序数组的平方
给你一个按非递减顺序排序的整数数组?
nums,返回每个数字的平方组成的新数组,要求也按?非递减顺序排序。
- 输入:nums = [-4,-1,0,3,10]
- 输出:[0,1,9,16,100]
- 输入:nums = [-7,-3,2,4]
- 输出:[4,9,9,16,49]
🏁?解题思路:
暴力解法
这道题首先是有序的,但并没有强调无重复,因此结合昨天的内容,不能一上来就想用二分查找法。按照暴力解法全部元素平方然后用sort函数直接可以AC,不过时间复杂度较高,因为sort函数的本质是快排算法,时间复杂度为O(nlogn),再加上一次for循环,所以暴力解法的整体.
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
for(int i=0; i<nums.size();i++){
nums[i]*=nums[i];
}
sort(nums.begin(),nums.end());
return nums;
}
};时间复杂度:O(n + nlogn)
双指针法
首先我们先看一下示例,可以看到,平方过后的数组中最大的元素一定是在当前平方前元素的两边之一,不是最左就是最右。因此可以设置左右双指针,从两边向中间依次遍历和比较。并且题目中没有强调原地,因此可以建立一个新的数组,设置一个索引k指向新数组最后一个元素,每次遇到当前最大的元素便赋值给当前k所指向的位置,然后k在新数组前移,最后返回新数组即可。过程如下:
①定义新数组,设置索引
②双指针移动比较
③寻找到最大的那一个数据存在新数组中
还要注意的一点是因为要考虑到左右两边的元素,因此最好采用左闭右闭的情况。
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
vector<int> result(nums.size(),0);//定义新数组
int k=nums.size()-1; //设置索引
for(int i=0, j=nums.size()-1;i<=j;){
if(nums[i]*nums[i]<nums[j]*nums[j]){
result[k]=nums[j]*nums[j];
j--;
}
else{
result[k]=nums[i]*nums[i];
i++;
}
k--;
}
return result;
}
};时间复杂度:O(n)
209.长度最小的子数组
给定一个含有?
n?个正整数的数组和一个正整数?target?。找出该数组中满足其总和大于等于?
target?的长度最小的?连续子数组?[numsl, numsl+1, ..., numsr-1, numsr]?,并返回其长度。如果不存在符合条件的子数组,返回?0?。
🌟 适用条件:与长度有关的,如一定长度内元素不重复或长度固定等,或窗元素和与某值有关,
🏁?解题思路:
滑动窗口
滑动窗口就是不断的调节子序列的起始位置和终止位置,从而得到想要的结果。本质上也是一种双指针法,不过和双指针的一个区别是,在移动终止位置的时,起始位置是不可逆的,只能向后移动。
因为本题除了要关注元素和以外,还有一个重要的点:长度,我们需要找出满足条件的且长度最小的连续数组并返回其长度。因此设立起始和终止两个指针,初始时同时指向第一个元素,将终止指针不断后移形成一个子数组即窗口,并计算窗口的元素和,若当前元素和大于等于target,说明已经达到了临界条件,将这个长度记录下来,然后将起始指针后移直到不满足临界条件(这里用while循环),终止指针继续后移,看是否有其他满足临界条件且长度更小的窗口。
理清滑动窗口的思路主要有以下三点:
- 窗口内是什么? 本题为满足其和 ≥ target的长度最小的连续子数组。
- 如何移动窗口的起始位置?当前窗口的值大于s了,窗口就要向前移动了
- 如何移动窗口的结束位置?窗口的结束位置不断向后移动即可
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int result=INT32_MAX;
int sum=0, sublength=0, i=0; //设置和,窗口初始大小和起始指针
for(int j=0;j<nums.size();j++){
sum+=nums[j];
while(sum>=target){
sublength=(j-i+1); //取窗口长度
result=result<sublength?result:sublength; //将更小的值赋给result
sum-=nums[i]; //将当前起始元素删除
i++; //起始位置后移
}
}
return result==INT32_MAX ? 0:result;
}
};- 时间复杂度:O(n)??每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)
- 空间复杂度:O(1)
59.螺旋矩阵II
给你一个正整数?
n?,生成一个包含?1?到?n2?所有元素,且元素按顺时针顺序螺旋排列的?n x n?正方形矩阵?matrix?。输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]] 输入:n = 1 输出:[[1]]
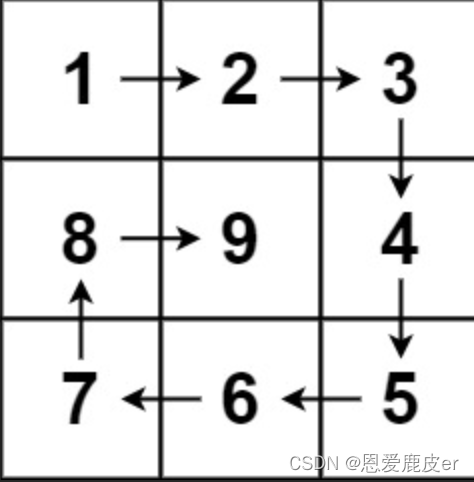
🏁?解题思路
每次一看到螺旋矩阵的问题,心里就会有点打怵,思路一直不是很清晰,因为数组在概念里一直是线性的,现在要变成一个非线形的情况,不是很有画面。还有一方面如卡哥所说边界条件的问题,写着写着就会蒙。要破解这个情况,需要谨记一点:坚持循环不变量原则,即一直坚持左闭右开或左开右闭的原则因此无论n是多少,这个题都变成了一个不断画四条边的问题。每次画完一圈,矩形的长度会减2,因此n/2为多少很关键。如果n为偶数,则循环n/2圈即可;如果n为奇数,则循环(n/2)+1圈,最后中间的位置为数组中最后一个数。过程如下:
- 初始化一个新的二维数组和起始位置,确定循环的圈数;
- 按照循环一致原则,从左到右,从上到下,从右到左,从下到上依次填充元素;
- 每循环完一圈,更新起始位置(均+1)并且控制边长(offset+1)
- 给n为奇数的中间位置赋值(最后一个元素)

class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n,0));//定义一个二维数组
int startx=0;
int starty=0, count=1, offset=1;//offset是控制边界的
int loop=n/2;
while(loop--){
int i = startx;
int j = starty;
for(j;j<n-offset;j++){//??从左往右的边
res[startx][j]=count++; //先赋值再加
}
for (i;i<n-offset;i++){//??从上往下的边
res[i][j]=count++;
}
for(;j>starty;j--){//从右往左的边
res[i][j]=count++;
}
for(;i>startx;i--){//从下往上的边
res[i][j]=count++;
}
//一圈结束后缩小所以起始位置要加1,边界也要在n的基础上缩小,offset加1
startx++;
starty++;
offset++;
}
if (n%2){
res[n/2][n/2]=count;
}
return res;
}
};- 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
- 空间复杂度 O(1)
最后附上Leetcode上本题第一的题解,来自Krahets,结合过程思路更清晰且代码简洁:
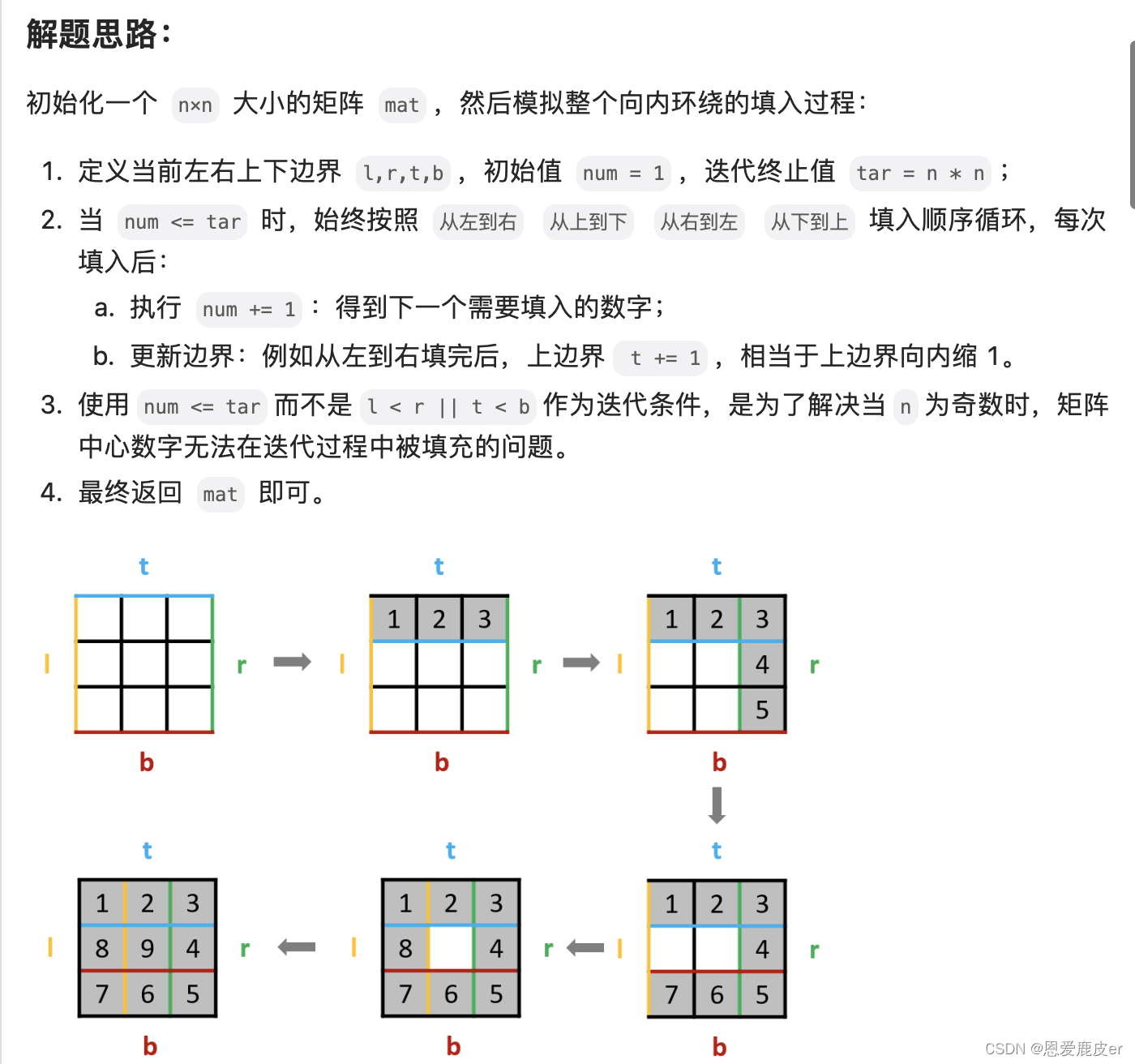
class Solution {
public int[][] generateMatrix(int n) {
int l = 0, r = n - 1, t = 0, b = n - 1;
int[][] mat = new int[n][n];
int num = 1, tar = n * n;
while(num <= tar){
for(int i = l; i <= r; i++) mat[t][i] = num++; // left to right.
t++;
for(int i = t; i <= b; i++) mat[i][r] = num++; // top to bottom.
r--;
for(int i = r; i >= l; i--) mat[b][i] = num++; // right to left.
b--;
for(int i = b; i >= t; i--) mat[i][l] = num++; // bottom to top.
l++;
}
return mat;
}
}
今日心得
今天三道题之前很久之前也都接触过,因此前两道题问题不大,第三道题通过看视频加上画图梳理,再一次捋清和明确了以后遇到这种矩阵问题的思路,肯定还要多刷几遍加强熟练度的。加上写博客总用时一个半小时,继续努力💪。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- unity中旋转 transform.Rotate
- 四、C++运算符(4)比较运算符
- I2C总线协议工作原理简述
- 第4课 FFmpeg读取本地mp4文件并显示
- 相关分析和回归分析的联系和区别(自用)
- 爬虫工作量由小到大的思维转变---<第二十二章 Scrapy开始很快,越来越慢(诊断篇)>
- 【HarmonyOS】【DevEco Studio】安装教程及环境配置问题解决
- AJAX(一)
- SERVLET的概念
- 基于51单片机的智能水表电路设计