面试算法115：重建序列

题目

长度为n的数组org是数字1～n的一个排列，seqs是若干序列，请判断数组org是否为可以由seqs重建的唯一序列。重建的序列是指seqs所有序列的最短公共超序列，即seqs中的任意序列都是该序列的子序列。
例如，如果数组org为[4，1，5，2，6，3]，而seqs为[[5，2，6，3]，[4，1，5，2]]，因为用[[5，2，6，3]，[4，1，5，2]]可以重建出唯一的序列[4，1，5，2，6，3]，所以返回true。如果数组org为[1，2，3]，而seqs为[[1，2]，[1，3]]，因为用[[1，2]，[1，3]]可以重建出两个序列，[1，2，3]或[1，3，2]，所以返回false。

分析

超序列和子序列是两个相对的概念。如果序列A中的所有元素按照先后顺序都在序列B中出现，那么序列A是序列B的子序列，序列B是序列A的超序列。

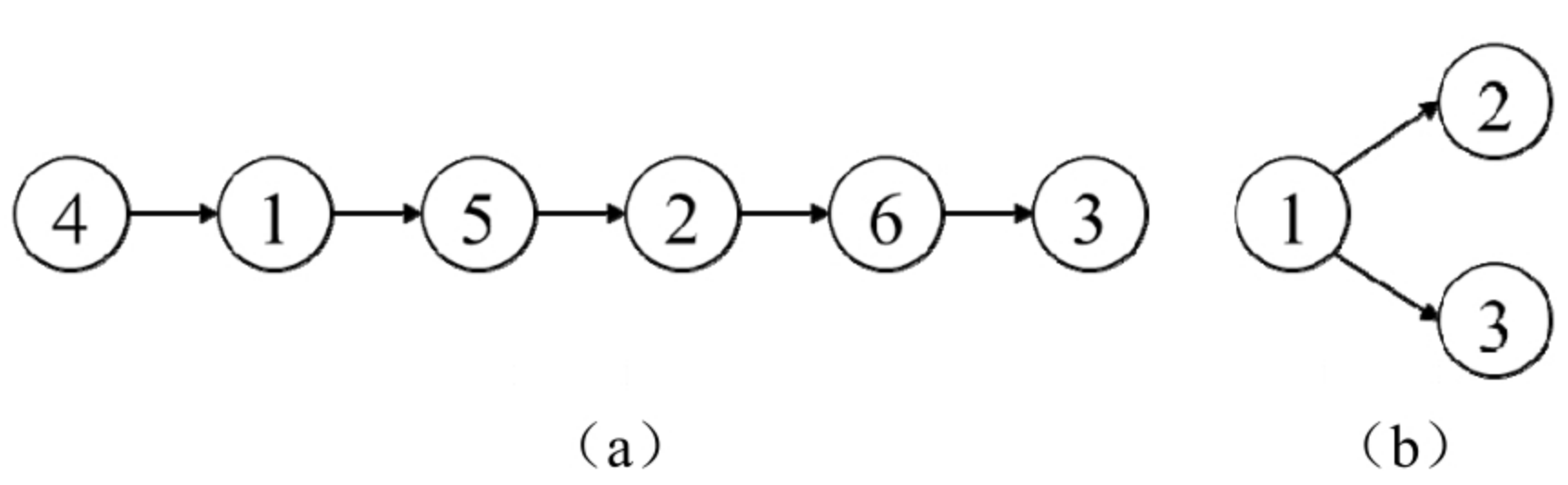
如果得到的是有向图的拓扑排序序列，那么任意一条边的起始节点在拓扑排序序列中一定位于终止节点的前面。因此，由seqs重建的序列就是由seqs构建的有向图的拓扑排序的序列。这个问题就转变成判断一个有向图的拓扑排序序列是否唯一。

解

public class Test {
    public static void main(String[] args) {
        int[] org = {4, 1, 5, 2, 6, 3};
        List<Integer> list1 = Arrays.asList(5, 2, 6, 3);
        List<Integer> list2 = Arrays.asList(4, 1, 5, 2);
        List<List<Integer>> seqs = Arrays.asList(list1, list2);
        boolean result = sequenceReconstruction(org, seqs);
        System.out.println(result);
    }

    public static boolean sequenceReconstruction(int[] org, List<List<Integer>> seqs) {
        Map<Integer, Set<Integer>> graph = new HashMap<>();
        Map<Integer, Integer> inDegrees = new HashMap<>();
        for (List<Integer> seg : seqs) {
            for (int num : seg) {
                if (num < 1 || num > org.length) {
                    return false;
                }

                graph.putIfAbsent(num, new HashSet<>());
                inDegrees.putIfAbsent(num, 0);
            }
            for (int i = 0; i < seg.size() - 1; i++) {
                int num1 = seg.get(i);
                int num2 = seg.get(i + 1);
                if (!graph.get(num1).contains(num2)) {
                    graph.get(num1).add(num2);
                    inDegrees.put(num2, inDegrees.get(num2) + 1);
                }
            }
        }

        Queue<Integer> queue = new LinkedList<>();
        for (int num : inDegrees.keySet()) {
            if (inDegrees.get(num) == 0) {
                queue.add(num);
            }
        }

        Queue<Integer> built = new LinkedList<>();
        while (queue.size() == 1) {
            int num = queue.remove();
            built.add(num);
            for (int next : graph.get(num)) {
                inDegrees.put(next, inDegrees.get(next) - 1);
                if (inDegrees.get(next) == 0) {
                    queue.add(next);
                }
            }
        }

        int[] result = new int[built.size()];
        result = built.stream().mapToInt(i -> i).toArray();
        return Arrays.equals(result, org);
    }

}