LeetCode每日一题——2132.用邮票贴满网格图

参考资料：

• 2132. 用邮票贴满网格图 - 力扣（LeetCode）

题目描述

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

1. 覆盖所有 空 格子。
2. 不覆盖任何 被占据 的格子。
3. 我们可以放入任意数目的邮票。
4. 邮票可以相互有 重叠 部分。
5. 邮票不允许 旋转 。
6. 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

样例

思路

主要思想：二维前缀和 + 二维差分

由于题目没有限制放入邮票的数量，也允许邮票相互重叠，所以我们应该尽可能地多贴邮票。

假设我们以邮票的左上角 (i,j)为基准粘贴邮票，则该邮票的覆盖范围是 (i.j) ~ (x,y) ，其中 x = i+stampHeight-1, y = j+stampHeight-1。为了铺满整张网格图，我们遍历每个格子，判断能否以当前格子为左上角粘贴邮票，最后，我们检查是否每个空格子都被邮票覆盖即可。关键问题在于：

1. 如果快速判断一个矩形范围 (i.j) ~ (x,y) 内是否存在被占据的格子。
2. 在贴上邮票后如何更新矩阵的状态，并在最后快速判断每个空格子是否被覆盖。

对于第一个问题，我们可以使用二维前缀和解决。定义 sum[i][j] 表示范围 (0,0) ~ (i,j) 内被占据格子的数量，那么对与我们要粘贴邮票的范围 (i.j) ~ (x,y) ，只需判断 sum[x][y]-sum[i-1][y]-sum[x][j-1]+sum[i-1][j-1] 是否为 0 即可。

对于第二个问题，我们可以使用二维差分解决。由于本人之前对于差分的理解不是很到位，所以这里展开说一下。差分可以看作前缀和的逆运算，我们对差分数组求前缀和即可得到原数组，对原数组求前缀和即可得到前缀和数组。假设这里的原数组 arr[i][j] 表示当前格子上的邮票数量，那差分数组 diff 就应该按照下图方式修改：

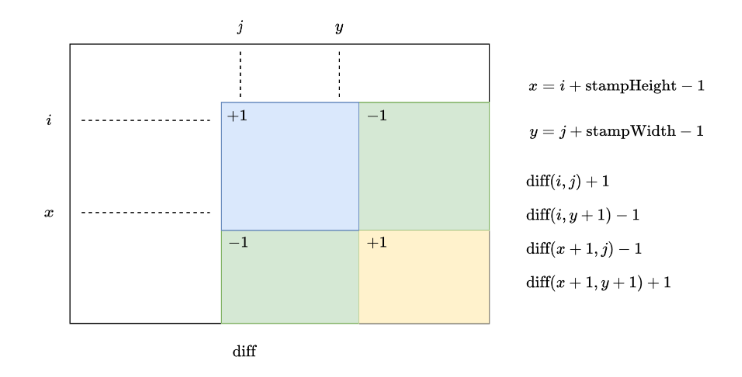
代码

不得不承认，我求二维前缀和、二维差分的代码极其丑陋。。。

class Solution {
public:
    bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> sum(grid.begin(), grid.end());
        vector<vector<int>> diff(m, vector<int>(n, 0));
        for(int i=0;i<m;++i){
            for(int j=1;j<n;++j){
                sum[i][j] += sum[i][j-1];
            }
        }
        for(int i=1;i<m;++i){
            for(int j=0;j<n;++j){
                sum[i][j] += sum[i-1][j];
            }
        }
        for(int i=0;i<m;++i){
            for(int j=0;j<n;++j){
                if(grid[i][j]) continue;
                int x = i+stampHeight-1, y = j+stampWidth-1;
                if(x>=m || y>=n) continue;
                int temp = sum[x][y];
                if(i>0) temp -= sum[i-1][y];
                if(j>0) temp -= sum[x][j-1];
                if(i>0 && j>0) temp += sum[i-1][j-1];
                if(temp == 0){
                    ++diff[i][j];
                    if(x+1<m) --diff[x+1][j];
                    if(y+1<n) --diff[i][y+1];
                    if(x+1<m && y+1<n) ++diff[x+1][y+1];
                }
            }
        }
        for(int i=0;i<m;++i){
            for(int j=1;j<n;++j){
                diff[i][j] += diff[i][j-1];
            }
        }
        for(int i=1;i<m;++i){
            for(int j=0;j<n;++j){
                diff[i][j] += diff[i-1][j];
            }
        }
        for(int i=0;i<m;++i){
            for(int j=0;j<n;++j){
                if(!grid[i][j] && !diff[i][j]) return false;
            }
        }
        return true;
    }
};