【小呆的力学笔记】弹塑性力学的初步认知二：应力应变分析(2)

1.4 主应力空间、八面体应力

一点的应力状态不论如何变化，其主应力和主方向一致的话，该点的应力状态就是唯一确定的。因此，我们用主应力方向建立一个三维坐标系来描述问题将不失一般性，该坐标系如下图4，我们称之为主应力空间。我们考察等倾面组成的八面体，图中O’P点为等倾面ABC上面的应力向量$(p_1,p_2,p_3)$，八面体为等倾面八面体，即面ABC的法线方向余弦为$(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}})$。将O’P分解
$$\overline{O’P}=\overline{O’Q}+\overline{O’N}\text{\hspace{1em}(25)}$$

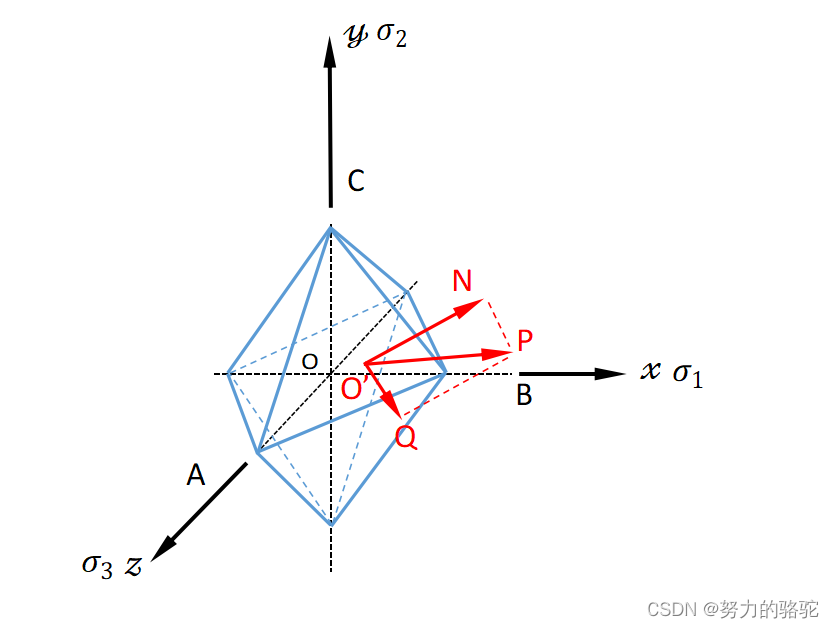
$$图4八面体$$
取等倾面和三个轴的坐标面组成的四面体为研究对象，如下图5所示。

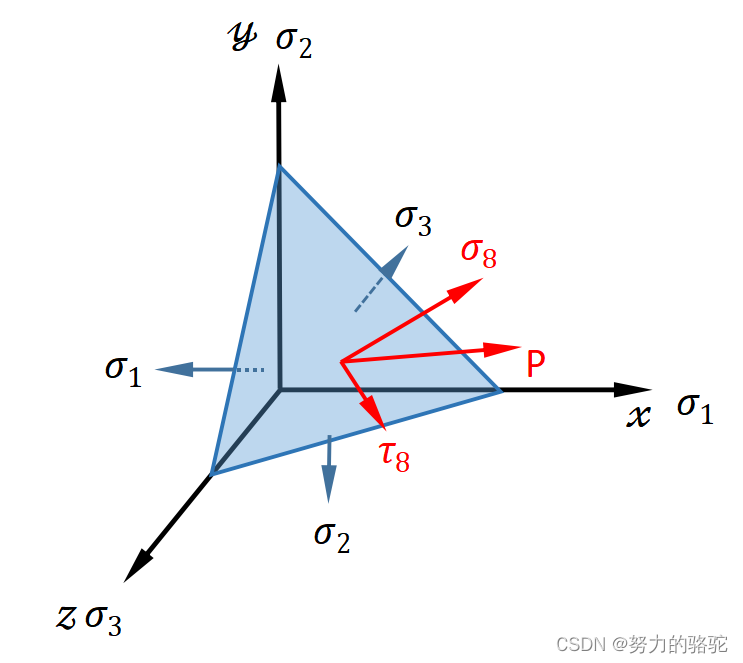
$$图5等倾面四面体$$
根据斜面应力公式$p_j={\sigma }_{ij}{n}_i$，不难得到以下关系式（矩阵形式）
$$\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]=\left[\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_2\end{array}\right]\left[\begin{array}{c}{n}_1\\ n_2\\ n_3\end{array}\right]\text{\hspace{1em}(26)}$$

其中$(n_1,n_2,n_3)=(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}})$为等倾面的法线方向余弦。
那么，有
$${\sigma }_8=\left[\begin{array}{ccc}{n}_1& n_2& n_3\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]={\sigma }_1{n}_1^2+{\sigma }_2{n}_2^2+{\sigma }_3{n}_3^2=\frac{1}{3}({\sigma }_1+{\sigma }_2+{\sigma }_3)=\frac{1}{3}{I}_1\text{\hspace{1em}(27)}$$
八面体相应的剪应力为
$$\begin{gathered} {\tau }_8=\sqrt{p^2?{\sigma }_8^2}=\sqrt{p_1^2+p_2^2+p_3^2?({\sigma }_1{n}_1^2+{\sigma }_2{n}_2^2+{\sigma }_3{n}_3^2{)}^2} \\ =\sqrt{{\sigma }_1^2{n}_1^2+{\sigma }_2^2{n}_2^2+{\sigma }_3^2{n}_3^2?({\sigma }_1{n}_1^2+{\sigma }_2{n}_2^2+{\sigma }_3{n}_3^2{)}^2} \\ =\sqrt{\frac{1}{3}({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2)?\frac{1}{9}({\sigma }_1+{\sigma }_2+{\sigma }_3{)}^2} \\ =\frac{1}{3}\sqrt{3({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2)?({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2+2{\sigma }_1{\sigma }_2+2{\sigma }_1{\sigma }_3+2{\sigma }_2{\sigma }_3)} \\ =\frac{1}{3}\sqrt{({\sigma }_1?{\sigma }_2{)}^2+({\sigma }_1?{\sigma }_3{)}^2+({\sigma }_2?{\sigma }_3{)}^2}=\sqrt{\frac{2}{3}{J}_2}=\sqrt{\frac{1}{3}{s}_{ij}{s}_{ij}}\text{\hspace{1em}(28)} \end{gathered}$$

1.5 应变分析

应变分析的内容同应力分析内容，只是注意一点，应变张量和工程应变在剪应变分量是不同的，定义如下。
$$\left[\begin{array}{ccc}{\epsilon }_{xx}& {\epsilon }_{yx}& {\epsilon }_{zx}\\ {\epsilon }_{xy}& {\epsilon }_{yy}& {\epsilon }_{zy}\\ {\epsilon }_{xz}& {\epsilon }_{yz}& {\epsilon }_{zz}\end{array}\right]=\left[\begin{array}{ccc}{\epsilon }_{xx}& \frac{1}{2}{\gamma }_{yx}& \frac{1}{2}{\gamma }_{zx}\\ \frac{1}{2}{\gamma }_{xy}& {\epsilon }_{yy}& \frac{1}{2}{\gamma }_{zy}\\ \frac{1}{2}{\gamma }_{xz}& \frac{1}{2}{\gamma }_{yz}& {\epsilon }_{zz}\end{array}\right]\text{\hspace{1em}(29)}$$
同样定义应变偏张量，有如下形式
$$\left[\begin{array}{ccc}{e}_{xx}& e_{yx}& e_{zx}\\ e_{xy}& e_{yy}& e_{zy}\\ e_{xz}& e_{yz}& e_{zz}\end{array}\right]=\left[\begin{array}{ccc}{\epsilon }_{xx}& {\epsilon }_{yx}& {\epsilon }_{zx}\\ {\epsilon }_{xy}& {\epsilon }_{yy}& {\epsilon }_{zy}\\ {\epsilon }_{xz}& {\epsilon }_{yz}& {\epsilon }_{zz}\end{array}\right]?\left[\begin{array}{ccc}{\epsilon }_m& 0& 0\\ 0& {\epsilon }_m& 0\\ 0& 0& {\epsilon }_m\end{array}\right]\text{\hspace{1em}(30)}$$
其中${\epsilon }_m=\frac{1}{3}({\epsilon }_{xx}+{\epsilon }_{yy}+{\epsilon }_{zz})$

1.6 特殊应力、应变定义

定义应力强度或等效应力$\overline{\sigma }$为
$$\begin{gathered} \overline{\sigma }=\sqrt{3J_2}=\sqrt{\frac{3}{2}{s}_{ij}{s}_{ij}} \\ =\sqrt{\frac{1}{2}[({\sigma }_1?{\sigma }_2{)}^2+({\sigma }_1?{\sigma }_3{)}^2+({\sigma }_2?{\sigma }_3{)}^2]} \\ =\sqrt{\frac{1}{2}[({\sigma }_{xx}?{\sigma }_{yy}{)}^2+({\sigma }_{xx}?{\sigma }_{zz}{)}^2+({\sigma }_{yy}?{\sigma }_{zz}{)}^2+6({\tau }_{xz}^2+{\tau }_{xy}^2+{\tau }_{yz}^2)]}\text{\hspace{1em}(31)} \end{gathered}$$
定义应变强度或等效应变$\overline{\epsilon }$为
$$\overline{\epsilon }=\sqrt{\frac{2}{3}{e}_{ij}{e}_{ij}}\text{\hspace{1em}(32)}$$

定义剪切等效应力$\overline{T}$为
$$\overline{T}=\sqrt{\frac{1}{2}{s}_{ij}{s}_{ij}}\text{\hspace{1em}(33)}$$
定义剪切等效应变$\overline{\Gamma }$为
$$\overline{\Gamma }=\sqrt{2e_{ij}{e}_{ij}}\text{\hspace{1em}(34)}$$
加上上面定义的八面体剪应力、八面体剪应变
$$\begin{gathered} {\tau }_8=\sqrt{\frac{1}{3}{s}_{ij}{s}_{ij}} \\ {\gamma }_8=\sqrt{\frac{4}{3}{e}_{ij}{e}_{ij}}\text{\hspace{1em}(35)} \end{gathered}$$

至于为什么定义这些应力应变，我们在后面再介绍。